6.5: La aproximación de unión apretada

Cada átomo en un conductor típicamente posee muchos electrones. Podemos simplificar significativamente los cálculos orbitales moleculares al descuidar todos menos algunos de los electrones. La base para discriminar entre los electrones es la energía. Los electrones ocupan diferentes orbitales atómicos: algunos electrones requieren mucha energía para ser sacados del átomo, y otros están más débilmente ligados.

Nuestra primera suposición es que los electrones en los orbitales atómicos profundos no participan en el transporte de carga. Recordemos que la conducción de carga solo ocurre a través de estados cercanos al nivel Fermi. Así, nos preocupa sólo los electrones más débilmente ligados que ocupen los llamados orbitales atómicos fronterizos.

En esta clase, consideraremos exclusivamente materiales a base de carbono. Además, solo consideraremos carbono en la geometría triangular que produce orbitales atómicos\(sp^{2}\) hibridados; ver Apéndice 4 para una discusión completa. En estos materiales, cada átomo de carbono tiene un electrón en un\(p_{z}\) orbital no hibridado. El orbital\(p_{z}\) atómico no hibridado es el orbital fronterizo. Es el más débilmente unido y también contribuye a orbitales\(\pi\) moleculares que proporcionan una ruta de conducción conveniente para los electrones a lo largo de la molécula. Supondremos que los orbitales moleculares del conductor relevantes para el transporte de carga son combinaciones lineales de orbitales atómicos fronterizos.

Por ejemplo, consideremos el átomo de carbono central en la Figura 6.6.1. Supongamos que el átomo es parte de una red triangular y que en consecuencia contiene un electrón en un orbital\(p_{z}\) atómico fronterizo. Consideremos el efecto del átomo de carbono vecino a la derecha del átomo central.

Figura\(\PageIndex{1}\): Un átomo de carbono con un solo electrón fronterizo y su núcleo vecino. El hamiltoniano del sistema contiene términos potenciales para cada uno de los dos núcleos.

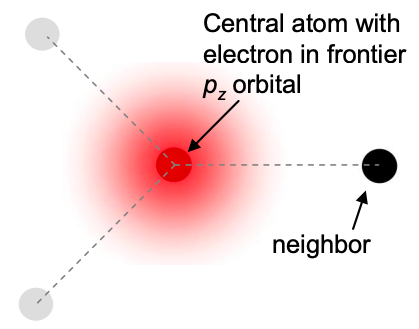
Suponiendo que las posiciones de los átomos son fijas, el hamiltoniano del sistema consiste en un operador de energía cinética, y dos términos de potencial coulómbico: uno para el átomo central y otro para su vecino:

\[ H = T + V_{1} + V_{2} \nonumber \]

Ahora, considere una integral de la forma:

\[ \left< \phi_{r} | H | \psi \right> \left< \phi_{r} | E | \psi \right> \nonumber \]

Siguiendo la Ecuación (6.4.1), la función de onda en este sistema de dos átomos puede escribirse como

\[ \psi = c_{1}\phi_{1}+c_{2}\phi_{2} \nonumber \]

Podemos ampliar el LHS de la Ec. (6.6.2) de la siguiente manera:

\[ \left< \phi_{r}|H|\psi \right> = c_{1}\left< \phi_{r}|T+V_{1}|\phi_{1} \right> + c_{1}\left< \phi_{r}|V_{2}|\phi_{1} \right> + c_{2}\left< \phi_{r}|T+V_{2}|\phi_{2} \right> + c_{2}\left< \phi_{r}|V_{1}|\phi_{2} \right> \nonumber \]

El RHS se expande a medida que

\[ \left< \phi_{r}|E|\psi \right> = c_{1}E\left< \phi_{r}|\phi_{1} \right> + c_{2}E\left< \phi_{r}|\phi_{2} \right> \nonumber \]

Los términos en estas expansiones no son igualmente importantes. Podemos simplificar considerablemente el cálculo categorizando las diversas interacciones e ignorando las menos importantes.

Integrales solapadas

En primer lugar, definamos la integral de superposición entre los orbitales fronterizos en los sitios atómicos s y r:

\[ S_{sr} = \left< \phi_{s}|\phi_{r} \right> \nonumber \]

Estas integrales producen el solapamiento entre orbitales atómicos en diferentes sitios en el sólido. La separación espacial generalmente asegura que\(S_{sr} \ll 1\) para\(s \neq r\). Por supuesto, para orbitales atómicos normalizados\(S_{sr} = 1\) para\(s = r\).

Figura\(\PageIndex{2}\): El solapamiento entre dos orbitales atómicos adyacentes está sombreado en amarillo. En la aproximación de unión apretada asumiremos que el solapamiento entre orbitales atómicos fronterizos en diferentes sitios es cero.

La autoenergía

A continuación, definamos la autoenergía. En un sitio atómico particular, tenemos

\[ T+V_{r}|\phi_{r}\big \rangle = \alpha_{r}|\phi_{r}\big \rangle \nonumber \]

donde\(\alpha_{r}\) está la energía del uno mismo, es decir:

\[ \alpha_{r}= \left< \phi_{r}|T+V_{r}|\phi_{r}\right> \nonumber \]

La autoenergía,\(\alpha\), se define como negativa para un electrón en un potencial nuclear de carga positiva. Tenga en cuenta que si la interacción entre los átomos es débil entonces la autoenergía es similar a la energía, E, del sistema combinado.

Figura\(\PageIndex{3}\): La interacción entre un núcleo y su órbita atómica fronteriza se conoce como la autoenergía.

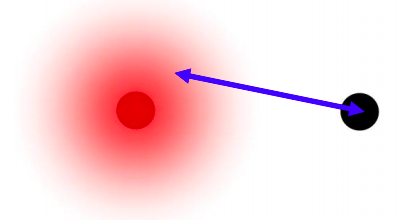
Interacciones de salto

Definamos la interacción de salto entre diferentes sitios s y r:

\[ \beta_{sr} = \left< \phi_{s}|V_{s}|\phi_{r} \right> \nonumber \]

La interacción de salto,\(\beta\), se define como negativa para un electrón en un potencial nuclear de carga positiva.

Figura\(\PageIndex{4}\): La interacción entre un núcleo y la órbita atómica fronteriza vecina se conoce como la interacción de salto.

Las interacciones restantes

La interacción restante considera la interacción de una órbita fronteriza en un sitio con el potencial en otro sitio. Tiene la forma

\[ \left< \phi_{r}|V_{s}|\phi_{r} \right> \nonumber \]

donde\(s \neq r\). Puede que no sea inmediatamente evidente que esta interacción suele ser mucho más débil que la interacción de salto de la Ecuación (6.6.9). Pero si los orbitales fronterizos individuales decaen exponencialmente con la distancia como exp [- ka] donde a es el espaciamiento entre los átomos, entonces estos términos se comportan como exp [-2 ka] mientras que el término de salto y solapamiento integral\(S_{sr}\) para\(s \neq r\) ambos siguen exp [- ka ].

En consecuencia, vamos a descuidar esta interacción.

Así, la Ecuación (6.6.2) se puede reescribir para r = 1 y r = 2 como

\[ c_{1}\alpha_{1}+c_{2}\beta_{12}+c_{2}\alpha_{2}S_{12} = c_{1}E+c_{2}ES_{12} \nonumber \]

\( c_{2}\beta_{21}+c_{1}\alpha_{1}S_{21}+c_{2}\alpha_{2} = c_{1}ES_{21}+c_{2}E \)

Los términos que contienen solo la autoenergía o energía, E, del sistema combinado son grandes. Los términos pequeños se destacan a continuación en rojo:

\[ c_{1}\alpha_{1}+\textcolor{red}{c_{2}\beta_{12}}+\textcolor{red}{c_{2}(\alpha_{2}-E)S_{12}} = c_{1}E \nonumber \]

\( \textcolor{red}{c_{1}\beta_{21}}+\textcolor{red}{c_{1}(\alpha_{1}-E)S_{21}} + c_{2}\alpha_{2} = c_{2}E \)

A continuación, observamos que la diferencia entre las autoenergías\(\alpha_{2}\),\(\alpha_{1}\) y, y la energía, E, del sistema combinado puede ser pequeña. Bajo este límite, podemos reducir aún más las ecuaciones a

\ [c_ {1}\ alfa_ {1} + c_ {2}\ beta_ {12} = c_ {1} E\\
c_ {1}\ beta_ {21} +c_ {2}\ alfa_ {2} = c_ {2} E\ nonumber\]

Escrito como una matriz, obtenemos

\ [\ left (\ begin {array} {ll}
\ alpha_ {1} &\ beta_ {12}\
\ beta_ {21} &\ alpha_ {2}
\ end {array}\ right)\ left (\ begin {array} {l}
c_ {1}\
c_ {2}
\ end {array}\ right) =E\ left (\ begin {array} {l}
c_ {1}\\
c_ {2}
\ end {array}\ derecha)\ nonumber\]

Así, podemos ignorar las integrales solapadas de los átomos separados.

En resumen, la teoría de la unión apretada hace las siguientes aproximaciones:

1. Considere solo orbitales atómicos fronterizos
2. Considerar solo las interacciones entre los orbitales atómicos fronterizos de los vecinos más cercanos. Esta es la aproximación de unión apretada.
3. Ignorar las integrales solapadas de los átomos separados, i.e\(S_{sr} = \delta_{sr}\). Esto es válido sólo cuando\(\alpha_{1} \approx \alpha_{2} \approx E\). Supondremos\(S_{sr} = \delta_{sr}\) generalmente para simplificar las matemáticas.

La autoenergía\(\alpha\), y la interacción de salto\(\beta\), podrían calcularse numéricamente dado el potencial y la órbita atómica fronteriza. Pero, en esta clase, en realidad no vamos a determinar\(\alpha\) y\(\beta\). Más bien nos interesa la forma de las funciones de onda molecular y las relaciones de dispersión para sus energías. Con esta información podemos determinar si el conductor es un metal o un aislante, y su densidad de estados.