6.14: Funciones Bloch- funciones de onda en moléculas periódicas

Las funciones de Bloch describen las funciones de Onda en materiales periódicos. Para entender mejor sus propiedades, es instructivo para nosotros derivar funciones de Bloch. \(^{†}\)

Primero, consideremos una molécula periódica, compuesta por células unitarias traducidas por múltiplos de los vectores primitivos de celosía. Deje que sea la función de onda de la celda unitaria\(\phi_{0}\). Bajo la aproximación de unión estrecha, la función de onda de la celda unitaria se construye a partir de una combinación lineal de orbitales atómicos fronterizos.

Figura\(\PageIndex{1}\): Los orbitales moleculares de moléculas periódicas son combinaciones lineales de las funciones de onda de las células unitarias.

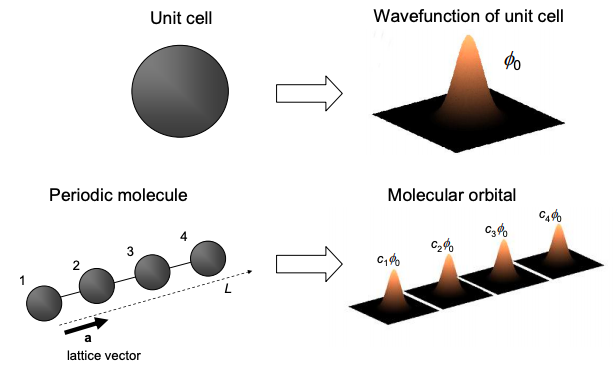
Ahora, los orbitales moleculares estarán compuestos por combinaciones lineales de la función de onda de la célula unitaria, i.e.

\[ \Psi = \sum_{r} c_{r}\phi_{0} \nonumber \]

donde una vez más\(c_{r}\) es un conjunto de coeficientes. Nótese que, a diferencia de las aproximaciones de orbitales moleculares que utilizan combinaciones lineales de orbitales atómicos fronterizos, la Ecuación (6.15.1) es exacta. Destacamos que\(\phi_{0}\) en la Ecuación (6.15.1) se encuentra la función de onda exacta de una célula unitaria de la molécula completa. En los cálculos orbitales moleculares\(\phi_{0}\) se calcula típicamente usando unión apretada, u otra técnica aproximada. Pero por el momento vamos a suponer que lo conocemos exactamente.

El objetivo de esta derivación es determinar los coeficientes cr dado que el material es periódico. En general, podemos relacionar los dos coeficientes\(c_{1}\) y\(c_{2}\) de las dos primeras celdas unitarias por

\[ c_{2} =\alpha c_{1} \nonumber \]

donde\(\alpha\) hay alguna constante.

La simetría del material nos permite traducir indistinguiblemente y consecuentemente,

\[ c_{r+1} =\alpha c_{r} \nonumber \]

donde 0 < r < N, donde N es el número de celdas unitarias en el material.

Ahora bien, si asumimos condiciones de límite periódicas, podemos comparar las celdas unitarias idénticas en r y r + N:

Figura\(\PageIndex{2}\): Aplicación de condiciones de límite periódicas a una molécula ya periódica.

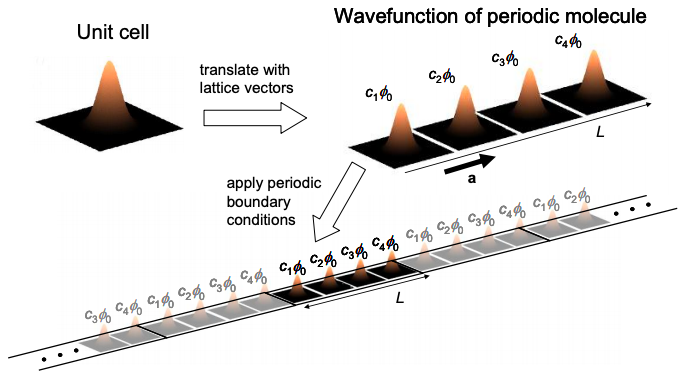
\[ c_{N+1} =\alpha^{N} c_{1} \nonumber \]

Pero ya que\(c_{N+1} = c_{1}\),\(\alpha\) debe ser una de N raíces de unidad, es decir\(\alpha = \text{exp}[i2\pi n/N]\), donde n es un entero. Así, los coeficientes son factores de fase; la función de onda correspondiente a cada célula unitaria es modulada por un factor de fase en una molécula periódica. En consecuencia, si establecemos\(c_{N} = 1\) (lo que podemos hacer ya que la fase absoluta es arbitraria):

\[ c_{r}=e^{i\frac{2\pi n}{N}r} \nonumber \]

Como alternativa, aproximando los coeficientes mediante una función continua, podemos escribir:

\[ c(x)=e^{ikx} \nonumber \]

donde

\[ \frac{2\pi n}{L} \nonumber \]

Una vez más, solo ciertos valores k son permitidos por la aplicación de condiciones de contorno periódicas. Después de todo, las ondas estacionarias en la molécula solo pueden poseer ciertas longitudes de onda. Recordemos también que las transformadas de Fourier de señales periódicas son discretas; ver Figura 6.16.1. Así, de un análisis de Fourier de los coeficientes se desprende que k debe ser discreto. Además, la transformada de Fourier de los coeficientes es en sí misma periódica ya que los coeficientes son discretos (recordar series discretas de Fourier de tiempo - DTFS).

\(^{†}\)Nuestro método sigue la derivación de Kittel en “Introducción a la Física del Estado Sólido”, Wiley, 7a Edición, 1996.