6.23: Problemas
- Page ID
- 84218
1. Considere la interacción de dos átomos de carbono cada uno con un electrón en un orbital\(2p_{z}\) atómico fronterizo. Suponiendo que las posiciones de los átomos son fijas, el hamiltoniano del sistema consiste en un operador de energía cinética, y dos términos de potencial coulómbico: uno para el átomo central y otro para su vecino:
\( H=T+V_{1}+V_{2} \)
Supongamos que la función de onda en este sistema de dos átomos puede escribirse como
\( \psi = c_{1}\phi_{1}+c_{2}\phi_{2} \)
donde\(\phi_{1}\) y\(\phi_{2}\) son los orbitales\(2p_{z}\) atómicos en el primer y segundo átomos de carbono, respectivamente,\(c_{1}\) y y\(c_{2}\) son constantes.
La autoenergía se define como
\( \alpha_{r} = \left< \phi_{r}| T+V_{r} |\phi_{r} \right> \)
Las interacciones de salto se definen como
\( \beta_{sr} = \left< \phi_{s}| V_{s} |\phi_{r} \right> \)
Anteriormente, asumimos que la integral de superposición entre los orbitales fronterizos en los sitios atómicos s y r podría aproximarse como
\( S_{sr} = \left< \phi_{s}|\phi_{r} \right> = \delta_{sr} \)
No hagas esa suposición aquí y demuestres que las energías electrónicas del sistema satisfacen
\[ \det (H - ES) = 0 \nonumber \]
donde H es una matriz hamiltoniana 2×2 y S es una matriz de superposición 2×2 y E es una constante.
(a) Escribir cada matriz en la Ecuación (6.24.1) en términos de las energías propias, integrales de salto e integrales superpuestas.
(b) ¿En qué condiciones puede ignorar con seguridad las integrales superpuestas?
2.
a) Considerar el potencial\(V(x) = -V_{0}\delta(x)\), que se esboza a continuación.
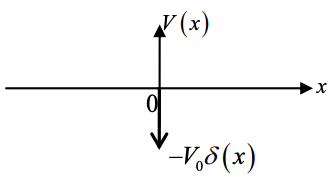
(i) Demostrar que la función de onda viene dada por\(\phi_{1}(x) = \sqrt{k}e^{-k|x|}\) donde\(k = \frac{mV_{0}}{\hbar^{2}}\)
(ii) Demostrar que la energía de los estados vinculados (E<0) es\(E_{1} = -\frac{mV_{0}^{2}}{2\hbar^{2}}\).
(b) Ahora agregue un segundo potencial de función delta en x = a.
es decir, si el hamiltoniano anterior era\(H_{1} = -\frac{\hbar^{2}}{2m} \frac{d^{2}}{dx^{2}}-V_{0}\delta(x)\), el nuevo hamiltoniano es\(H = H_{1}+V\) donde\(V = -V_{0}\delta(x-a)\)
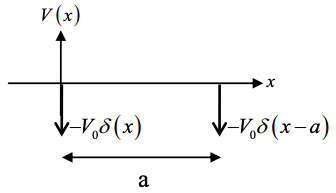
Que la función de onda del nuevo sistema sea aproximada por\(\psi=c_{1}\phi_{1}+c_{2}\phi_{2}\) donde\(\phi_{2} = \phi_{1}(x-a)\) y\(c_{1}\) y\(c_{2}\) son constantes.
La energía del uno mismo es\(\alpha = \left< \phi_{1}|H_{1}|\phi_{1} \right>\)
La interacción de salto es\(\beta = \left< \phi_{2}|V|\phi_{1} \right>\)
Además, definir la integral de superposición\(S = \left< \phi_{1}|\phi_{2} \right>\), y\(\gamma = \left< \phi_{1}|V|\phi_{1} \right>\)
Evaluando las expresiones
\( \left< \phi_{1} |H| \psi \right> = E \left< \phi_{1}|\psi \right> \)
y
\( \left< \phi_{2} |H| \psi \right> = E \left< \phi_{2}|\psi \right> \)
demuestre que
\ (\ left (\ begin {array} {cc}
\ alpha+\ gamma &\ alpha S+\ beta\
\ alpha S+\ beta &\ alpha+\ gamma
\ end {array}\ right)\ left (\ begin {array} {l}
c_ {1}\
c_ {2}
\ end {array}\ right) =E\ left (\ begin {array} {cc}
1 & S \\
S & 1
\ end {array}\ right)\ left (\ begin {array} {l}
c_ {1}\\
c_ {2}
\ end {array}\ right)\)
Ahora demuéstralo\(\alpha = \frac{-mV_{0}^{2}}{2\hbar},\ \beta = \frac{-mV_{0}^{2}}{\hbar^{2}}e^{-ka},\ S(1+ka)e^{-ka}, \text{ and } \gamma=\frac{-mV_{0}^{2}}{\hbar^{2}}e^{-2ka}\)
Dejar caer términos que contienen\(e^{-2ka}\), muestran que la matriz se reduce a\(E \approx \alpha \pm \beta\)
3. Para las moléculas donde cada átomo de carbono aporta al menos un electrón deslocalizado a un\(\pi\) orbital, podemos usar la aproximación de teoría orbital de electrones libres perimetrales, que se describe a continuación.
Supongamos que la molécula en cuestión es un anillo circular de átomos y asumir un potencial infinito de pozo cuadrado.
(a) Demostrar que los niveles de energía de una molécula bajo esta aproximación son
\( E = \frac{h^{2}m_{l}^{2}}{2m_{e}L^{2}} \)
donde\(m_{l}\) es un número entero, y L es el perímetro de la molécula.
Pista: El hamiltoniano en coordenadas polares viene dado por:
\( \hat{H} = \frac{\hbar^{2}}{2m_{e}}\left( \frac{d^{2}}{dr^{2}}+\frac{1}{r}\frac{d}{dr}+\frac{1}{r^{2}}\frac{d^{2}}{d\phi^{2}} \right) \)
(b) De acuerdo con la aproximación de la teoría orbital de electrones libres perimetrales, la estructura del nivel de energía del antraceno se muestra en la Figura 6.24.3, a continuación.
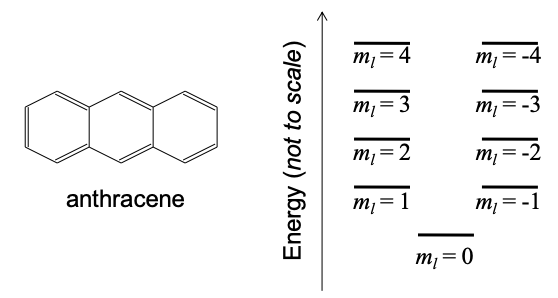
(i) ¿Por qué hay una solución para\(m_{l} = 0\) en el antraceno pero ninguna solución para n = 0 en el pozo cuántico infinito?
(ii) ¿Por qué hay soluciones para negativo\(m_{l}\) en antraceno pero no soluciones para n negativo en el pozo cuántico infinito? Pista: considerar el principio de exclusión de Pauli.
(c) Calcular los orbitales moleculares y la brecha HOMO-LUMO del antraceno. Tome a = 1.38Å como la longitud del enlace C-C. Supongamos que cada átomo de C dona 1 electrón a los orbitales fronterizos.
4. Considere la molécula periódica que consiste en dos tipos diferentes de átomos alternos que se ilustran a continuación (se muestran los orbitales fronterizos).

(a) ¿Cuántos átomos hay en la célula unitaria en esta molécula? Usando condiciones de límite periódicas y asumiendo funciones de onda molecular de la forma Bloch, encuentra los niveles de energía.
b) Encontrar la densidad de los estados.
5. La estructura de bandas de los cristales moleculares
Que\(\phi({\bf{r}})\) sea el HOMO de una molécula típica. Al igual que en la mayoría de las moléculas estables,\(\phi({\bf{r}})\) está completamente ocupada y contiene dos electrones.
A diferencia de los semiconductores cristalinos convencionales como el Si, las celdas unitarias en un cristal molecular se mantienen unidas por fuerzas débiles de van der Waals. Un valor típico para la interacción entre vecinos más cercanos en un sólido enlazado de van der Waals es
\( \beta=\left< \phi({\bf{r+R}})|H| \phi({\bf{r}})\right> \approx -10\ meV \)
donde H es el hamiltoniano para la interacción entre vecinos más cercanos y R es el conjunto de vectores de celosía que conectan la molécula en r con sus vecinos más cercanos.
a) Calcular la estructura de bandas de “valencia” de un cristal molecular cúbico de esta molécula. Vamos\(\left<\phi({\bf{r}})|H| \phi({\bf{r}})\right> = \alpha\). (Véase la Figura 6.24.5 a continuación).
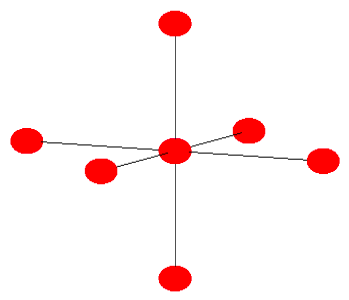
(b) Demostrar que todos los cristales moleculares con HOMO rellenos son aislantes.
6. Considere el siguiente polímero:

Supongamos que el espaciamiento entre átomos en la cadena principal lineal es\(a_{0}\), como se muestra. Además, supongamos que todos los átomos son el mismo elemento,\(\beta_{1}\) y\(\beta_{2}\) son las interacciones de salto entre los átomos como se muestra, la autoenergía en cada átomo es\(\alpha\), y asumir que cada átomo aporta un electrón.
(a) ¿Qué es la celda unitaria primitiva y el vector de celosía primitiva?
b) Demostrar que la relación de dispersión viene dada por
\( E = \alpha +\beta_{2}\ cos(ka_{0}) \pm \sqrt{\beta_{2}^{2}\ cos^{2}(ka_{0})+2\beta_{1}^{2}(1+cos(ka_{0}))} \)
c) ¿El polímero es metálico o aislante?
7. Transistores de grafeno y nanotubos de carbono
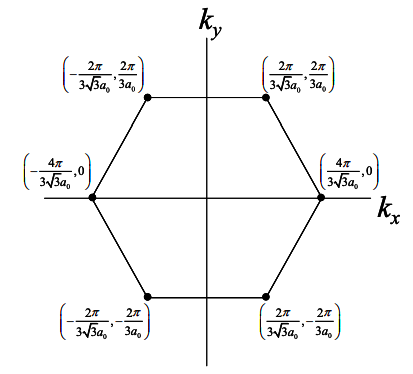
(a) Con referencia a la estructura de bandas del grafeno que se muestra a continuación, explique por qué el grafeno cuando se enrolla en nanotubos puede ser metálico o semiconductor?
(b) Utilizando la gráfica k -espacio que se muestra a continuación, determinar si los siguientes nanotubos (n, m) son metálicos o semiconductores. Recordemos que los nanotubos son láminas de grafeno enrolladas con vector de envoltura\(\bar{w}=na_{1}+ ma_{2}=(n,m)\).
i) (0,6)
ii) (N, N)
iii) (3,9)
iv) (3,5)
(c) En la actualidad, existe mucho interés en utilizar grafeno (a diferencia de nanotubos de carbono) como material de canal para transistores de efecto de campo. La idea es fabricar virutas enteras en una sola lámina de grafeno.
Primero el grafeno se deposita de alguna manera (este es un reto tecnológico en la actualidad). A continuación, se corta el grafeno. Finalmente, se depositan contactos y aisladores de puerta.
¿Por qué se corta el grafeno? Explicar con referencia a los modelos de partículas en una caja de conductores.
8. Nanotubos de Carbono
a) Demostrar las identidades en la Ecuación (6.21.3) y la Ecuación (6.21.4).
(b) Derivar la Ecuación (6.21.6) de la Ecuación (6.21.5).
9. Esta pregunta se relaciona con la molécula que se muestra a continuación.
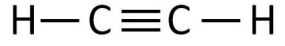
a) Escribir la matriz hamiltoniana para esta molécula en términos de los parámetros de unión apretada\(\alpha\), y\(\beta\).
b) Escribir la energía para este orbital molecular en términos de\(\alpha\) y\(\beta\).
c) Comparar la densidad de estados del HOMO y LUMO de la molécula anterior con la siguiente.