8.2: Apéndice 1 - Propagación de Paquete de Ondas de Electrones

Estados estacionarios y funciones propias

Hasta ahora, no hemos considerado la velocidad de los electrones porque no hemos considerado la dependencia temporal de las soluciones a la ecuación de Schrödinger. En la Parte 1, dividimos la Ecuación completa de Schrödinger en dos ecuaciones acopladas: una ecuación en el tiempo y otra en el espacio. La separación es posible cuando la energía potencial es constante en el tiempo. Entonces se pueden separar las dependencias espaciales y temporales de la solución, i.e.

\[ \Psi(x,t)=\psi(x)\zeta(t) \label{8.2.1} \]

La dependencia del tiempo es descrita por:

\[ E\zeta(t)=i \hbar \frac{d}{dt}\zeta(t) \label{8.2.2} \]

y la dependencia espacial viene dada por

\[ E\psi(x)= -\frac{\hbar^{2}}{2m}\frac{d^{2}}{dx^{2}}\psi(x)+V(x)\psi(x) \label{8.2.3}. \]

Las soluciones a estas ecuaciones acopladas se caracterizan por una densidad de probabilidad independiente del tiempo. La solución general a la Ecuación\ ref {8.2.2} es

\[ \zeta(t) = \zeta(0)\exp\left[ -i\frac{E}{\hbar}t \right] \label{8.2.4} \]

y la densidad de probabilidad es:

\[ |\Psi(x,t)|^{2} = |\psi(x)\zeta(t)|^{2}=|\psi(x)|^{2}|\zeta(0)|^{2} \label{8.2.5} \]

Debido a que la solución no evoluciona con el tiempo, se dice que es “estacionaria”. Estas soluciones son importantes y se conocen como “funciones propias”. Las funciones propias son extremadamente importantes en la mecánica cuántica. Se puede pensar en ellos como las funciones naturales de un sistema en particular. Cada función propia está asociada a una constante, conocida como el valor propio: en este caso la energía constante, E.

Una función de onda arbitraria, sin embargo, no necesariamente será una función propia o estacionaria. Por ejemplo, considere una función de onda construida a partir de dos funciones propias:

\[ | \psi(x)\rangle = a_{1}|\psi_{1}(x)\rangle + a_{2}|\psi_{2}(x)\rangle \label{8.2.6} \]

donde a y b son constantes. Esto se conoce como una combinación lineal de funciones propias. La solución completa es

\[ \Psi(x,t) = a_{1}\psi_{1}(x)e^{-i\frac{E_{1}}{\hbar}t} + a_{2}\psi_{2}(x)e^{-i\frac{E_{2}}{\hbar}t} \label{8.2.7} \]

Sustituir en la ecuación de Schrödinger da

\[ H|a_{1}\psi_{1}(x)e^{-i\frac{E_{1}}{\hbar}t} + a_{2}\psi_{2}(x)e^{-i\frac{E_{2}}{\hbar}t}\big\rangle =a_{1}E_{1}|\psi_{1}(x)e^{-i\frac{E_{1}}{\hbar}t}\big\rangle + a_{2}E_{2}|\psi_{2}(x)e^{-i\frac{E_{2}}{\hbar}t}\big\rangle \label{8.2.8} \]

es decir, la combinación lineal no es necesariamente en sí misma una función propia. No es estacionario: la fase de cada componente de función propia evoluciona a un ritmo diferente. La densidad de probabilidad muestra la interferencia dependiente del tiempo entre cada término de fase giratoria. Por ejemplo, suponiendo que\(a_{1}\),\(a_{2}\),\(\psi_{1}\) y\(\psi_{2}\) son reales:

\[ |\Psi{x,t}|^{2} = a_{1}^{2}\psi_{1}^{2}(x)+a_{2}^{2}\psi_{2}^{2}(x)+2a_{1}\psi_{1}(x)\psi_{2}(x) cos\left(\left( E_{2}-E_{1} \right) \frac{t}{\hbar}\right) \label{8.2.9}. \]

Completitud

No vamos a probar integridad en la clase. En cambio, simplemente declaramos que la propiedad de integridad de las funciones propias nos permite expresar cualquier función de buen comportamiento en términos de una combinación lineal de funciones propias. Es decir, si\(|\phi_{n}\rangle\) es una función propia, entonces se puede escribir una función de onda arbitraria de buen comportamiento

\[ |\psi\rangle = \sum_{n}a_{n}|\phi_{n}\big\rangle \label{8.2.10} \]

La integridad también requiere que el potencial sea finito dentro de la región de interés. Por ejemplo, ninguna combinación de funciones propias del pozo cuadrado infinito puede describir una amplitud de onda distinta de cero en las paredes.

Reexpresar la función de onda en términos de una suma ponderada de funciones propias es un poco como hacer una transformada de Fourier, excepto que en lugar de reexpresar la función de onda en términos de una combinación lineal de factores exp [i kx], estamos usando las funciones propias. \(^{†}\)

El problema ahora es la determinación de las constantes de ponderación,\(a_{n}\).

Para ello necesitamos la siguiente propiedad de eigenfunctions:

Ortogonalidad

Las funciones propias con diferentes valores propios son ortogonales. es decir, el corchete de las funciones propias correspondientes a diferentes valores propios es cero:

\[ \left< \phi_{j}|\phi_{i}\right> = 0,\ for\ i \neq j, \ E_{i}\neq E_{j} \label{8.2.11} \]

Si diferentes funciones propias tienen valores propios idénticos (es decir, la misma energía) se conocen como degenerados.

Cálculo de coeficientes

Partiendo de la ecuación\ ref {8.2.10} tenemos

\[ |\psi \rangle = \sum_{n}a_{n}|\phi_{n}\big\rangle \label{8.2.12} \]

Ahora, tomemos el corchete con una función propia\(\big\langle\phi_{k}|\)

\[ \left< \phi_{k}|\psi \right> =\left< \phi_{k} |\sum_{n}a_{n}|\phi_{n} \right> = \sum_{n}a_{n}\left< \phi_{k}|\phi_{n} \right> \label{8.2.13} \]

De la declaración de ortogonalidad en la Ecuación\ ref {8.2.11} tenemos

\[ \left< \phi_{k}|\phi_{n} \right> = \delta_{nk} \label{8.2.14} \]

donde\(\delta_{nk}\) está la función delta de Kronecker, es decir,\(\delta_{nk}=1\) solo cuando n = k.

Por lo tanto,

\[ a_{k}=\left< \phi_{k}|\psi \right> \label{8.2.15}. \]

Estos coeficientes son muy importantes.

Dado que las funciones propias son generalmente conocidas, a menudo el conjunto de coeficientes proporciona la información interesante en un problema particular. Esto puede quedar claro a partir de un ejemplo.

Un ejemplo: el pozo cuadrado en expansión

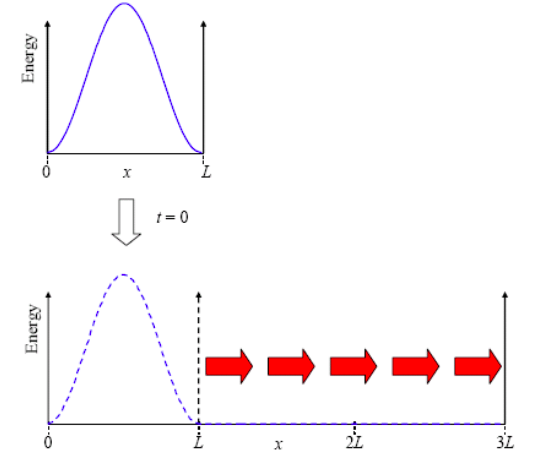
Considera un electrón que ocupa el estado fundamental de un pozo cuadrado infinito de longitud L. Como se muestra en la Figura\(\PageIndex{1}\), en el tiempo t = 0, el pozo de repente se triplica en tamaño. ¿Qué pasa con el electrón?

Figura\(\PageIndex{1}\): Un electrón se encuentra en el estado fundamental de un pozo de potencial infinito. De pronto el pozo infinito se expande instantáneamente a tres veces su tamaño anterior.

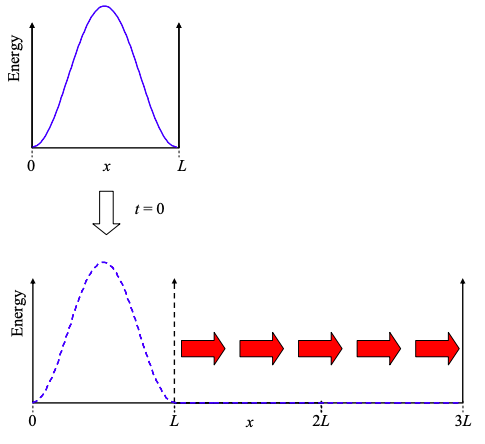
Comencemos a responder a esta pregunta considerando la función de onda previa a la expansión del pozo:\(^{†}\)

\[ \psi(x)=\sqrt{\frac{2}{L}}\sin(\pi x/L),\ 0\leq x\leq L \label{8.2.16} \]

Si sustituimos esto de nuevo en la Ecuación de Schrödinger podemos confirmar fácilmente que el efecto de operar sobre esta función de onda con el hamiltoniano es lo mismo que multiplicar la función de onda por una constante. i.e.

\[ H \bigg|\sqrt{\frac{2}{L}}\sin(\pi x/L) \bigg \rangle = E\bigg|\sqrt{\frac{2}{L}}\sin(\pi x/L) \bigg \rangle \label{8.2.17} \]

Así, esta función de onda es una función propia del pozo cuadrado original, y la constante, E, la energía, es el valor propio correspondiente a la función propia.

Ahora, la Ecuación\ ref {8.2.16} es la función propia de energía más baja para el potencial de pozo cuadrado infinito independiente del tiempo. La función de onda evoluciona en el tiempo según

\[ E\zeta(t)=i\hbar \frac{d}{dt}\zeta(t) \label{8.2.18} \]

Resolviendo la ecuación\ ref {8.2.2} da:

\[ \Psi(x,t) = \psi(x)\zeta(t) = \sqrt{\frac{2}{L}} \sin(\pi x/L)\exp\left[-i \frac{E}{\hbar}t\right] \label{8.2.19} \]

donde

\[ E =E_{L} = \frac{\hbar^{2}\pi^{2}}{2mL^{2}} \label{8.2.20} \]

La densidad de probabilidad, sin embargo, es independiente del tiempo:

\[ |\Psi(x,t)|^{2} =\frac{2}{L}\sin^{2}(\pi x/L),\ 0 \leq x \leq L \label{8.2.21} \]

Hemos verificado que la función propia es estacionaria, como debe ser.

Ahora, cuando el pozo se expande, la función de onda no puede cambiar instantáneamente. Para confirmar esto, considere un cambio escalonado en la función de onda en la Ecuación\ ref {8.2.2} — la energía tendería a hacerlo\(\infty\).

Pero los estados estacionarios del nuevo pozo son

\[ \psi(x) = \sqrt{\frac{2}{3L}}\sin(n\pi x /3L), \ \ 0\leq x\leq 3L \label{8.2.22} \]

es decir, la función de onda del electrón a t = 0 no es un estado estacionario en el pozo expandido. Para determinar la evolución de la función de onda electrónica en el tiempo, debemos reexpresar la función de onda en términos de las funciones propias del pozo expandido. Luego podemos calcular la evolución de cada función propia a partir de la Ecuación\ ref {8.2.2}.

La función de onda se describe ahora como una combinación lineal de funciones propias:

\ [\ psi (x) =\ sqrt {\ frac {2} {L}}\ sin (n\ pi x /L),\\ 0\ leq x\ leq L\\
=\ suma_ {n} a_ {n}\ sqrt {\ frac {2} {3L}}\ sin (n\ pi x /3L),\\ 0\ leq x\ q 3L\ etiqueta {8.2.23}\]

donde\(a_{n}\) es un conjunto de constantes, que ponderan las contribuciones de cada función propia.

Expresamos la función de onda como una combinación lineal de las funciones propias del pozo expandido. De la ecuación\ ref {8.2.15} tenemos

\[ \psi(x) = \sum_{n} a_{n} \sqrt{\frac{2}{3L}}\sin(n\pi x /3L), \ \ 0\leq x\leq 3L \label{8.2.24} \]

Así, los coeficientes son

\[ a_{n} = \left< \phi_{n}|\psi \right> = \int^{L}_{0} \sqrt{\frac{2}{3}} \sin(\pi x/L) \sqrt{\frac{2}{3L}} \sin(n \pi x/3L)dx \label{8.2.25} \]

Resolver da

\ [a_ {n} =
\ comenzar {casos}
\ frac {1} {\ sqrt {3}}\\\\\\\\\\\\\\\\\\\\\ n=3\
-\ frac {6\ sqrt {3}} {\ pi}\ frac {\ sin (n\ pi/3)} {n^ {2} -9}\\\ n\ neq 3
\ fin {casos}\ etiqueta {8.2.26}\]

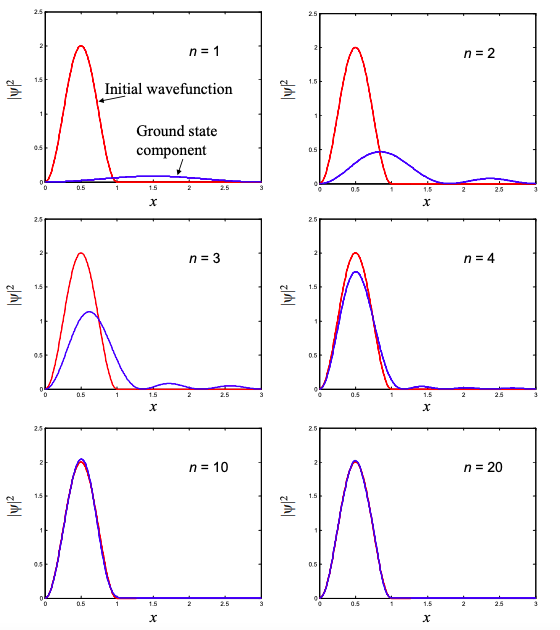
En la Figura\(\PageIndex{2}\) se grafica el efecto acumulativo de sumar las funciones propias ponderadas. Después de aproximadamente 10 funciones propias, la combinación lineal es una aproximación cercana a la función de onda inicial.

Figura\(\PageIndex{2}\): Aquí mostramos varias aproximaciones para la función de onda inicial. Necesitamos alrededor de 10 funciones propias ponderadas para una coincidencia cercana. El acuerdo mejora con funciones propias de adición.

A continuación, calculamos la evolución de la función de onda. De la ecuación\ ref {8.2.24}, obtenemos

\[ \Psi(x,t) = \sum_{n} a_{n} \sqrt{\frac{2}{3L}}\sin(n \pi x/3L) \exp\left[-i \frac{E_{n}}{\hbar}t \right], \ \ \ 0 \leq x \leq 3L \label{8.2.27} \]

donde

\[ E_{n} = \frac{n^{2} \pi^{2} \hbar^{2}}{2m(3L)^{2}} \label{8.2.28} \]

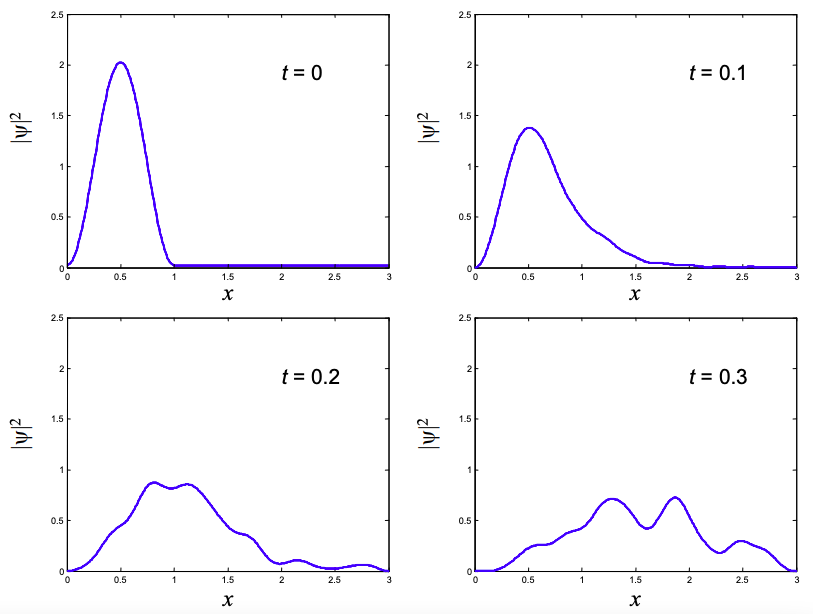
La evolución de la función de onda con el tiempo se muestra en la Figura\(\PageIndex{3}\), a continuación.

Figura\(\PageIndex{3}\): La evolución de la función ondulada después de la expansión de las paredes a t = 0.

Propagación de un paquete de ondas gaussianas

A continuación examinaremos la propagación de un conjunto de ondas gaussianas en el espacio libre. Nuevamente, ampliaremos la función de onda en términos de sus funciones propias.

Considera un electrón en el espacio libre. Que el paquete de ondas inicial sea un gaussiano.

\[ \psi(x,0) = (\pi L^{2})^{-1/4} \exp \left[ ik_{0}x \right] \label{8.2.29} \]

Tenga en cuenta que hemos introducido un factor de fase\(\exp \left[ ik_{0}x \right]\). Recordemos que multiplicar la función de onda espacial real por el factor de fase\(\exp \left[ ik_{0}x \right]\), es equivalente a desplazar la función de onda del espacio k por\(k_{0}\). Dado que la transformada de Fourier se centró en k = 0 antes del cambio, el factor de fase desplaza el valor de expectativa de k a\(k_{0}\). De ahí que el factor\(\exp \left[ ik_{0}x \right]\) da que el wavepacket tenga un impulso promedio distinto de cero.

Ahora, las funciones propias de la Ecuación de Schrödinger en el espacio libre son los exponenciales complejos

\[ \phi(k)= \exp[ikx] \label{8.2.30} \]

donde k es continuo.

Cada función propia evoluciona con el tiempo como

\[ \phi(k,t)= \exp[ikx]\exp\left[ -i\frac{E}{\hbar}t \right] \label{8.2.31} \]

Ampliando la función de onda como una combinación lineal de estas funciones propias que tenemos

\[ \psi(x,t)=\frac{1}{2\pi}\int^{+\infty}_{-\infty} A(k) \phi(k,t)dk \label{8.2.32} \]

\[ \psi(x,t)=\frac{1}{2\pi}\int^{+\infty}_{-\infty} A(k)\exp[ikx]\exp\left[ -i \frac{E}{\hbar} t\right]dk \label{8.2.33} \]

donde\(A(k)/2\pi\) describe la ponderación de cada función propia exponencial compleja.

Dado que\(\phi(k) = \exp[ikx]\), la ecuación\ ref {8.2.32} evaluada a t = 0 es simplemente la transformada inversa de Fourier:

\[ \psi(x) = \frac{1}{2\pi} \int^{+\infty}_{-\infty} A(k)\exp[ikx] dk \label{8.2.34} \]

Así, A (k) se determina a partir de la transformada de Fourier de la función de onda

\[ A(k) = \left< \phi(k)|\psi(x,0) \right> = \int^{+\infty}_{-\infty} \psi(x,0)e^{-ikx}dx = (4\pi L^{2})^{1/4}\exp \left[ -\frac{L^{2}(k-k_{0})^{2}}{2} \right] \label{8.2.35} \]

Ahora, antes de que podamos sustituir A (k) de nuevo en la Ecuación\ ref {8.2.32} para obtener la evolución temporal de\(\psi(x,t)\) necesitamos considerar la posible k dependencia de la energía, E.

En general la relación entre E y k se conoce como la relación de dispersión.

La relación de dispersión es importante porque la propagación de un electrón en el espacio libre, o en un material particular está determinada por la relación de dispersión. Consideremos algunos ejemplos.

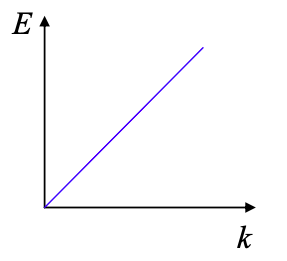
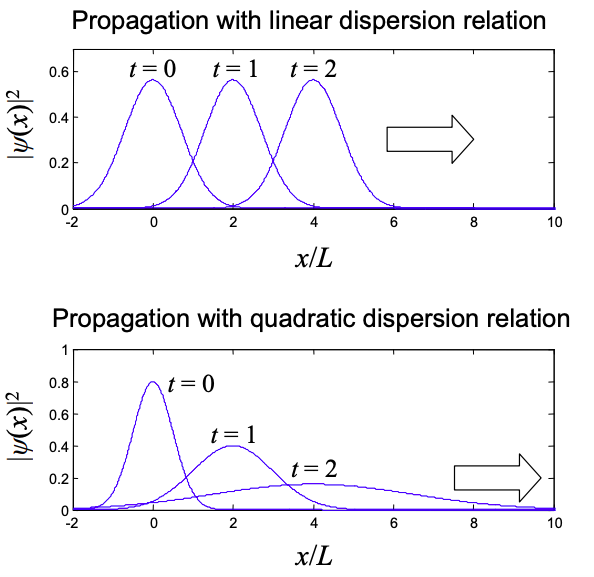
Relación de dispersión lineal

La relación de dispersión determina cómo se propaga el conjunto de ondas en el tiempo. Por ejemplo, si en lugar de un electrón estábamos considerando un fotón con\(E = \hbar\omega = \hbar c k\), la relación de dispersión es lineal y el fotón no se propaga a medida que se propaga.

Figura\(\PageIndex{4}\): Una relación de dispersión lineal.

El factor dependiente del tiempo es

\[ \exp\left[ -i \frac{E}{\hbar}t \right] \equiv \exp[-i\omega t] = \exp \left[ -ickt \right] \label{8.2.36}. \]

Resolviendo Ecuación\ ref {8.2.32} da

\[ \psi(x,t) = \frac{1}{(\pi L^{2})^{1/2}}\exp\left[ -\frac{(x-ct)^{2}}{L^{2}} \right] \label{8.2.37} \]

Así, la densidad de probabilidad es simplemente la función original desplazada linealmente en el tiempo:

\[ |\psi(x,t)|^{2} = \frac{1}{(\pi L^{2})^{1/2}}\exp\left[ -\frac{(x-ct)^{2}}{L^{2}} \right] \label{8.2.38} \]

Relación de dispersión cuadrática

Para las funciones propias de onda plana, sin embargo, la relación de dispersión es cuadrática y tenemos

\[ E = \frac{\hbar^{2}k^{2}}{2m} \label{8.2.39} \]

Figura\(\PageIndex{5}\): Una relación de dispersión cuadrática.

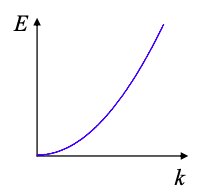
Como hemos visto, las partículas en una caja también tienen relaciones de dispersión cuadráticas.

Así, el factor dependiente del tiempo es

\[ \exp \left[ -i\frac{E}{\hbar} t\right] \equiv \exp[-i\omega t] \exp\left[ -i \frac{\hbar k^{2}}{2m}t \right] \label{8.2.40} \]

Resolviendo Ecuación\ ref {8.2.32} da

\[ \psi(x,t) = \frac{1}{(\pi L^{2})^{1/4}} \frac{1}{\sqrt{1+i\hbar t/mL^{2}}} \exp\left[ i\left(k_{0}x-\frac{\hbar k_{0}^{2}t}{2m} \right) \right]\exp\left[- \frac{(x-\hbar k_{0}t/m)^{2}}{2L^{2}(1+i\hbar t/mL^{2})} \right] \label{8.2.41} \]

y

\[ |\psi(x,t)|^{2}=\left(2\pi [\Delta x(t)]^{2} \right)^{-1/2} \exp \left[ -\frac{(x-\hbar k_{0}t/m)^{2}}{2[Delta x(t)]^{2}} \right] \label{8.2.42} \]

donde

\[ [\Delta x(t)]^{2}=\frac{L^{2}}{2}\left( 1+\left( \frac{\hbar t}{mL^{2}}\right)^{2} \right) \label{8.2.43} \]

Figura\(\PageIndex{6}\): Evolución de un conjunto de ondas gaussianas para las relaciones de dispersión lineal y cuadrática.

Velocidad de Grupo

Al igual que con una onda clásica, la velocidad promedio del conjunto de ondas es la velocidad de grupo, definida como la derivada de tiempo del valor de expectativa de posición:

\[ v_{g}=\frac{d}{dt}\langle x \rangle = \left< \frac{1}{\hbar} \frac{dE}{dk}\right> = \left< \frac{d\omega}{dk} \right> \label{8.2.44} \]

Si el conjunto de ondas tiene un alto pico en el espacio k, es posible simplificar la Ecuación\ ref {8.2.44} evaluando\(d\omega/dk\) al valor de expectativa de k:

\[ v_{g} = \left< \frac{d\omega}{dk} \right> \approx \frac{d\omega}{dk} \biggr \rvert_{\left< k\right>} \label{8.2.45} \]

Para la relación de dispersión lineal,\(d\omega/dk\) es constante por lo que no necesitamos la aproximación:

\[ v_{g} = \left< \frac{d\omega}{dk} \right> = \left< \frac{\hbar k}{m} \right> = \frac{\hbar k_{0}}{m} \label{8.2.46} \]

Dado que\(\hbar k_{0}\) es el valor esperado del impulso, esta es efectivamente la velocidad promedio.

Problemas

1. Considerar el electrón en el expandido bien discutido en las notas. Simular numéricamente la función de onda en función del tiempo. Usando la simulación o de otra manera, determinar el valor esperado de la energía antes y después de que el pozo se expanda? Predecir el comportamiento de los valores de expectativa de posición e impulso en función del tiempo.

Figura\(\PageIndex{7}\): El pozo en expansión.

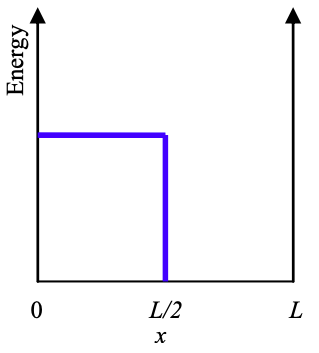
2. Considera la función de onda en un pozo cuadrado infinito de ancho L ilustrado a continuación en el tiempo t = 0. ¿Cómo evolucionará la función de onda para t > 0. ¿Volverá alguna vez la función de onda a su posición original? Si es así, ¿en qué momento t = T ocurrirá esto?

Figura\(\PageIndex{8}\): Un estado inicial dentro de un pozo cuántico.

3. Derivar la expresión para la propagación de un conjunto de ondas gaussianas con la relación de dispersión lineal\(E = \hbar \omega = \hbar ck\). (Ecuación\ ref {8.2.37})

\(^{†}\)Tenga en cuenta que exp [i kx] proporciona un conjunto continuo de funciones propias para estados no unidos, es decir, la expansión en términos de funciones propias es la transformada de Fourier.

\(^{†}\)Obsérvese que relativo al análisis de pozo cuadrado anterior (ver Figura 1.28.1) hemos desplazado el eje x aquí de tal manera que la pared izquierda está en x = 0.