3.4: Respuestas Transitorias Simples de Sistemas de Primer Orden, Constantes de Tiempo de Primer Orden y Tiempos de Ajuste

Última actualización
Guardar como PDF

Page ID: 84707

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El adjetivo transitorio se aplica a la respuesta del sistema que es dinámica durante un intervalo de tiempo finito (a menudo llamado el tiempo de asentamiento), pero es esencialmente estática a partir de entonces.

Consideremos el problema ^de primer orden presentado en el Capítulo 2,

\[\dot{x}-a x=b U e^{-w t}, x(0)=x_{0}, \text { solve for } x(t), t>0 \nonumber \]

con solución,

\[x(t)=x_{0} e^{a t}+\frac{b U}{a+w}\left(e^{a t}-e^{-w t}\right), \text { for } t \geq 0 \nonumber \]

Si dejamos\(w\) = 0, entonces el término de entrada se convierte en la función step,\(U\left[e^{-w t}\right]_{w=0}\) =\(U H(t)=U\) for\(t\) < 0,\(H(t)\) siendo la función de paso de unidad Heaviside definida en la Sección 2.4. Entonces el problema y la solución se convierten en:

\[\dot{x}-a x=b U, x(0)=x_{0}, \text { solve for } x(t), t>0 \nonumber \]

\[x(t)=\frac{b U}{(-a)}\left(1-e^{-(-a) t}\right)+x_{0} e^{-(-a) t}, \text { for } t \geq 0\label{eqn:3.3} \]

En Ecuación\(\ref{eqn:3.3}\), escribimos\(a=-(-a)\) porque usualmente\(a\) < 0 para sistemas de ingeniería, como en la Ecuación 3.3.3. Queremos considerar dos casos especiales de ecuación de solución\(\ref{eqn:3.3}\):

respuesta de condición inicial pura para\(U\) = 0 y
respuesta pura de paso para\(x_{0}\) = 0.

Respuesta estable a la condición inicial (IC)

\[x(t)=x_{0} e^{-(-a) t}, \text { for } t \geq 0\label{eqn:3.4} \]

Definir la ^1ª constante de tiempo del sistema de pedidos,

\[\tau_{1} \equiv \frac{1}{(-a)}\label{eqn:3.5} \]

Por ejemplo, la constante de tiempo para la rueda de reacción de la Ecuación 3.3.3 es\(\tau_{1} \equiv \frac{J}{c_{\theta}}\). Debe satisfacerse, utilizando la Tabla 3.1.1 si es necesario, que la cantidad\(J / c_{\theta}\) tiene la dimensión de tiempo (unidad de segundo). Con esta definición de constante de tiempo\(\tau_{1}\), la ecuación de solución\(\ref{eqn:3.4}\) se convierte en:

\[x(t)=x_{0} e^{-t / \tau_{1}} \equiv x_{0} \exp \left(-t / \tau_{1}\right), \text { for } t \geq 0\label{eqn:3.6} \]

Figura\(\PageIndex{1}\): Respuesta ^de condición inicial de primer orden

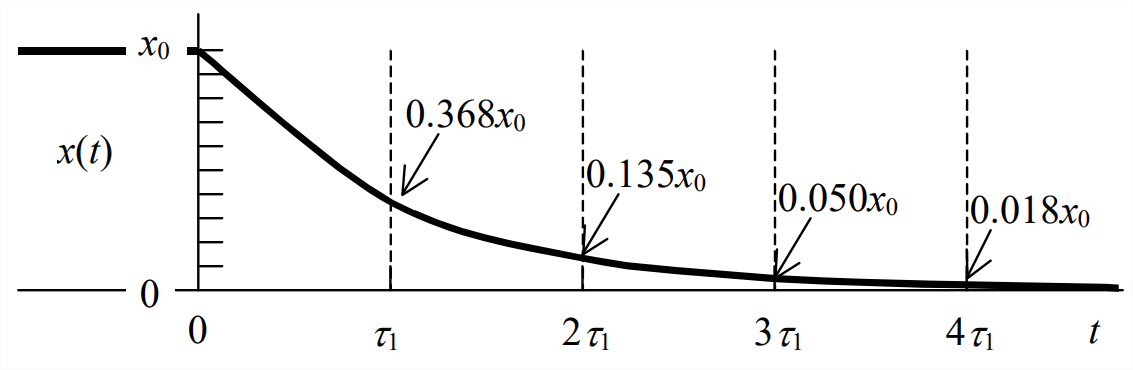
En la constante de tiempo\(t=\tau_{1}\),, la respuesta ha decaído a\(e^{-1}\) = 37% del valor inicial. El otro tiempo “hito” al que nos referiremos muchas veces es\(t=4 \tau_{1}\), al que llamamos el tiempo de asentamiento, momento en el que la respuesta ha decaído a\(e^{−4}\) = 2% del valor inicial. Para la mayoría de los propósitos prácticos de ingeniería, se considera que este tiempo de sedimentación es el tiempo requerido para que la respuesta alcance esencialmente su valor final de estado estacionario, que es\(x\) = 0 en este caso de respuesta IC. Matemáticamente,\(x\rightarrow 0\) sólo como\(t \rightarrow \infty\).

Si la constante\(a\) es positiva, entonces escribimos solución IC Ecuación\(\ref{eqn:3.4}\) como\(x(t)=x_{0} e^{a t}\). La respuesta matemática representada por esta solución es ilimitada:\(x \rightarrow \infty\) as\(t \rightarrow \infty\). En realidad, ninguna variable de ingeniería nunca se volverá infinita: a medida que la variable se vuelve grande, algo en el sistema fallará o se sobrecargará, o el sistema se volverá no lineal, o la respuesta será limitada por un gobernador, etc. A pesar de que la respuesta real no será infinita, una respuesta matemática lineal exponencialmente creciente como esta suele ser indeseable para fines prácticos; un sistema de ingeniería que exhibe este tipo de respuesta se considera un sistema de ingeniería con inestabilidad. Por otro lado, una constante negativa\(a\) es estable.

La constante de tiempo\(\tau_1\) es una cantidad tan importante para los sistemas estables ^de primer orden que volveremos a fundir el sistema estándar de ^primer orden ODE en términos de\(\tau_1\), en lugar de constante\(a\), usando Ecuación\(\ref{eqn:3.5}\). Así, en lugar de analizar la Ecuación 1.2.1\(\dot{x}-a x=b u(t)\), en lo sucesivo usualmente consideraremos la siguiente forma estable estándar para los sistemas ^de primer orden:

\[\dot{x}+\frac{1}{\tau_{1}} x=b u(t)\label{eqn:3.7} \]

Respuesta escalonada estable

En Ecuación\(\ref{eqn:3.3}\), establecemos\(x_0\) = 0 y usamos la ecuación de definición de constante de tiempo\(\ref{eqn:3.5}\) para obtener

\[x(t)=b U \tau_{1}\left(1-e^{-t / \tau_{1}}\right) \equiv b U \tau_{1}\left[1-\exp \left(-t / \tau_{1}\right)\right], \text { for } t \geq 0\label{eqn:3.8} \]

La figura\(\PageIndex{2}\) es una gráfica de la subida exponencial a un valor final positivo que se indica en la Ecuación\(\ref{eqn:3.8}\).

^{Figura\(\PageIndex{2}\): Respuesta de primer paso de orden}

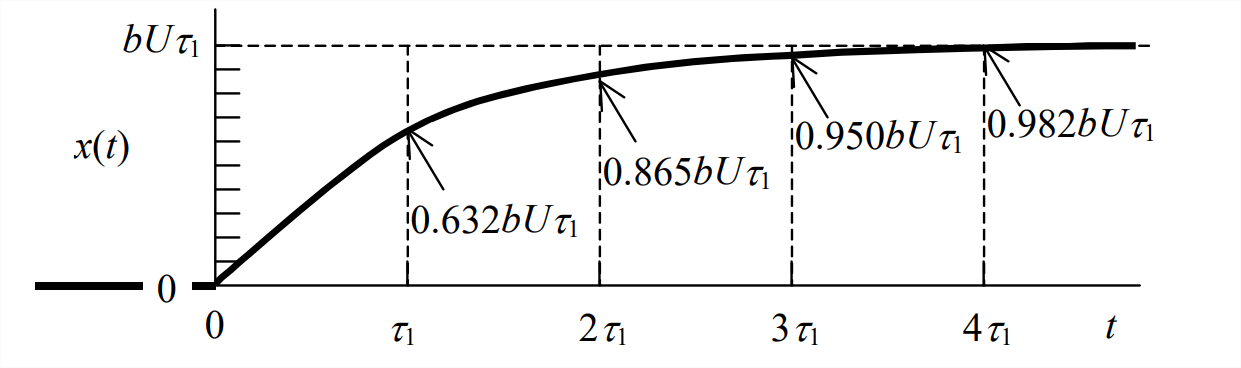
El valor final de la respuesta unidad-paso es\(b U \tau_{1}\), y se aborda asintóticamente como\(t \rightarrow \infty\). En la constante de tiempo\(t=\tau_{1}\),, la respuesta ha subido del IC de cero a\(1-e^{-1}\) = 63%. En\(t=4 \tau_{1}\), el tiempo de asentamiento, la respuesta ha subido a\(1-e^{-4}\) = 98% del valor final.

Las soluciones de respuesta escalonada como Ecuación\(\ref{eqn:3.8}\) suelen ser una aproximación a la respuesta real ya que, en realidad, rara vez se puede lograr un cambio de paso puro y discontinuo en una cantidad de entrada física. Sin embargo, la entrada de pasos es una aproximación suficientemente cercana a muchas entradas físicas reales que las soluciones de respuesta escalonada como la ecuación\(\ref{eqn:3.8}\) son aproximaciones cercanas a las respuestas físicas reales.

Consideremos nuevamente la rueda de reacción de la sección anterior. Denotemos una entrada de paso desde el motor como\(M_{m}(t)=M \times H(t)\). Entonces la ecuación ODE 3.3.3 se convierte en

\[\dot{p}-a p=b M_{m}(t)=b M H(t)=b M \text { for } t>0, \text { where } a=-\frac{c_{\theta}}{J}=-\frac{1}{\tau_{1}} \text { and } b=\frac{1}{J}\label{eqn:3.9} \]

Entonces la constante de tiempo es\(\tau_{1}=-1 / a=J / c_{\theta}\), y la ecuación de solución\(\ref{eqn:3.8}\) se convierte

\[p(t)=b M \tau_{1}\left(1-e^{-t / \tau_{1}}\right)=\frac{1}{J} M \frac{J}{c_{\theta}}\left(1-e^{-t / \tau_{1}}\right)=\frac{M}{c_{\theta}}\left(1-e^{-t / \tau_{1}}\right) \mathrm{rad} / \mathrm{sec}, \text { for } t \geq 0\label{eqn:3.10} \]

Tenga en cuenta que en este caso adaptamos la ecuación de solución matemática “estándar”\(\ref{eqn:3.8}\) a un problema físico particular. Este enfoque es común en la dinámica del sistema. En otras palabras, no siempre es necesario resolver una ODE para cada nuevo problema físico; si ya se ha derivado una solución ODE estándar, es posible que simplemente adapte esa solución estándar al problema físico en cuestión, en lugar de volver a derivar la solución ODE.