4.2: Respuesta de un sistema de primer orden a un coseno aplicado repentinamente

^{Primero, derivamos una solución completa de la manera convencional para el estándar original ODE de 1 er orden\(\dot{x}-a x=b u(t)\) [Ecuación 1.2.1], con IC\(x(0)=x_{0}\), y con la entrada coseno aplicada repentinamente (at\(t\) = 0)\(u(t)=U \cos \omega t\),\(t\) > 0, donde\(U\) es una amplitud constante [Problema} 2.12.2].

\[\mathrm{ODE}+\mathrm{IC}: \dot{x}-a x=b U \cos \omega t=b U \frac{e^{j \omega t}+e^{-j \omega t}}{2}, x(0)=x_{0}, \text { find } x(t) \text { for } t>0\label{eqn:4.1} \]

Transformación Laplace de ODE + IC:\(s X(s)-x_{0}-a X(s)=\frac{b U}{2}\left(\frac{1}{s-j \omega}+\frac{1}{s+j \omega}\right)\)

Resolver para\(X(s)\):

\[X(s)=\frac{x_{0}}{s-a}+\frac{b U}{2} \frac{1}{(s-a)}\left(\frac{1}{s-j \omega}+\frac{1}{s+j \omega}\right) \nonumber \]

Expansión de fracción parcial completada (Problema 2.8):

\[X(s)=\frac{x_{0}}{s-a}+\frac{b U}{2} \frac{1}{a^{2}+\omega^{2}}\left(\frac{2 a}{s-a}+\frac{-a-j \omega}{s-j \omega}+\frac{-a+j \omega}{s+j \omega}\right) \nonumber \]

Transformación inversa:

\[ \begin{align} x(t) &=x_{0} e^{a t}+\frac{b U}{a^{2}+\omega^{2}}\left[a e^{a t}+\frac{1}{2}\left((-a-j \omega) e^{j \omega t}+(-a+j \omega) e^{-j \omega t}\right)\right] \\[4pt] \quad x(t)&=x_{0} e^{a t}+\frac{b U}{a^{2}+\omega^{2}}\left[a e^{a t}+\frac{1}{2}\left((-a)\left(e^{j \omega t}+e^{-j \omega t}\right)+\omega \frac{e^{j \omega t}-e^{-j \omega t}}{j}\right)\right] \\[4pt] x(t)&=x_{0} e^{a t}+\frac{b U}{a^{2}+\omega^{2}}\left(a e^{a t}-a \cos \omega t+\omega \sin \omega t\right), t \geq 0 \\[4pt] x(t) &= x_{0} e^{a t}+\left(\frac{b}{-a}\right) \frac{U}{\left[1+\left(\frac{\omega}{-a}\right)^{2}\right]}\left[-e^{a t}+\cos \omega t+\left(\frac{\omega}{-a}\right) \sin \omega t\right], t \geq 0\label{eqn:4.2} \end{align} \]

^{A continuación, adaptamos la solución Ecuación\(\ref{eqn:4.2}\) del problema general de primer orden Ecuación\(\ref{eqn:4.1}\) al sistema amortiguador-resorte (puntal de choque ideal) de la Figura 3.7.1 con entrada de fuerza coseno aplicada repentinamente\(f_{x}(t)=F \cos \omega t\), para lo cual el problema comparable de ODE + IC es}

\[c \dot{x}+k x=F \cos \omega t, x(0)=x_{0}, \text { find position } x(t) \text { for } t>0\label{eqn:4.3} \]

Comparando Ecuación\(\ref{eqn:4.3}\) con Ecuación\(\ref{eqn:4.1}\), definimos\(U\)\(\equiv\)\(F\), luego las otras constantes de la ecuación estándar se convierten en

\[a=-\frac{k}{c} \equiv-\frac{1}{\tau_{1}} \Rightarrow \text { time constant } \tau_{1} \equiv \frac{1}{-a}=\frac{c}{k} \quad \text { and } \quad b=\frac{1}{c} \text { and } \frac{b}{-a}=\frac{1}{k} \nonumber \]

\[\Rightarrow \quad x(t)=x_{0} e^{-t / \tau_{1}}+\frac{F}{k}\left(\frac{1}{1+\left(\omega \tau_{1}\right)^{2}}\right)\left(-e^{-t / \tau_{1}}+\cos \omega t+\omega \tau_{1} \sin \omega t\right), t \geq 0\label{eqn:4.4} \]

Es instructivo estudiar la naturaleza física de la ecuación de respuesta\(\ref{eqn:4.4}\) en el contexto de un ejemplo numérico específico. Considerar un puntal de choque ideal con la condición inicial\(x_0\) = -2 m, y con los parámetros del sistema\(c=1 / \pi\) N/ (m/s) = 0.3183 N-S/m y\(k\) = 1 N/m, de manera que la constante de tiempo\(\tau_{1}=1 / \pi\) s = 0.3183 s. Deje que la magnitud de la fuerza coseno sea\(F\) = 1.5 N, y deje que el periodo de el coseno sea\(T_p\) = 1 s/ciclo. Por lo tanto, la frecuencia cíclica es\(f\) = 1 Hz (ciclo/s), y la frecuencia circular es\(\omega = 2\pi\) radianes/s. (Periodo, frecuencia y fase de las señales periódicas se discuten de manera más general en la Sección 4.4.) La solución numérica de Ecuación\(\ref{eqn:4.4}\) con estos parámetros para el tiempo 0\(\leq\)\(t\)\(\leq\) 3 s se calcula y grafica en las siguientes operaciones de MATLAB.

%MATLABdemo41.m

%Damper-spring ideal shock strut response to IC + cosine forcing

c=1/pi;k=1; %system viscous damping & stiffness constants, SI units

F=1.5;Tp=1; %cosine forcing: amplitude (N), period (sec)

xo=-2; %initial displacement (m)

w=2*pi/Tp; %circular frequency of cosine forcing (rad/sec)

t1=c/k;denom=1+(w*t1)^2;

t=0:0.01:3*Tp; %time instants for forced response

fx=F*cos(w*t);

x=(xo-(F/k)/denom)*exp(-t/t1)+(F/k)/denom*(cos(w*t)+w*t1*sin(w*t));

plot(t,fx,'k',t,x,'k.'),grid,xlabel('Time t (sec)'),... ylabel('Force input f_x(t) (N) and displacement output x(t) (m)'),... title('Time response of an ideal shock strut to IC + cosine input')

Hello world!

Script de archivo M de MATLAB:

%Matlabdemo41.m

% amortiguador-resorte respuesta de puntal de choque ideal al forzamiento de coseno IC +

c=1/pi; k=1; %constantes viscosas de amortiguación y rigidez del sistema, unidades SI

F=1.5; Tp=1; %forzamiento coseno: amplitud (N), periodo (seg)

xo=-2; %desplazamiento inicial (m)

W=2*pi/tp;% de frecuencia circular de forzamiento de coseno (rad/seg)

t1=c/k; denom=1+ (w*t1) ^2;

t= 0:0. 01:3 *Tp;% instantes de tiempo para respuesta forzada

FX=F*cos (w*t);

x = (xo- (f/K) /denom) *exp (-t/t1) + (f/K) /denom* (cos (w*t) +w*t1*sin (w*t));

parcela (t, fx, 'k', t, x, 'k.') , grid, xlabel ('Tiempo t (seg) '),... ylabel ('Entrada de fuerza f_x (t) (N) y salida de desplazamiento x (t) (m)'),... title ('Respuesta de tiempo de un puntal de choque ideal a IC + entrada de coseno')

Comando/respuestas de MATLAB:

>> MatlabDemo41

El gráfico de entrada\(f_x(t)\) y respuesta\(x(t)\) se encuentra a continuación (después de la edición de figuras en MATLAB, Versión 6 o posterior, para aplanar la relación de aspecto y distinguir las dos curvas).

Figura\(\PageIndex{1}\)

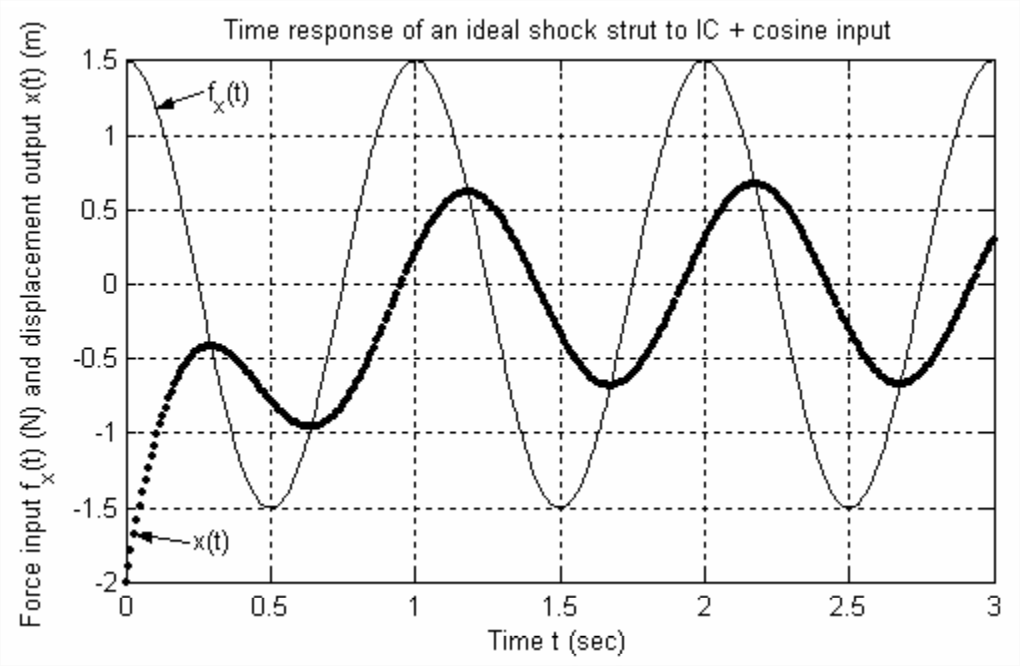
Observemos desde la gráfica algunas características importantes de la respuesta:

• Como se calculó anteriormente, la constante de tiempo de los términos de decaimiento exponencial en la Ecuación\(\ref{eqn:4.4}\) [los dos términos que implican\(\exp \left(-t / \tau_{1}\right)\)] es\(\tau_{1}\) = 0.3183 s, por lo que el tiempo de asentamiento para esos términos es\(4 \tau_{1}\) = 1.273 s. En otras palabras, los términos de decaimiento exponencial en esencialmente\(x(t)\) han desaparecido después de alrededor de 1.3 s de respuesta, y esto queda claro a partir de la gráfica. Debido a que los términos de decaimiento exponencial son relativamente efímeros, a menudo nos referimos a ellos como la parte “transitoria” de la solución total.
• Después de que los términos de decaimiento exponencial hayan desaparecido, solo\(\ref{eqn:4.4}\) quedan los\(\sin \omega t\) términos\(\cos \omega t\) y de Ecuación. De la gráfica se desprende que esos dos términos se combinan para hacer una sola sinusoide a frecuencia \(\omega\), y que la\(x(t)\) sinusoide de estado estacionario restante se desplaza en el tiempo por un retardo de tiempo constante desde la\(F_x(t)\) sinusoide. Esta respuesta sinusoidal en estado estacionario es lo que llamamos la respuesta de frecuencia, y derivaremos ecuaciones que la describen explícitamente en el resto del capítulo.