4.3: Respuesta de frecuencia del sistema amortiguador-resorte de primer orden

Para extraer la respuesta sinusoidal en estado estacionario de la ecuación\(x_{ss}(t)\) de respuesta total 4.2.7, dejamos caer los términos de decaimiento exponencial transitorio:

\[x_{s s}(t)=\frac{F}{k}\left(\frac{1}{1+\left(\omega \tau_{1}\right)^{2}}\right)\left(\cos \omega t+\omega \tau_{1} \sin \omega t\right)\label{eqn:4.5} \]

Podemos escribir Ecuación\(\ref{eqn:4.5}\) en una forma que sea más expresiva físicamente mediante el uso de alguna manipulación algebraica y la identidad trigonométrica general,

\[\cos \theta \times \cos \phi-\sin \theta \times \sin \phi=\cos (\theta+\phi)\label{eqn:4.6} \]

La manipulación algebraica involucra los términos sinusoidalmente variables de la Ecuación\(\ref{eqn:4.5}\). Por generalidad, supongamos que cada término se multiplica por un coeficiente general,\(C\) o bien\(-S\), para que esos términos puedan escribirse y manipularse como

\[C \cos \omega t-S \sin \omega t=\sqrt{C^{2}+S^{2}}\left(\cos \omega t \frac{C}{\sqrt{C^{2}+S^{2}}}-\sin \omega t \frac{S}{\sqrt{C^{2}+S^{2}}}\right) \nonumber \]

Ahora identificamos los coeficientes de\(\cos \omega t\) y entre\(\sin \omega t\) paréntesis como ellos mismos que representan funciones trigonométricas:\(\frac{C}{\sqrt{C^{2}+S^{2}}} \equiv \cos \phi\) y\(\frac{S}{\sqrt{C^{2}+S^{2}}} \equiv \sin \phi\), donde el ángulo\(\phi\) viene dado por una función tangente de cuatro cuadrantes,

\[\phi=\tan ^{-1}\left(\frac{S}{C}\right)\label{eqn:4.7} \]

Figura\(\PageIndex{1}\)

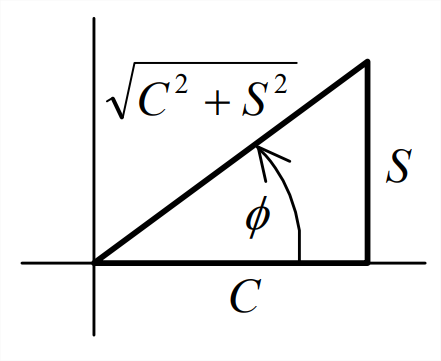
Estas relaciones trigonométricas se ilustran a la izquierda en el dibujo de un triángulo rectángulo.

Entonces, con la ecuación de identidad\(\ref{eqn:4.6}\), la suma trigonométrica se convierte en

\[C \cos \omega t-S \sin \omega t=\sqrt{C^{2}+S^{2}}(\cos \omega t \cos \phi-\sin \omega t \sin \phi)=\sqrt{C^{2}+S^{2}} \cos (\omega t+\phi)\label{eqn:4.8} \]

Asociando Ecuación\(\ref{eqn:4.5}\) con Ecuación\(\ref{eqn:4.8}\), tenemos\(C=1\),\(S=-\omega \tau_{1}\). Por tanto, la ecuación\(\ref{eqn:4.5}\) se convierte

\[x_{s s}(t)=\frac{F}{k}\left(\frac{1}{1+\left(\omega \tau_{1}\right)^{2}}\right) \sqrt{1+\left(\omega \tau_{1}\right)^{2}} \cos (\omega t+\phi) \nonumber \]

\[x_{s s}(t)=\frac{F}{k} \frac{1}{\sqrt{1+\left(\omega \tau_{1}\right)^{2}}} \cos (\omega t+\phi) \equiv X(\omega) \cos (\omega t+\phi(\omega)), \quad \phi(\omega)=\tan ^{-1}\left(\frac{-\omega \tau_{1}}{1}\right)\label{eqn:4.9} \]

Comparemos la respuesta de estado estacionario (salida),\(x_{s s}(t)\) de Ecuación\(\ref{eqn:4.9}\), con la excitación (entrada),\(f_{x}(t)=F \cos \omega t\). La magnitud de la respuesta, que es una función de la frecuencia de excitación\(\omega\), es

\[X(\omega)=\frac{F}{k} \frac{1}{\sqrt{1+\left(\omega \tau_{1}\right)^{2}}}\label{eqn:4.10} \]

A menudo nos ocuparemos de la relación de magnitud, definida como la magnitud de la respuesta dividida por la magnitud de la excitación,

\[\frac{X(\omega)}{F}=\frac{1}{k} \frac{1}{\sqrt{1+\left(\omega \tau_{1}\right)^{2}}}\label{eqn:4.11} \]

La fase (o ángulo de fase, ya que es un ángulo en radianes o grados) de respuesta relativa a la fase de la excitación también es función de la frecuencia de excitación \(\omega\):

\[\phi(\omega)=\tan ^{-1}\left(-\omega \tau_{1}\right)\label{eqn:4.12} \]

En general, si el ángulo de fase\(\phi\) es positivo, 0°\(\phi\) < < 180°, se denomina plomo de fase, porque los picos y ceros de la respuesta ocurren en el tiempo antes que los de la excitación. Si el ángulo de fase\(\phi\) es negativo, −180° ≤\(\phi\) < 0°, se denomina retardo de fase, porque los picos y ceros de la respuesta ocurren en el tiempo después de los de la excitación. Se dice que la respuesta está en fase si\(\phi\) = 0° exactamente, y fuera de fase si\(\phi\) = −180° exactamente. ^{Para el sistema estable estándar de primer orden considerado actualmente\(\phi(\omega)=\tan ^{-1}\left(-\omega \tau_{1}\right)\), que es un retraso de fase, siempre negativo en el cuadrante 4, −90° <\(\phi\) < 0°, con\(\phi\rightarrow\) 0° para muy pequeños\(\omega\) y\(\phi\rightarrow\) -90° para muy grandes\(\omega\).}

Se considera que la función frecuencia-respuesta (FRF abreviada) consiste tanto en la relación de magnitud, Ecuación\(\ref{eqn:4.11}\) en este caso, como en el ángulo de fase, Ecuación\(\ref{eqn:4.12}\) en este caso. Veremos más adelante que ambas funciones se pueden expresar juntas en una ecuación matemática como una única función compleja de frecuencia. Es común en la práctica de ingeniería trazar estas dos funciones reales de frecuencia\(\omega\) en un par de gráficas sobre-y-debajo en el formato de Figura\(\PageIndex{2}\), que representa Ecuaciones\(\ref{eqn:4.11}\) y\(\ref{eqn:4.12}\) específicamente. Este formato es un tipo de diagrama Bode (después de Hendrik Wade Bode, matemático estadounidense, físico e ingeniero de sistemas de control, 1905-1982).

^{Figura\(\PageIndex{2}\): Función de frecuencia-respuesta del sistema amortiguador-resorte de primer orden}

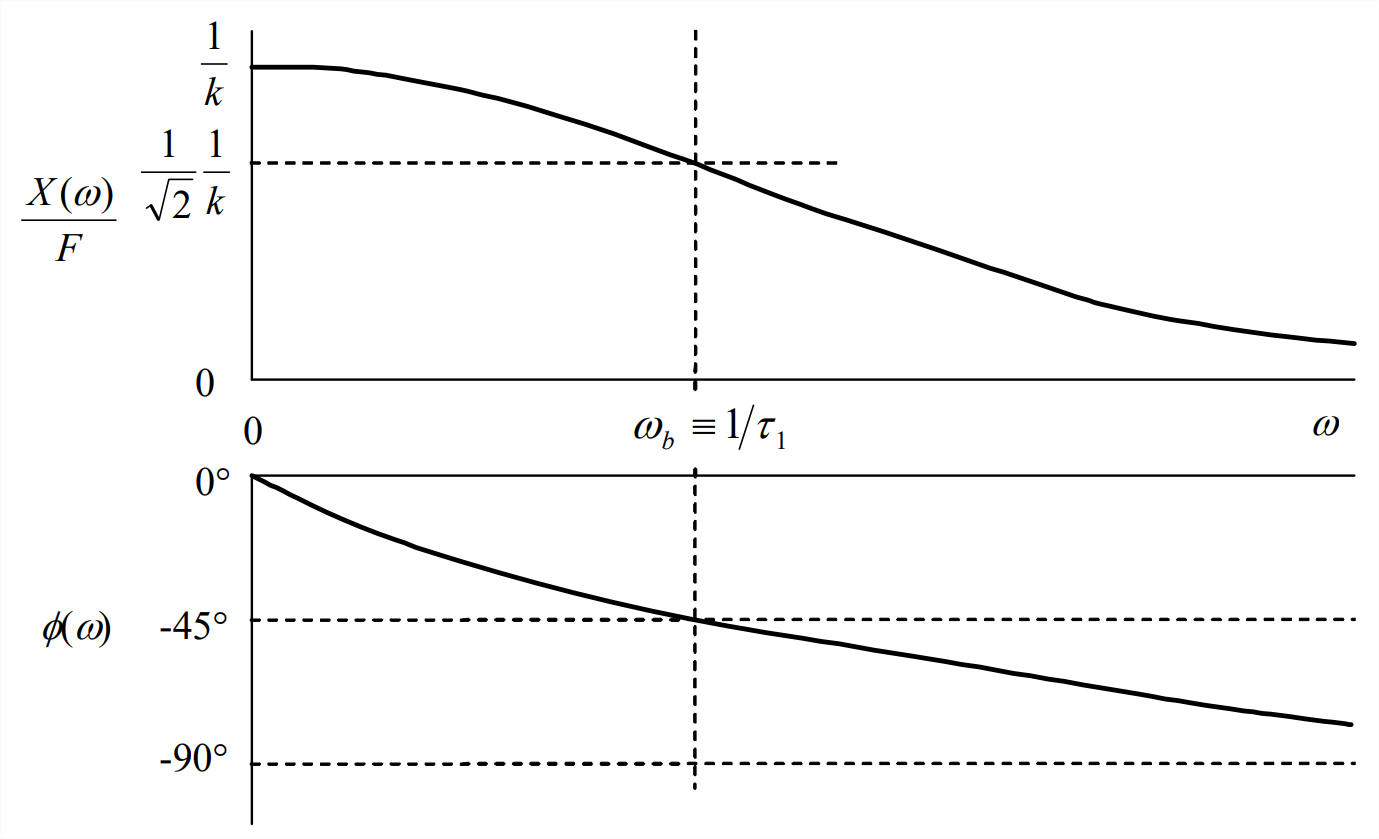
La frecuencia de ruptura\(\omega_{b} \equiv 1 / \tau_{1}\) se muestra explícitamente en la Figura\(\PageIndex{2}\). No hay una “ruptura” obvia en las curvas de la Figura\(\PageIndex{2}\); pero sí existe una ruptura, cuya forma se revelará en la siguiente discusión.

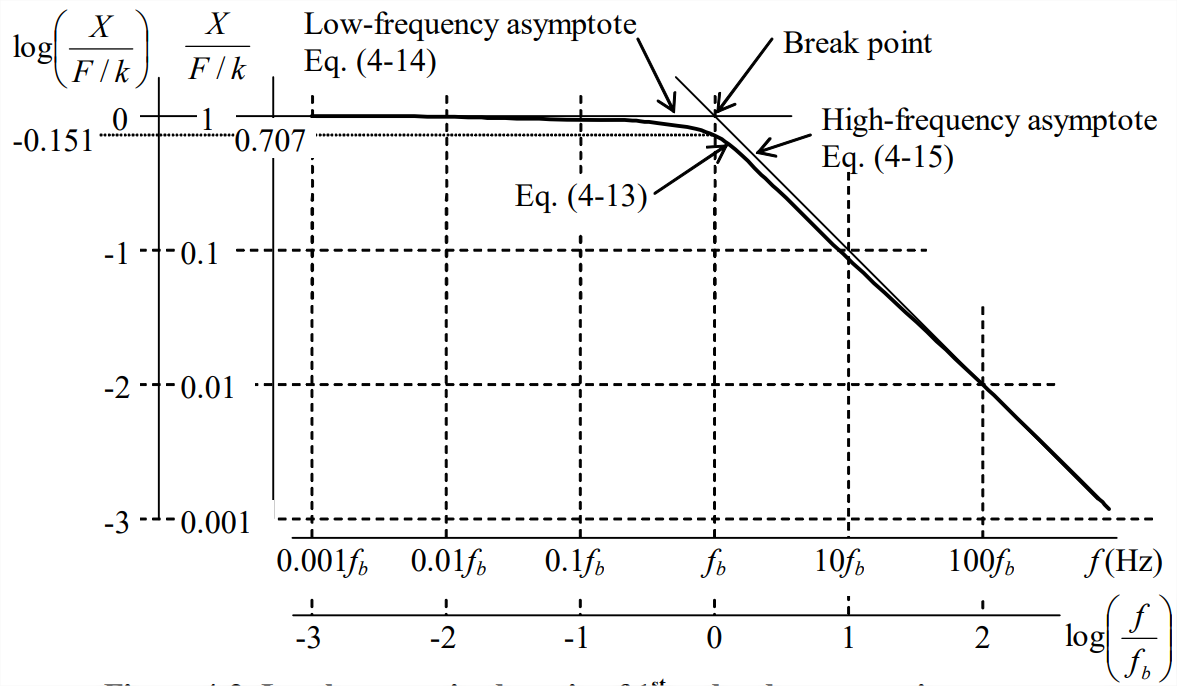
Para representar la respuesta de frecuencia en bandas anchas de frecuencia, la relación de magnitud y fase a menudo se grafican versus el logaritmo de frecuencia. Además, para permitir la posibilidad de rangos dinámicos muy grandes de respuesta de magnitud, la relación de magnitud en sí a menudo se traza en una escala logarítmica, haciendo de la relación de magnitud un gráfico logarítmico, donde “log” denota logaritmo a la base 10. En dicha gráfica, a menudo es posible construir asíntotas en línea recta que son útiles para describir la variación con la frecuencia de la magnitud. Para ilustrar esto para el sistema de ^primer orden, reescribimos la ecuación\(\ref{eqn:4.11}\) como una relación adimensional y, para mayor claridad de expresión, usamos la definición\(\omega_{b} \equiv 1 / \tau_{1}\), y luego tomamos el logaritmo:

\[\frac{X(\omega)}{F / k}=\frac{1}{\sqrt{1+\left(\omega \tau_{1}\right)^{2}}}=\frac{1}{\sqrt{1+\left(\omega / \omega_{b}\right)^{2}}}=\frac{1}{\sqrt{1+\left(f / f_{b}\right)^{2}}}\label{eqn:4.13a} \]

\[\log \left(\frac{X(\omega)}{F / k}\right)=\log \left(\frac{1}{\sqrt{1+\left(\omega / \omega_{b}\right)^{2}}}\right)=-\frac{1}{2} \log \left[1+\left(\frac{\omega}{\omega_{b}}\right)^{2}\right]=-\frac{1}{2} \log \left[1+\left(\frac{f}{f_{b}}\right)^{2}\right]\label{eqn:4.13b} \]

En las últimas versiones en los lados derecho de Ecuaciones\(\ref{eqn:4.13a}\) y\(\ref{eqn:4.13b}\), hemos utilizado\(\omega \equiv 2 \pi f\) y\(\omega_{b} \equiv 2 \pi f_{b}\) con el fin de expresar la ecuación en términos de frecuencia cíclica. La asíntota de baja frecuencia es el límite de la Ecuación\(\ref{eqn:4.13b}\) como la frecuencia\(\rightarrow\) 0 desde arriba:

\[\lim _{\omega \rightarrow 0}\left[\log \left(\frac{X(\omega)}{F / k}\right)\right]=-\frac{1}{2} \log (1)=0\label{eqn:4.14} \]

La asíntota de alta frecuencia es el límite de la Ecuación\(\ref{eqn:4.13b}\) como la frecuencia\(\rightarrow\inf\) desde abajo:

\[\lim _{\omega \rightarrow \infty}\left[\log \left(\frac{X(\omega)}{F / k}\right)\right]=-\frac{1}{2} \log \left[\left(\frac{\omega}{\omega_{b}}\right)^{2}\right]=-\log \left(\frac{\omega}{\omega_{b}}\right)=-\log \left(\frac{f}{f_{b}}\right)\label{eqn:4.15} \]

La figura\(\PageIndex{3}\) de la siguiente página es una gráfica log-log de Ecuaciones\(\ref{eqn:4.13a}\) y\(\ref{eqn:4.13b}\) que muestra las asíntotas Ecuación\(\ref{eqn:4.14}\) y Ecuación\(\ref{eqn:4.15}\). Observe que en la escala log-log, la asíntota de baja frecuencia es una buena aproximación para la función real en frecuencias\(f<f_{b_{j}}\), y la asíntota de alta frecuencia es una buena aproximación para la función real en frecuencias\(f>f_{b_{j}}\). La intersección de las dos asíntotas se denomina ruptura (o esquina) porque es un cambio en la pendiente de las aproximaciones asintóticas a la función real. Se denota la frecuencia de rotura (o esquina)\(f_b\). Para este sistema ^de primer orden a\(f_{b}=\omega_{b} / 2 \pi=1 /\left(2 \pi \tau_{1}\right)\), la magnitud de respuesta se reduce a\(1 / \sqrt{2}\) de su valor estático (\(f\)= 0), y la fase es de -45° (ver también Figura\(\PageIndex{2}\)).

La asíntota de alta frecuencia en la Figura\(\PageIndex{2}\) amerita algún comentario adicional. Obsérvese que su pendiente en la escala log-log es igual a —1, es decir, la magnitud se contrae una década (orden de magnitud) por cada década de incremento en la frecuencia. Las relaciones de magnitud de respuesta de frecuencia a menudo se dan en decibelios (dB), especialmente en acústica para el nivel de presión sonora. Una relación de magnitud en decibelios se define como 20 ×\(\log\) (relación de magnitud). Si la relación de magnitud en la Figura se\(\PageIndex{2}\) hubiera trazado en decibelios versus\(\log\) (frecuencia), entonces la pendiente de la asíntota de alta frecuencia sería —20; esto a menudo se conoce como un rolloff de 20 dB/década de la relación de magnitud.

^{Otra observación que vale la pena hacer, especialmente de la Figura\(\PageIndex{2}\), es que el sistema estándar de primer orden considerado aquí se comporta como un filtro de paso bajo suave: el sistema responde con mayor sensibilidad a la excitación a frecuencias por debajo de la frecuencia de ruptura, siendo la magnitud de la respuesta} aproximadamente igual a la respuesta estática. Sin embargo, a frecuencias de excitación por encima de la frecuencia de interrupción, el sistema responde mucho menos sensiblemente, y la magnitud de la respuesta disminuye progresivamente a medida que aumenta la frecuencia de excitación.

^{Figura\(\PageIndex{3}\): Relación log-logarítmica de magnitud del sistema amortiguador-resorte de primer orden}