7.3: Respuesta de CI simple y respuesta escalonada de sistemas de segundo orden sin amortiguar

Encontramos en esta sección dos importantes soluciones de casos especiales de las Ecuaciones 7.2.4 y 7.2.5:

1. respuesta de condición inicial pura para entrada cero,\(u(t) = 0\) y
2. respuesta pura de paso con ambas condiciones iniciales siendo cero.

Para el caso de la respuesta de condición inicial pura (también llamada vibración libre), con\(u(t) = 0\), las ecuaciones 7.2.4 y 7.2.5 se convierten en

\[x(t)=x_{0} \cos \omega_{n} t+\frac{\dot{x}_{0}}{\omega_{n}} \sin \omega_{n} t, 0 \leq t\label{eqn:7.10} \]

Usemos una identidad trigonométrica [ver Ecuaciones 4.3.2, 4.3.4 y 4.3.5] para combinar las dos sinusoides de Ecuaciones\(\ref{eqn:7.10}\) en un solo término. La siguiente definición reducirá la escritura requerida y además resultará ser físicamente significativa:

\[x_{\max } \equiv \sqrt{x_{0}^{2}+\left(\dot{x}_{0} / \omega_{n}\right)^{2}}\label{eqn:7.11} \]

\[\Rightarrow \quad x(t)=x_{\max }\left[\cos \omega_{n} t \times\left(\frac{x_{0}}{x_{\max }}\right)-\sin \omega_{n} t \times\left(\frac{-\dot{x}_{0} / \omega_{n}}{x_{\max }}\right)\right] \nonumber \]

\[\Rightarrow \quad x(t)=x_{\max } \cos \left(\omega_{n} t+\phi\right), 0 \leq t, \quad \phi=\tan ^{-1}\left(\frac{-\dot{x}_{0} / \omega_{n}}{x_{0}}\right)\label{eqn:7.12} \]

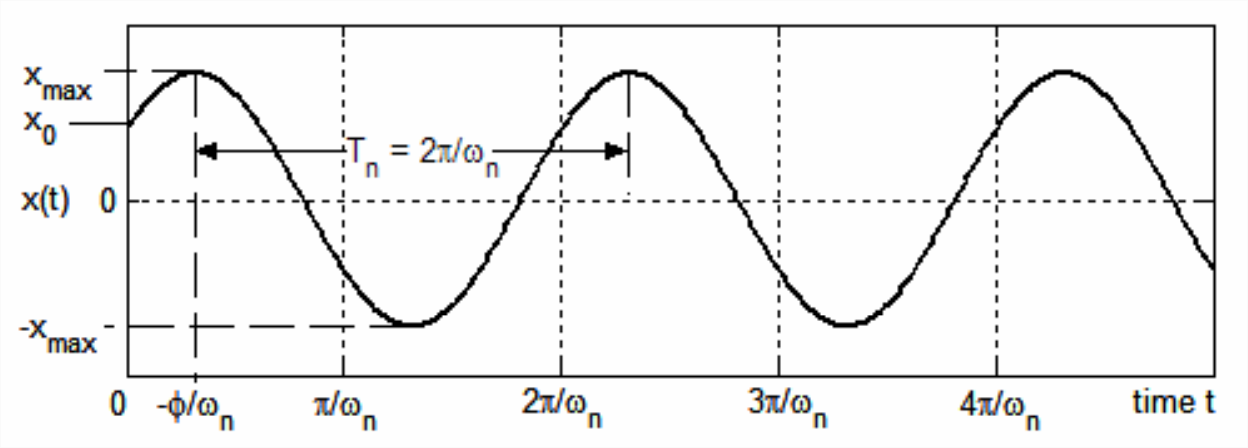
La Figura\(\PageIndex{1}\) es una gráfica anotada de la Ecuación de respuesta\(\ref{eqn:7.11}\) -Ecuación\(\ref{eqn:7.12}\) para los valores positivos de los CI,\(x_{0}>0\) y\(\dot{x}_{0}>0\). Claramente, la salida es una sinusoide pura de amplitud\(x_{\max }\) y ángulo de fase\(\phi\). Esta forma de respuesta se llama vibración libre, porque ocurre sin ninguna entrada forzada,\(u(t)\) = 0. La frecuencia circular de vibración es\(\omega_n\) rad/s, la frecuencia natural definida en la Ecuación 7.1.3. La frecuencia natural cíclica es\(f_{n}=\omega_{n} / 2 \pi\) ciclo/s (Hz), y el periodo natural anotado en la Figura\(\PageIndex{1}\) es\(T_{n}=1 / f_{n}=2 \pi / \omega_{n}\) s/ciclo. La vibración libre a la frecuencia natural es una de las características más importantes de los sistemas sin amortiguar y, de manera más realista, de los sistemas ligeramente amortiguados. Los sistemas amortiguados ^{de segundo} orden se discuten en el Capítulo 9.

Figura\(\PageIndex{1}\): Respuesta IC de un sistema de ^{segundo orden no} amortiguado

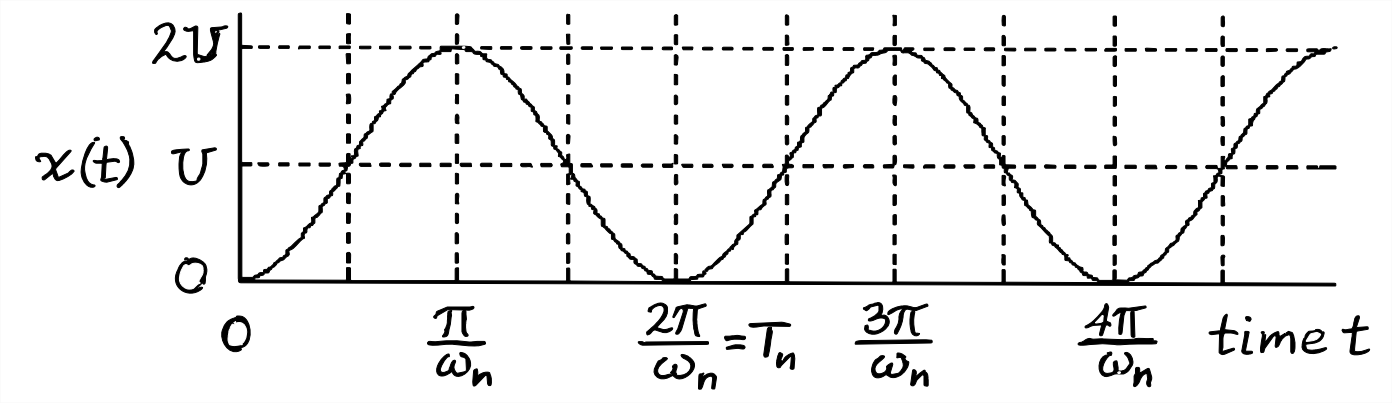
Para el caso de respuesta de paso puro, establecemos los CI en cero, y definimos la entrada para que sea una función de paso en el tiempo\(t\) = 0, con magnitud de paso\(U\):

\[u(t)=U H(t)\label{eqn:7.13} \]

La forma apropiada de la solución general a utilizar en este caso es la Ecuación 7.2.4,

\[x(t)=\omega_{n} \int_{\tau=0}^{\tau=t} \sin \omega_{n} \tau \times u(t-\tau) d \tau=\omega_{n} \int_{\tau=0}^{\tau=t} \sin \omega_{n} \tau \times U H(t-\tau) d \tau=\omega_{n} U \int_{\tau=0}^{\tau=t} \sin \omega_{n} \tau d \tau \nonumber \]

Aquí se utilizó la propiedad de la función unidad-paso que\(H(t-\tau)=1\) para\(t-\tau>0\) (de la Ecuación 2.4.2 y Figura 2.4.2); esta desigualdad obviamente se satisface por\(\tau\) encima de los límites de la integral definida. Para la mayoría de las aplicaciones de las integrales de convolución en las Ecuaciones 7.2.4 y 7.2.5, la forma en la Ecuación 7.2.5 es preferible porque el término integral\(u(t-\tau)\) en la Ecuación 7.2.4 suele ser difícil de interpretar y/o incómodo de manejar en la integración. Este caso, sin embargo, es una excepción ya que\(u(t-\tau)\) es fácil de interpretar y es extremadamente simple. Completar la integración da

\[x(t)=\omega_{n} U \int_{t=0}^{r=t} \sin \omega_{n} \tau d \tau=\omega_{n} U \int_{t=0}^{r=t}\left(\frac{-1}{\omega_{n}}\right) d\left(\cos \omega_{n} \tau\right)=-U\left[\cos \omega_{n} \tau\right]_{0}=-U\left(\cos \omega_{n} t-1\right) \nonumber \]

\[\Rightarrow \quad x(t)=U\left(1-\cos \omega_{n} t\right), 0 \leq t\label{eqn:7.14} \]

\(\ref{eqn:7.14}\)La ecuación se grafica para algunos ciclos de respuesta en la Figura\(\PageIndex{2}\). La respuesta es sinusoidal y periódica con el periodo natural del sistema\(T_{n}\), al igual que la respuesta IC de vibración libre. Sin embargo, Ecuación\(\ref{eqn:7.14}\) es respuesta forzada, y la entrada no\(u(t)\) es cero y constante para\(t > 0\), por lo que esta respuesta escalonada vibra alrededor de un valor medio distinto de cero (el valor de salida pseudo-estático\(x_{p s}=U\)), oscilando entre 0 y 2\(U\). En contraste, la respuesta IC de vibración libre de Ecuación\(\ref{eqn:7.12}\) y Figura\(\PageIndex{1}\) vibra alrededor del valor medio cero, oscilando entre\(-x_{\max }\) y\(+x_{\max }\).

Figura\(\PageIndex{2}\): Respuesta escalonada de un sistema de ^{segundo orden no} amortiguado