7.5: Movimiento Dinámico de un Sistema Mecánico Relativo a una Posición de Equilibrio Estático No Trivial; Diagrama Dinámico de Cuerpo Libre

Considere el sistema masa-resorte representado en la Figura\(\PageIndex{1}\) (en la página siguiente), que es representativo en muchos aspectos de algunos sistemas mecánicos reales. El sistema está orientado verticalmente en un campo de gravedad con aceleración de la gravedad\(g\). Además, supongamos que el resorte está enrollado de manera cerrada: un resorte de extensión helicoidal que, en su estado no estirado, se enrolla con sus espiras forzadas a entrar en contacto entre sí, de tal manera que\(F_i\) se requiere una fuerza de tensión inicial para romper el contacto de la bobina y permitir que el resorte comience estiramiento (Shigley y Mitchell, 1983, p. 449). La figura\(\PageIndex{1}\) ilustra tres estados posibles de dicho sistema. El peso de la masa\(m \) es\(W=m g\), y es un vector de fuerza constante que actúa hacia abajo a través del centro de gravedad de la masa. El resorte tiene rigidez constante\(k\) y tensión inicial\(F_i\), por lo que la ley del resorte es\(f_{y}=F_{i}+k y\) para\(f_{y} \geq F_{i}\), donde\(y\) está el resorte se estira verticalmente hacia abajo. El estado 1 de la figura\(\PageIndex{1}\) muestra la masa soportada estáticamente por una fuerza aplicada externamente\(W\) que actúa hacia arriba, con el resorte sin estirar y por lo tanto no ejercer fuerza sobre la masa. Definimos\(y_{t}(t)\) como el movimiento vertical total de la masa (positivo hacia abajo en este ejemplo, pero no necesariamente siempre así) relativo a la posición del resorte no estirado. Ahora, si la fuerza hacia arriba aplicada externamente se reduce lentamente, el peso de la masa se transfiere gradualmente al resorte, y el resorte se estira (siempre que eso\(W>F_{i}\)), bajando la masa. El Estado 2 de la Figura\(\PageIndex{1}\) es el estado de equilibrio estático que resulta después de que la fuerza hacia arriba aplicada externamente se contrae a cero, con el resorte estirado por la cantidad\(y_{s}\) desde la posición Estado 1. A partir del FBD del Estado 2, la ecuación de equilibrio de fuerza estática vertical es

\[F_{i}+k y_{s}=W \quad \Rightarrow \quad y_{s}=\frac{W-F_{i}}{k}, \text { for } W \geq F_{i}\label{eqn:7.15} \]

El Estado 3 de la Figura\(\PageIndex{1}\) es una condición de respuesta dinámica, con la fuerza dinámica\(f_{y}(t)\) que actúa sobre la masa. Definimos la posición dinámica\(y_{d}(t)\) como el movimiento relativo a la posición de equilibrio estático,\(y_{s}\) de la Ecuación\(\ref{eqn:7.15}\). Vemos de la Figura\(\PageIndex{1}\) que la traslación total (desde la posición de resorte no estirado) y la aceleración asociada son

\[y_{t}(t)=y_{s}+y_{d}(t) \Rightarrow \ddot{y}_{t}(t)=\ddot{y}_{d}(t)\label{eqn:7.16} \]

La ecuación de aceleración refleja la constancia de\(y_s\). Usemos el FBD para el Estado 3 para escribir la ^2ª ley de Newton para la traducción vertical:

\[\Sigma(\text { Forces })_{y}=m \ddot{y}_{t}=f_{y}(t)+W-\left(F_{i}+k y_{t}\right) \Rightarrow m \ddot{y}_{t}+k y_{t}=f_{y}(t)+W-F_{i}\label{eqn:7.17} \]

Ahora usa la ecuación\(\ref{eqn:7.16}\) para eliminar\(y_{t}(t)\) de la ecuación\(\ref{eqn:7.17}\):

\[m \ddot{y}_{d}+k\left(y_{s}+y_{d}\right)=f_{y}(t)+W-F_{i}\label{eqn:7.18} \]

A continuación, eliminar\(k y_{s}=W-F_{i}\), Ecuación\(\ref{eqn:7.15}\), de la Ecuación\(\ref{eqn:7.18}\) para expresar la ODE en términos del movimiento relativo a la posición de equilibrio estático, la única variable dependiente,\(y_{d}(t)\):

\[m \ddot{y}_{d}+k y_{d}=f_{y}(t)\label{eqn:7.19} \]

Es obvio físicamente que la Ecuación\(\ref{eqn:7.19}\) es válida siempre que el movimiento dinámico hacia arriba no exceda el estiramiento elástico estático:\(y_{t}(t)=y_{s}+y_{d}(t)>0\), es decir,\(y_{d}(t)>-y_s\).

Figura\(\PageIndex{1}\): Posiciones estáticas y dinámicas de un peso suspendido, soportado por resorte

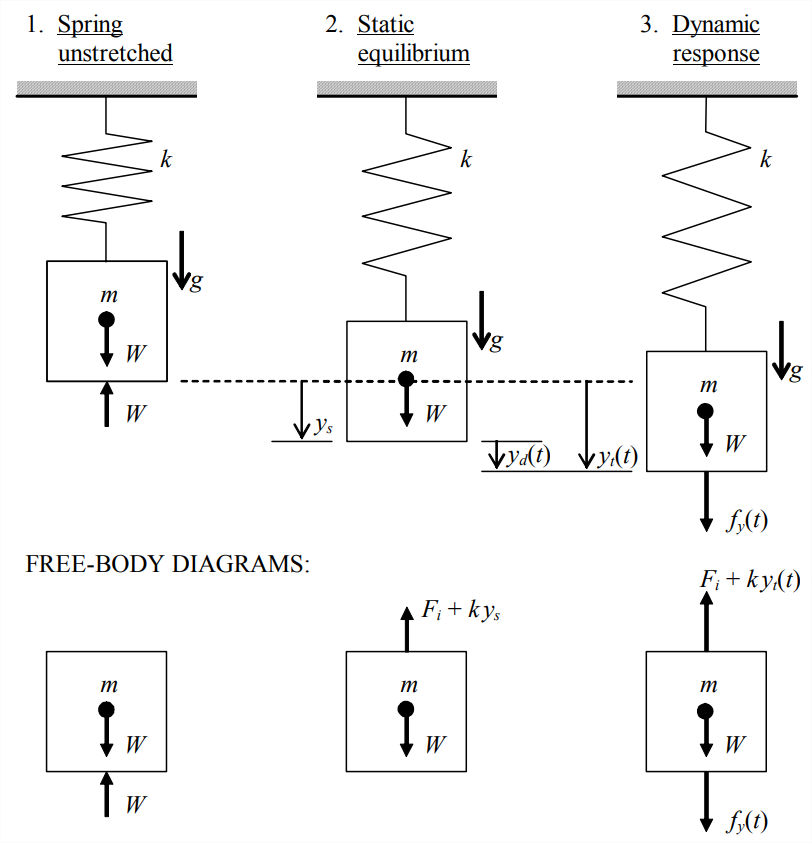
\(\ref{eqn:7.19}\)La ecuación es idéntica en forma a la Ecuación 7.1.2, que se aplica para un sistema de masa-resorte orientado horizontalmente, sin implicación de un resorte enrollado o gravedad. La única diferencia es que lo desconocido en la Ecuación no\(\ref{eqn:7.19}\) es el movimiento total, sino, en cambio, el movimiento relativo a la posición de equilibrio estático establecida por la gravedad y la tensión inicial del resorte. Consideremos el diagrama dinámico de cuerpo libre (DFBD) que se muestra\(\PageIndex{2}\) en la Figura de la página siguiente, que es similar al del Estado 3 de la Figura\(\PageIndex{1}\), pero sin peso\(W\) y con solo la fuerza elástica relativa a la posición de equilibrio estático. Estos cambios a partir del FBD del Estado 3 en la Figura\(\PageIndex{1}\) son equivalentes a eliminar\(k y_{s}=W-F_{i}\) de la Ecuación\(\ref{eqn:7.18}\) para obtener la Ecuación\(\ref{eqn:7.19}\). Claramente, aplicar la ^2ª ley de Newton a la Figura DFBD\(\PageIndex{2}\) conduce de nuevo, y mucho más fácilmente, a la Ecuación\(\ref{eqn:7.19}\). La conclusión importante aquí: si queremos resolver solo para el movimiento dinámico\(y_d(t)\) relativo a la posición de equilibrio estático, no el movimiento total relativo a la posición de resorte no deformado, entonces deberíamos usar un DFBD a partir del cual todas las influencias estáticas (peso y tensión inicial del resorte en este caso) han sido eliminados. El DFBD debe incluir solo fuerzas dinámicas (y/o momentos) relativos a la posición de equilibrio estático.

Figura\(\PageIndex{2}\): Diagrama dinámico de cuerpo libre

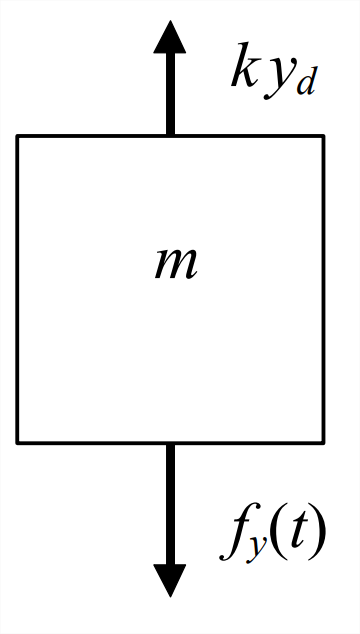
Esta conclusión es útil de manera más general porque, en muchas situaciones, estamos, en efecto, interesados principalmente en la respuesta dinámica relativa a la posición de equilibrio estático. Tarea Problema 7.3 es un ejemplo. Además, esta conclusión basada en el simple sistema masa-resorte de la Figura\(\PageIndex{1}\) tiene amplia aplicabilidad a otros sistemas mecánicos. Los temas de los Capítulos 11 y 12 son sistemas rotacionales más complejos y sistemas mecánicos de orden superior. Por lo general, es conveniente a la hora de analizar esos sistemas tratar solo con los DFBD y ODEs más simples que usamos cuando resolvemos solo para el movimiento dinámico relativo a la posición de equilibrio estático.

Sin embargo, existen al menos dos clases de sistemas mecánicos para los cuales debemos incluir (en FBD y ODEs de movimiento) los pesos de componentes masivos:

1. sistemas de péndulos para los que la gravedad proporciona un efecto de resorte, como el ejemplo simple de péndulo en la Sección 7.1 y el vehículo de balón-canasta de la tarea Problema 7.4;
2. sistemas para los que se definen condiciones iniciales y/o entradas dinámicas (fuerzas, momentos) en relación con el estado de resorte no deformado, por ejemplo, el contacto de aterrizaje del avión de la tarea Problema 7.5.