7.6: Introducción a las vibraciones de sistemas de parámetros distribuidos
- Page ID
- 84672
Un sistema como el sistema mecánico de masa-salpicadero y resorte de la Figura 7.1.1 a menudo se denomina sistema de parámetros grumados. Este término descriptivo se utiliza porque las características físicas esenciales son idealizadas para ser concentradas espacialmente: en la Figura 7.1.1, toda la masa se idealiza para residir en un elemento físico, toda la amortiguación en otro, y toda la rigidez en otro. Algunos sistemas de ingeniería se pueden modelar con precisión utilizando elementos agrupados idealizados; pero muchos sistemas reales no pueden, y estos últimos se denominan sistemas de parámetros distribuidos. Una viga estructural, como la que se muestra en la Figura 7-6 de la página siguiente, es un sistema mecánico prototípico de parámetros distribuidos. Es obvio que la masa de este haz no se concentra en un solo punto del espacio, sino que se distribuye por todo el volumen del haz. De igual manera, la flexibilidad de la viga no reside en un resorte discreto, sino que también se distribuye sobre todo el resorte. Finalmente, aunque hay muy poca amortiguación en este sistema en particular, también se distribuye por toda la viga en forma de “fricción” molecular dentro de la viga deformante y arrastre dinámico fluido en la superficie de la viga si la viga está sumergida en aire, otro gas o líquido.

La figura\(\PageIndex{2}\) es un registro real del movimiento del haz en la figura\(\PageIndex{1}\) en respuesta a una condición inicial particular: la punta de la viga se dobló hacia arriba estáticamente, luego se liberó 1.
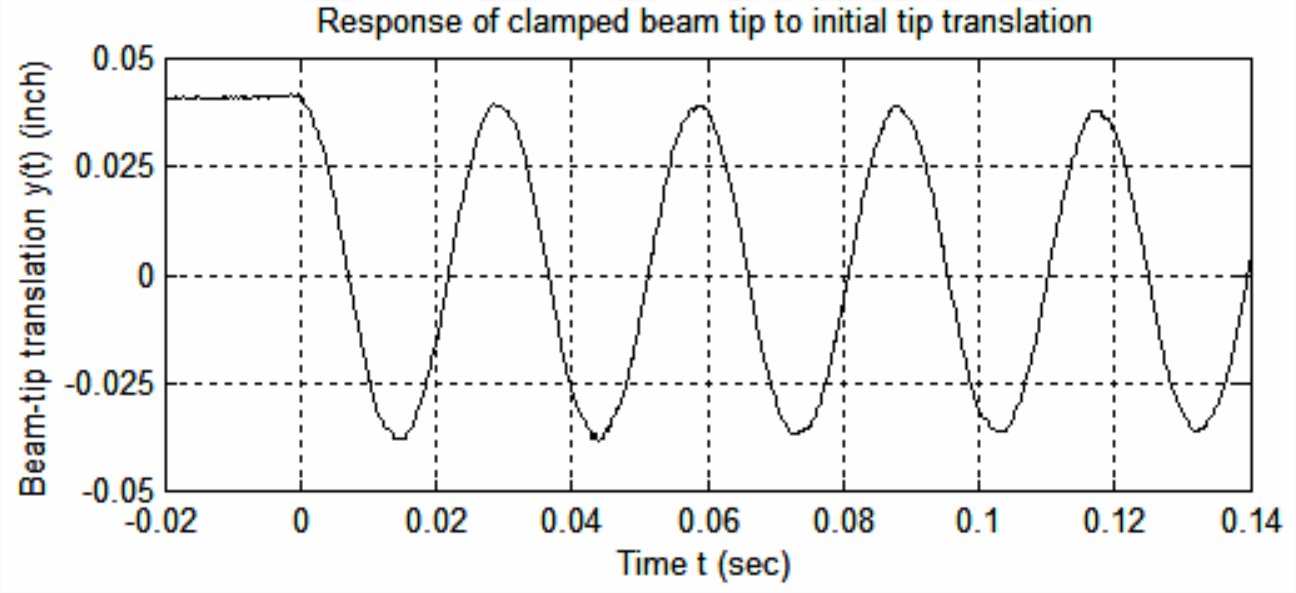
La respuesta temporal posterior fue directamente análoga a la respuesta teórica de CI mostrada en la Figura 7.3.1, con deflexión inicial positiva\(y_{0}>0\), pero velocidad inicial cero\(\dot{y}_{0}=0\),\(y(t)\) siendo traslación vertical, positiva hacia arriba, de la punta del haz con relación a la posición de equilibrio estático bajo carga por gravedad. \(\PageIndex{2}\)Obsérvese en la Figura que el carácter de la respuesta medida aparece muy cercano a lo predicho teóricamente en la Ec. (7-10) para un sistema de segundo orden sin amortiguar,\(y(t)=y_{0} \cos \omega_{n} t\). Sin embargo, podemos detectar mediante análisis detallado de los datos de la Figura\(\PageIndex{2}\) las siguientes diferencias muy pequeñas entre las respuestas reales y teóricas:
- i) ligeras reducciones de amplitud de un ciclo a otro, debido a la amortiguación muy ligera del sistema y a una liberación imperfecta del haz de su deformación inicial estática;
- (ii) una ligera excentricidad de la vibración con respecto a la posición de traslación cero, debido a un pequeño error de instrumentación, que es casi inevitable en las mediciones experimentales; y
- (iii) distorsión casi imperceptiblemente pequeña de la forma de onda relativa a un coseno perfecto.
(La distorsión más fácilmente observada aparece en la Figura\(\PageIndex{4}\), la cual se analiza a continuación). Esta pequeña distorsión de forma de onda ocurre porque el haz no es un sistema perfecto de parámetros agrupados de segundo orden; en realidad, el haz es, matemáticamente, un sistema de parámetros distribuidos mucho más complicado. Sin embargo, resulta que en muchas circunstancias, incluyendo esta en particular, podemos modelar aproximadamente estructuras de parámetros distribuidos como sistemas de segundo orden, con una precisión aceptable para muchos propósitos de ingeniería.
El estudio cuidadoso de los datos experimentales en la Figura\(\PageIndex{2}\) muestra que el tiempo entre dos picos sucesivos cualesquiera de la señal de respuesta, el “periodo” de vibración amortiguada, es\(T_{d}\approx\) 0.029 4 s. El sistema de la Figura\(\PageIndex{1}\) está amortiguado, por lo que no\(T_d\) es un verdadero periodo “natural” sin amortiguar. Sin embargo, las soluciones teóricas para modelos matemáticos predicen que un período medido como este para un sistema muy ligeramente amortiguado es casi igual, para todos los fines prácticos, al período natural verdadero. Por lo tanto, en los problemas de ejemplo a continuación, asumiremos que el periodo medido es el periodo natural del sistema, por lo que la frecuencia natural no amortiguada es de\(f_{n} \approx 1 / T_{d}=\) 34.0 Hz.
La figura\(\PageIndex{3}\) ilustra la distribución espacial del haz que vibra después del mismo tipo de condición inicial que la de la figura\(\PageIndex{2}\), pero con una magnitud de deformación mucho mayor. Para esta foto de borde encendido, el obturador de la cámara digital se abrió por\(\frac{1}{4}\) segundo, tiempo durante el cual el haz vibró a través de 8+ ciclos completos. Los límites superior e inferior de deformación dinámica aparecen como líneas curvas bastante distintas contra el fondo oscuro en la foto, mientras que los estados intermedios de deformación aparecen como un desenfoque. Esto ocurre porque la velocidad del movimiento fue cero en las deformaciones extremas; por lo tanto, los fotositios de la cámara digital fueron expuestos durante tiempos desproporcionadamente más largos a las deformaciones extremas que a las deformaciones intermedias.

Ejemplo\(\PageIndex{1}\): A Calculation of the "Effective" Tip Mass of the Vibrating Beam
Considera el sistema de Figura\(\PageIndex{1}\). Al cargar la viga estáticamente con pequeños pesos calibrados que cuelgan de la punta de la viga, y midiendo la desviación vertical de la punta del haz resultante con el sensor de proximidad, los estudiantes determinaron que una constante de rigidez promedio “efectiva” de la punta del haz\(k_{E}=7.86\) era lb/pulgada. Con esta rigidez y la frecuencia natural medida\(f_{n}\) = 34.0 Hz, podemos inferir un valor para la masa de punta “efectiva” de la Ecuación 7.1.3 en la forma
\[m_{E}=\frac{k_{E}}{\omega_{n}^{2}}=\frac{k_{E}}{\left(2 \pi f_{n}\right)^{2}}=\frac{7.86 \mathrm{lb} / \mathrm{inch}}{\left(2 \pi \times 34.0 \mathrm{s}^{-1}\right)^{2}}=1.72 \mathrm{e}-4 \mathrm{lb}-\mathrm{s}^{2} / \mathrm{inch} \nonumber \]
Es conveniente realizar una verificación de plausibilidad de este resultado, sobre todo porque a la mayoría de nosotros nos resulta difícil relacionarnos intuitivamente con valores de masa que se expresan en el sistema estructural tradicional de unidades (ver Sección 3-1). Los estudiantes midieron el voladizo de 10.00 pulgadas de la viga de aluminio uniforme en la Fig. 7-6 para pesar Wb = 0.230 lb, y midieron el peso del pequeño objetivo de acero en la punta de la viga como 0.13 oz = 0.0081 lb. Por lo tanto, la masa total de la viga más el objetivo es
\[m_{T}=W_{T} / g=(0.238 \mathrm{lb}) \div\left(386.1 \mathrm{inch} / \mathrm{s}^{2}\right)=6.16 \mathrm{e}-4 \mathrm{lb}-\mathrm{s}^{2} / \mathrm{inch} \nonumber \]
La relación de masa es\(m_{E} / m_{T}\) = 0.28. A la vista de la foto de la viga vibratoria\(\PageIndex{3}\), Figura, parece físicamente plausible que aproximadamente el 28% de la masa estructural total se volviera efectivamente en la vibración. Esto termina Ejemplo Problema\(\PageIndex{1}\).
Ejemplo\(\PageIndex{2}\): Calculations Based Upon Ideal Theory, Normal DImensions, and Standard Material Constants
Calculemos una estimación de la frecuencia natural del sistema de haces de la Figura\(\PageIndex{1}\) usando la Ecuación 7.1.3 en la forma\(f_{n}=\frac{1}{2 \pi} \sqrt{k_{E} / m_{E}}\). En este cálculo, supongamos que no tenemos datos medidos de hardware o instrumentación real, es decir, que solo tenemos el tipo de información que normalmente estaría disponible en la fase de diseño preliminar de un proyecto de ingeniería, incluso antes de que se fabrique un prototipo.
Solución
Primero, calculemos la constante teórica efectiva de rigidez\(k_E\). De sus cursos y libros de texto sobre el comportamiento estructural estático, es posible que esté familiarizado con la deformación bajo carga de elementos estructurales, como vigas uniformes (prismáticas) y ejes que se fabrican a partir de materiales homogéneos, isotrópicos y linealmente elásticos. La teoría relevante para la situación actual es la de una viga en voladizo (idealmente libre). De cualquier libro de texto con las palabras “mecánica de los materiales” o “resistencia de los materiales” en su título 2, se puede encontrar que la rigidez efectiva en la punta de una viga en voladizo uniforme es\(k_{E}=3 E I / L^{3}\), en la que\(E\) se encuentra el módulo de elasticidad del material,\(I\) es la 2ª momento de área (también llamado momento de inercia de área) de la sección transversal de la viga, y\(L\) es la longitud en voladizo de la viga. Para la viga de la Figura\(\PageIndex{1}\), usemos el módulo elástico estándar (en cálculos de diseño preliminar) para aluminio:\(E\) = 10.0e+6 lb/pulgada 2. Las dimensiones nominales de la sección transversal rectangular de la viga son ancho\(b\) = 2.00 pulgadas y profundidad\(h\) = 1/8 pulgada, para lo cual el momento teórico del área 2nd es\(I=b h^{3} / 12\) = 3.255e−4 pulgadas 4. Usando la longitud del voladizo de 10.00 pulgadas, calculamos la rigidez efectiva de la punta del haz para ser
\[k_{E}=\frac{3 \times\left(10.00 \times 10^{6} \mathrm{lb} / \mathrm{inch}^{2}\right) \times\left(3.255 \times 10^{-4} \mathrm{inch}^{4}\right)}{(10.00 \mathrm{inch})^{3}}=9.766 \mathrm{lb} / \mathrm{inch} \nonumber \]
A continuación, calculemos una masa efectiva de punta\(m_{E}\). Considere primero la vibración de una viga en voladizo uniforme ideal sola (es decir, sin una masa de punta concentrada como el blanco de acero que se muestra en la Figura\(\PageIndex{1}\)). La teoría más avanzada 3 muestra que, para tal haz desnudo, la masa efectiva de la punta que vibra a la frecuencia natural fundamental es 0.242 672 de la masa total del haz, que determinamos a continuación. El peso de una viga uniforme es\(W_{b}=w A L\), en la que\(w\) se encuentra la densidad de peso (peso por unidad de volumen), y el área de sección transversal de una viga rectangular es\(A=b h\). Usemos la densidad de peso estándar (en los cálculos de diseño preliminar) del aluminio,\(w\) = 0.1000 lb/inch 3, para que el peso de nuestra viga en voladizo ideal sea\(W_b\) = (0.1000 lb/inch 3)\(\times\) (\(\frac{1}{4}\)inch 2)\(\times\) 0.2500 lb. de ahí que el la masa efectiva de la punta de la viga desnuda sola es\(m_{b E}\) = (0.242 672\(\times W_{b} / g\) = 0.242 672\(\times\) (0.2500 lb)\(\div\) (386.1 pulgadas/s 2) = 1.571e−4 lb-s 2 /pulgada. Para obtener una estimación intuitivamente lógica de la masa total efectiva de la punta, agregamos a\(m_{b E}\) la masa del blanco de acero que está unido a la punta de la viga en la Figura\(\PageIndex{1}\):\(m_{E}=m_{b E}+(0.0081 \mathrm{lb}) \div\left(386.1 \mathrm{inch} / \mathrm{s}^{2}\right)=1.78 \mathrm{e}-4 \mathrm{lb}-\mathrm{s}^{2} / \mathrm{inch}\).
Finalmente, la frecuencia natural basada en la teoría ideal, las dimensiones nominales y las constantes materiales estándar es
\[f_{n}=\frac{1}{2 \pi} \sqrt{\frac{k_{E}}{m_{E}}}=\frac{1}{2 \pi} \sqrt{\frac{9.77 \mathrm{lb} / \mathrm{inch}}{1.78 \times 10^{-4} \mathrm{lb} \cdot \mathrm{s} ^{2} / \mathrm{inch}}}=37.3 \mathrm{Hz} \nonumber \]
Ver tarea Problema 7.8 para un análisis de la discrepancia entre esta frecuencia natural calculada y el valor medido de 34.0 Hz. Esto termina Ejemplo Problema 7-2.
El sistema de haz cerrado de la Figura\(\PageIndex{1}\) parece comportarse muy parecido a un sistema de segundo orden cuando responde dinámicamente a una simple desviación estática inicial de la punta de la viga. Sin embargo, cuando se somete a la mayoría de los otros tipos posibles de excitación, su respuesta dinámica es más complicada. Por ejemplo, cuando la punta de la viga se tocó ligeramente hacia arriba con un pequeño martillo, la punta se movió verticalmente como se muestra en la Figura\(\PageIndex{4}\), página siguiente.
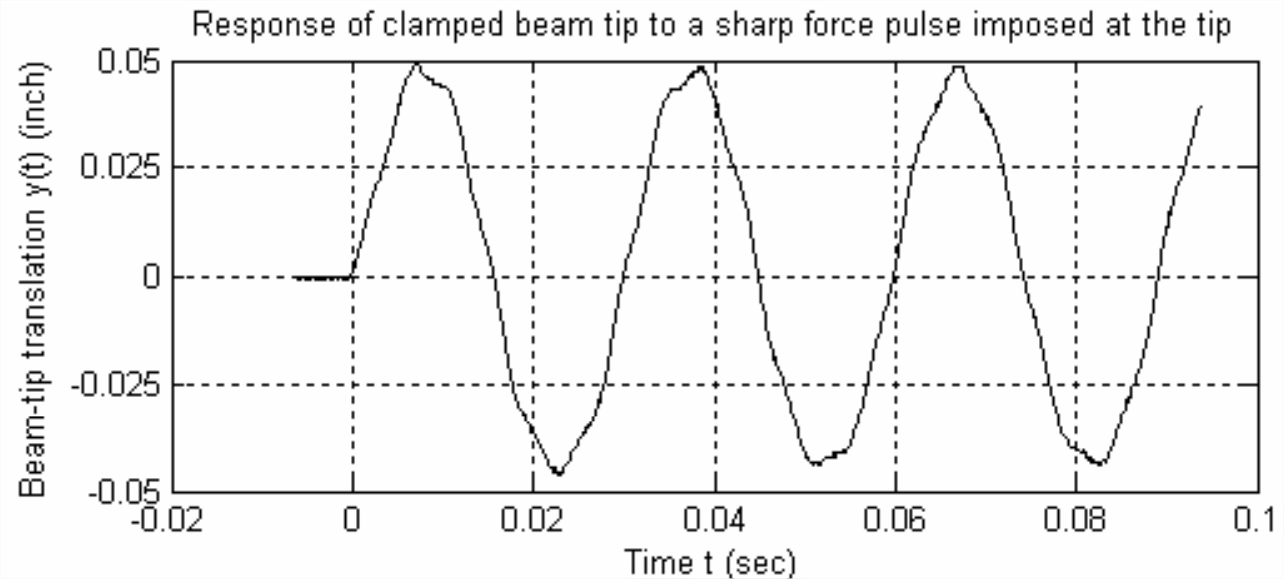
La fuerza de entrada que estimuló la respuesta de la Figura\(\PageIndex{4}\) fue aproximadamente un pulso de medio seno (como se describe en las Secciones 1.5 y 1.6) de muy corta duración relativa al periodo ligeramente amortiguado de este sistema,\(T_{d} \approx\) 0.029 4 s. En el Capítulo 8, se desarrolla teoría que demuestra que, si el sistema fuera un verdadero sistema de segundo orden sin amortiguar, entonces la respuesta de tiempo a tal pulso tendría casi una forma de onda sinusoidal perfecta, comenzando en el tiempo\(t\) = 0 s. Sin embargo, la forma de onda en la Figura\(\PageIndex{4}\) es bastante diferente de una forma de onda sinusoidal perfecta; de hecho, está más cerca de ser la suma de muchos sinusoides, en el espíritu general de una serie de Fourier, pero sin la propiedad de la serie de Fourier de que todas las sinusoides de series superiores tienen frecuencias que son múltiplos enteros de la frecuencia de la primera sinusoide (fundamental) 4. En el caso de la Figura\(\PageIndex{4}\), el movimiento total consiste principalmente en una primera sinusoide con frecuencia 34.0 Hz, más una segunda sinusoide de menor amplitud con frecuencia aproximadamente 215 Hz. El movimiento a 34.0 Hz representa el primer modo (fundamental) de vibración, y el movimiento a 215 Hz representa el segundo modo de vibración.
De hecho, el sistema de haz de la Figura\(\PageIndex{1}\) tiene muchos más de dos modos de vibración, cada uno con una frecuencia característica superior a la del modo anterior. Los modos tercero y superior no son evidentes en la Figura\(\PageIndex{4}\) solo porque el estímulo de pulso particular aplicado en este caso no excitó notablemente esos modos superiores; sin embargo, podrían ser excitados por cualquier número de otros estímulos, como pulsos agudos aplicados en ubicaciones particulares, sonido de alta frecuencia- ondas de presión, etc. En realidad, cada sistema de parámetros distribuidos es un sistema de orden superior a -2 y, aunque solo sea ligeramente o moderadamente amortiguado, tiene muchos modos de vibración. Por ejemplo, cada instrumento musical acústico es un sistema fluido o estructural de parámetros distribuidos cuya calidad sonora distintiva es consecuencia directa de sus modos particulares de vibración 5. Sin embargo, a excepción de esta breve introducción descriptiva, el tema de los sistemas de parámetros distribuidos está fuera del alcance de este libro. El tema de los modos de vibración vuelve a aparecer en el Capítulo 12, que trata de sistemas de parámetros abultados sin amortiguar, de 4º orden, que tienen dos modos de vibración.
Observe a partir de la Figura\(\PageIndex{4}\) que la respuesta de traslación del sistema de haz de la Figura todavía\(\PageIndex{1}\) estaba dominada por el primer modo de vibración, aunque el estímulo punta-pulso también excitó el segundo modo, pero a una amplitud mucho menor que la del primer modo. En adelante en este libro, la única respuesta de cualquier sistema de parámetros distribuidos que consideraremos es la contribución del primer modo, y asumiremos que domina la respuesta total. De hecho, esta es a menudo una buena aproximación de ingeniería para sistemas estructurales de parámetros distribuidos que incluyen masas relativamente grandes concentradas espacialmente. Consideremos, por ejemplo, el sistema de la Figura\(\PageIndex{5}\), que es el mismo que el de la Figura\(\PageIndex{1}\) pero con la adición en la punta de la viga de un conjunto de masa concentrada que consta de dos imanes cerámicos y un espaciador de aluminio, y pesa 0.254 lb

Cuando la punta de la viga de la Figura\(\PageIndex{5}\) se tocó ligeramente hacia arriba con un pequeño martillo, la punta se movió verticalmente como se muestra en la Figura\(\PageIndex{6}\). La curva de respuesta de traslación de punta es una forma de onda sinusoidal muy limpia con casi ninguna distorsión discernible. La ausencia de distorsión significativa en la forma de onda significa que, para nuestros fines, este sistema haz-masa se comporta como un sistema de segundo orden, aunque sea un sistema de parámetros distribuidos.
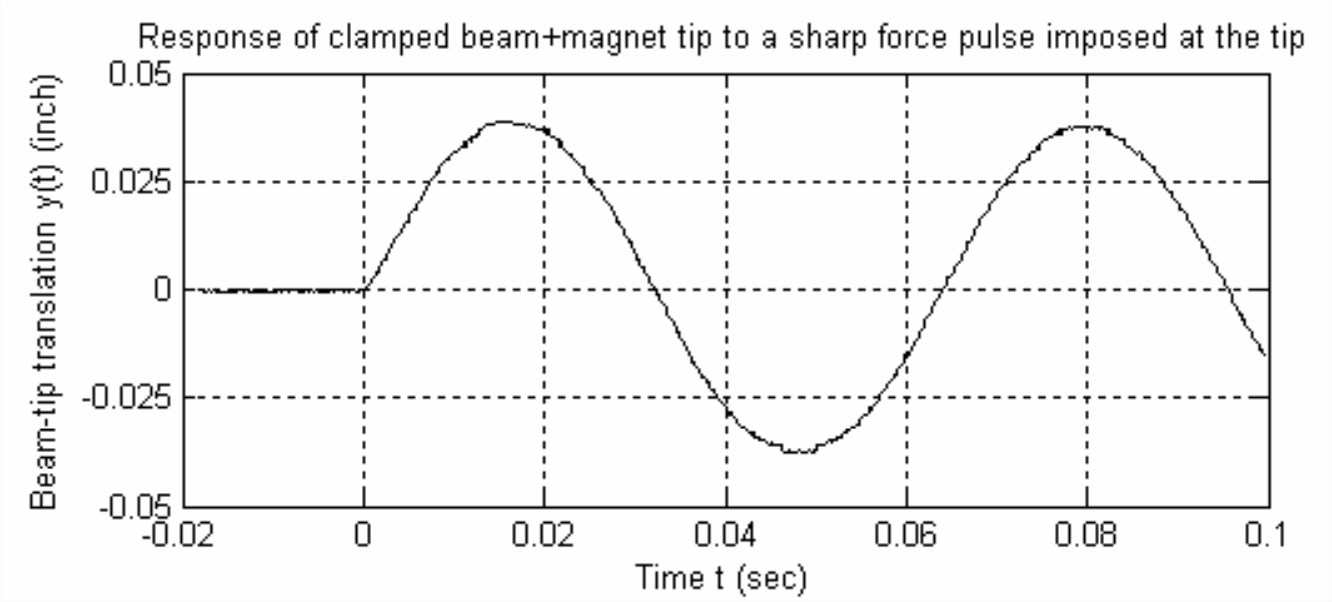
La adición de una cantidad relativamente grande de masa en la punta del haz reduce considerablemente la frecuencia de la forma de onda en la Figura\(\PageIndex{6}\) con relación a la frecuencia de 34.0-Hz de la forma de onda fundamental en las Figuras\(\PageIndex{2}\) y\(\PageIndex{4}\); un análisis cuidadoso de los datos en la Figura\(\PageIndex{6}\) muestra que el la frecuencia de vibración es\(f\) = 15.85 Hz.
Ejemplo\(\PageIndex{3}\): a Predictive Calculation of the Vibrational Frequency of the Beam-Mass System of Figure \(\PageIndex{5}\)
Supongamos que habíamos querido predecir la frecuencia del sistema haz-masa de la Figura\(\PageIndex{5}\) antes de ensamblar realmente el sistema y medir la frecuencia. El siguiente es un enfoque intuitivamente lógico, aunque no necesariamente teóricamente riguroso. Siempre que la viga sujeta se deforme linealmente bajo carga, la adición de masa y peso a la punta de la viga no debe alterar la constante de rigidez de la viga, por lo que usamos la misma rigidez efectiva medida en la punta de la viga que la del Ejemplo Problema 7-1,\(k_E\) = 7.86 lb/pulgada. Como se indicó anteriormente, el conjunto de masa concentrada que se agregó a la punta de la viga pesa 0.254 lb. Para obtener la masa total efectiva de la punta vibratoria, parece razonable sumar este valor y la masa efectiva de la punta de la viga desnuda más el blanco de acero, como se determina en el Ejemplo Problema 7-1. Así, encontramos la masa efectiva total\(m_E\) = 0.254 lb/ (386.1 pulgadas/s^2) + 1.72e−4 lb\(\cdot\) s 2 /pulgada = 8.30e−4 lb\(\cdot\) s 2 /pulg. Finalmente, calculamos la frecuencia natural predicha para ser
\[f_{n}=\frac{1}{2 \pi} \sqrt{\frac{k_{E}}{m_{E}}}=\frac{1}{2 \pi} \sqrt{\frac{7.86 \mathrm{lb} / \mathrm{inch}}{8.30 \times 10^{-4} \mathrm{lb} \cdot \mathrm{s} ^{2} / \mathrm{inch}}}=15.5 \mathrm{Hz} \nonumber \]
Esta frecuencia natural predicha es menor que el valor real medido de 15.85 Hz por un margen que es inesperadamente grande, presumiendo que todos los supuestos subyacentes a la teoría son válidos. Esto sugiere que la rigidez efectiva real durante la respuesta dinámica de la Figura\(\PageIndex{6}\) fue mayor a 7.86 lb/pulgada. Esto es bastante posible, ya que los estudiantes midieron la constante de rigidez efectiva promedio de la punta de la viga para ser de 7.86 lb/pulgada sobre un rango de deformación descendente muy pequeña de la viga, pero también observaron que la rigidez local (pendiente de la curva de carga versus deflexión) aumentó progresivamente a medida que aumentaba la deformación hacia abajo. Observe en las Figuras\(\PageIndex{1}\) y\(\PageIndex{5}\) en el extremo sujetado de la viga que parece haber un pequeño hueco entre el borde de la placa de sujeción superior de acero y la superficie superior de la viga; aunque no se ve claramente en estas fotos, existe un espacio similar entre la sujeción inferior placa de acero y la superficie inferior de la viga. Estos huecos son más anchos cuando la viga no está deformada, pero a medida que la viga se deforma hacia abajo, la brecha inferior se cierra gradualmente, reduciendo así ligeramente la longitud efectiva de la viga\(L\) y con ello aumentando de manera más significativa su rigidez en la punta\(k_{E}=3 E I / L^{3}\),, del Ejemplo\(\PageIndex{2}\). La carga de gravedad estática del conjunto de masa concentrada que se muestra en la Figura\(\PageIndex{5}\) cerró el hueco inferior, con relación a su ancho en la Figura\(\PageIndex{1}\) sin el conjunto de masa concentrada. Por lo tanto, es probable que la rigidez promedio de la punta del haz durante la respuesta registrada en la Figura\(\PageIndex{6}\) fue mayor que la de las respuestas registradas en las Figuras\(\PageIndex{2}\) y\(\PageIndex{4}\). El soporte de sujeción real y la restricción de la viga de aluminio en este experimento claramente no es el borde ideal, perfectamente afilado y pared completamente rígida que la teoría elemental asume para una viga en voladizo.
1 En la práctica, este procedimiento a menudo se llama prueba de twang (también snapback, relajación de pasos y pruebas de desplumado) —ver tarea Problema 9.4 para una discusión más detallada.
2 Ejemplos de tales libros de texto, enumerados en la sección Referencias: Beer y Johnston, 1992; Hibbeler, 1997; y Timoshenko y Young, 1962.
3 Teoría a partir de, entre muchas fuentes posibles, los siguientes libros de texto sobre dinámica estructural que se enumeran en la sección Referencias: Bisplinghoff, et al. , 1955, Ejemplo 3-1; Craig, 1981, Ejemplo 10.3; Meirovitch, 1967, Sección 5-10; y Meirovitch, 2001, Ejemplo 8.4.
4 El tema de las series de Fourier se desarrolla en la mayoría de los libros de texto sobre cálculo avanzado (por ejemplo, Hildebrand, 1962, páginas 216-226) y en la mayoría de los libros de texto sobre ecuaciones diferenciales parciales elementales.
5 Si te interesa la física de los instrumentos musicales, consulta Cannon, 1967, Secciones 13.2-13.6, para una excelente introducción escrita por un ingeniero para estudiantes de ingeniería.


