8.1: Pulso plano

Última actualización
Guardar como PDF

Page ID: 84523

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

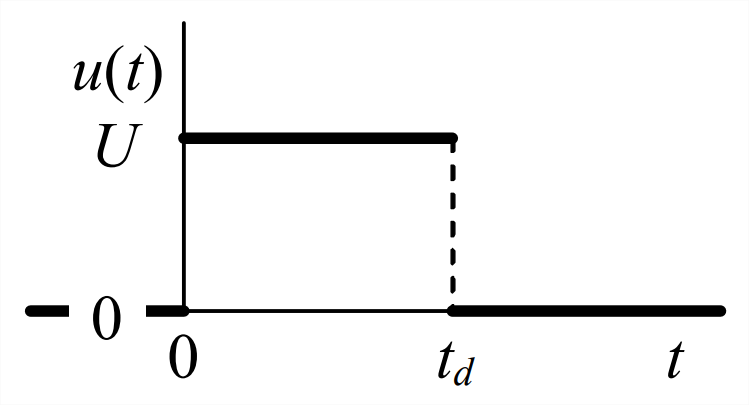
Esta es probablemente la forma más simple de entrada de duración limitada. Definimos el pulso plano inicialmente en forma de una cantidad de entrada general (estándar)\(u(t)\) que se puede usar con formas estándar de ODEs del sistema como\(\dot{x}+\left(1 / \tau_{1}\right) x=b u(t)\) para un sistema estable ^de primer orden y\(\ddot{x}+2 \zeta \omega_{n} \dot{x}+\omega_{n}^{2} x=\omega_{n}^{2} u(t)\) para sistemas ^{de segundo} orden. La figura\(\PageIndex{1}\) ilustra un pulso plano de duración\(t_d\). Se puede describir matemáticamente con el uso de dos funciones unidad-paso, tal como se define en la Sección 2.4:

\[u(t)=U\left[H(t)-H\left(t-t_{d}\right)\right]\label{eqn:8.1} \]

La transformada de Laplace de la Ecuación\(\ref{eqn:8.1}\), a partir de las Ecuaciones 2.4.4 y 2.4.5, es

\[L[u(t)]=U\left(\frac{1}{s}-\frac{e^{-s t_{d}}}{s}\right)=\frac{U}{s}\left(1-e^{-s t_{d}}\right)\label{eqn:8.2} \]

Ejemplo\(\PageIndex{1}\): Response to a Flat Pulse of an Undamped 2^nd Order System¹

El ODE para un sistema de orden 2 ^nd no amortiguado es\(\ddot{x}+\omega_{n}^{2} x=\omega_{n}^{2} u(t)\). Que las condiciones iniciales sean cero:\(x_{0}=0\),\(\dot{x}_{0}=0\). La solución general es entonces cualquiera de las dos formas integrales de convolución, las Ecuaciones 7.2.4 y 7.2.5. De esos dos, el más fácil de interpretar para el pulso plano discontinuo es la Ecuación 7.2.5, que con cero CI se convierte

\[x(t)=\omega_{n} \int_{\tau=0}^{\tau=t} \sin \omega_{n}(t-\tau) \times u(\tau) d \tau\label{eqn:8.3} \]

En lugar de usar Ecuación\(\ref{eqn:8.1}\) explícitamente, podemos observar la forma de Figura\(\PageIndex{1}\) y escribir Ecuación\(\ref{eqn:8.3}\) para dos intervalos de tiempo diferentes:

\ [x (t) =\ izquierda\ {\ comenzar {matriz} {c}
\ omega_ {n}\ int_ {\ tau=0} ^ {\ tau=t}\ sin\ omega_ {n} (t-\ tau)\ veces U d\ tau,\ quad 0\ leq t\ leq t_ {d}\
\ omega_ {n}\ int_ {tau_ =0} ^ {\ tau=t_ {d}}\ sin\ omega_ {n} (t-\ tau)\ veces U d\ tau+\ omega_ {n}\ int_ {\ tau=t_ {d}} ^ {\ tenso=t}\ sin\ omega_ {n} (t-\ tau)\ veces 0 d\ tau,\ quad t_ {d}\ leq t
\ end {array}\ right. \ label {eqn:8.4}\]

La segunda integral para\(t_{d} \leq t\) es obviamente cero. Esto nos deja con una sola integral para cada intervalo de tiempo, teniendo cada integral el mismo integrando y límite inferior. Sin embargo, las integrales tienen diferentes límites superiores, así que denotemos un límite superior general como\(T\), y evaluemos esa integral común con el uso de la variable de cambio de integración\(\lambda=t-\tau \Rightarrow d \lambda=-d \tau\):

\[\int_{\tau=0}^{\tau=T} \sin \omega_{n}(t-\tau) d \tau=\int_{\lambda=t}^{\lambda=t-T} \sin \omega_{n} \lambda(-d \lambda)=\frac{1}{\omega_{n}} \int_{\lambda=t}^{\lambda=t-T} d\left(\cos \omega_{n} \lambda\right)=\frac{1}{\omega_{n}}\left[\cos \omega_{n}(t-T)-\cos \omega_{n} t\right] \nonumber \]

Límite superior\(T ≡ t\) para de Ecuación\(\ref{eqn:8.4}\), y\(T \equiv t_{d}\) para\(t_{d} \leq t\), por lo tanto, sustituir el resultado de integración en Ecuación\(\ref{eqn:8.4}\) da las ecuaciones finales,

\ [x (t) =\ izquierda\ {\ comenzar {matriz} {l}
U\ izquierda (1-\ cos\ omega_ {n} t\ derecha),\ quad 0\ leq t\ leq t_ {d}\\
U\ izquierda [\ cos\ omega_ {n}\ izquierda (t-t_ {d}\ derecha) -\ cos\ omega_ {n} t derecha\],\ quad t_ {d}\ leq t
\ end {array}\ right. \ label {eqn:8.5}\]

La ecuación\(\ref{eqn:8.5}\) para\(0 \leq t \leq t_{d}\) es solo la respuesta de paso simple de la Ecuación 7.3.8, como lógicamente debería ser. La inspección de la ecuación\(\ref{eqn:8.5}\) muestra que la respuesta\(x(t)\) es continua en\(t=t_{d}\); diferenciando ambas ecuaciones de respuesta, podríamos demostrar que el término velocidad\(\dot{x}(t)\) también es continuo en\(t=t_{d}\). De hecho, estas cantidades de respuesta deben ser continuas, porque la ecuación\(\ref{eqn:8.5}\) describe una respuesta física (por ejemplo, de un sistema masa-resorte). De hecho, podríamos resolver este problema de manera diferente desde el principio usando el requisito de continuidad junto con la Ecuación 7.3.8 de respuesta escalonada y la Ecuación 7.3.4 de respuesta IC. Step response La Ecuación 7.3.8 es válida de\(t=0\) a\(t=t_{d}\); entonces podríamos encontrar\(x\left(t_{d}\right)\) y a\(\dot{x}\left(t_{d}\right)\) partir de la respuesta de paso y usar esos valores como condiciones iniciales para que la solución IC sea válida para\(t \geq t_{d}\).

¹ Ver también tarea Problema 8.3 para una solución directa sencilla pero elegante a la vez de transformar Laplace de este problema y una ecuación de respuesta físicamente significativa.