8.4: Función Dirac Delta

Consideremos un proceso límite con el impulso plano de la Fig. 8.3.1, en cuyo proceso acortamos progresivamente la duración del pulso manteniendo constante la magnitud del impulso (el área sombreada), aumentando así progresivamente la magnitud de entrada,\(I_{U} / t_{d}\). Si llevamos el proceso al límite como\(t_{d} \rightarrow 0\) manteniendo\(I_{U}\) constante, entonces magnitud\(I_{U} / t_{d} \rightarrow \infty\). El proceso de límite se ilustra en la Figura\(\PageIndex{1}\). La función que resulta se denomina impulso ideal con magnitud\(I_{U}\), y se denota como\(u(t)=I_{U} \times \delta(t)\), en la que\(\delta(t)\) se llama la función delta de Dirac (después del físico matemático inglés Paul Dirac, 1902-1984) o la función unidad-impulso. La función de impulso ideal generalmente\(I_{U} \delta(t)\) se representa gráficamente mediante un piquete grueso a\(t\) = 0, como en la Figura\(\PageIndex{1}\). Con\(I_{U}=1\) en la Ecuación 8.3.1, una definición matemática formal de la función unidad-impulso es

\[\delta(t)=\lim _{t_{d} \rightarrow 0} \frac{1}{t_{d}}\left[H(t)-H\left(t-t_{d}\right)\right]\label{eqn:8.8} \]

Observe a partir de la Ecuación\(\ref{eqn:8.8}\) que la dimensión de\(\delta(t)\) es tiempo ^-1, ya que la unidad-paso es adimensional, por lo que la unidad típica de\(\delta(t)\) es s ^-1.

Figura\(\PageIndex{1}\): Impulso ideal

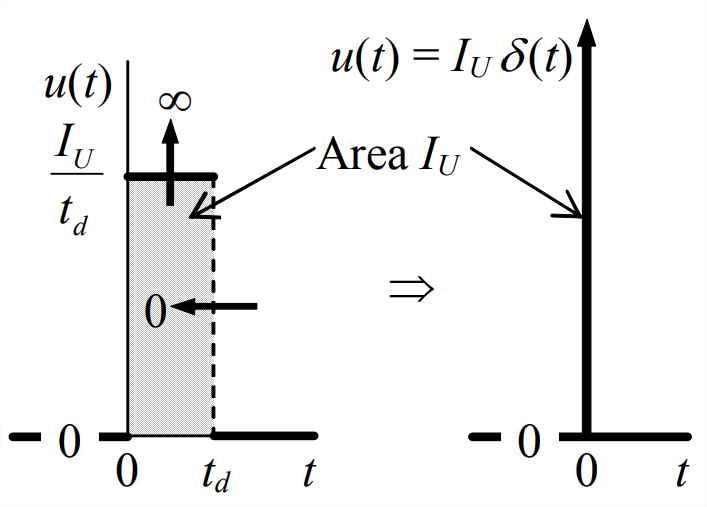
Por definición, el área bajo\(u(t)=I_{U} \delta(t)\) es igual\(I_{U}\), por lo que el área bajo\(\delta(t)\) es igual a 1 (de ahí el nombre unidad -función de impulso). Esta área unitaria bajo un impulso infinitamente corto sugiere un efecto importante de la función delta de Dirac en los integrandos. Para describir este efecto, definimos una función unidad-impulso más general,\(\delta\left(t-t_{\delta}\right)\), que alcanza su punto máximo infinitamente en algún momento arbitrario\(t_{\delta}\) que no es necesariamente cero; de lo contrario, la naturaleza de\(\delta\left(t-t_{\delta}\right)\) es idéntica a la de\(\delta(t)\) [de hecho,\(\delta(t)=\delta\left(t-t_{\delta}\right)\) para\(t_{\delta}\) = 0]. Ahora supongamos que tenemos alguna función física realista\(f(t)\) que se define a lo largo del intervalo de tiempo\(t_{1} \rightarrow t_{2}\), y supongamos que el tiempo\(t_{\delta}\) está dentro de este intervalo, como en la siguiente figura. Entonces el efecto de integración útil de\(\delta\left(t-t_{\delta}\right)\) es:

\[\int_{t=t_{1}}^{t=t_{2}} f(t) \delta\left(t-t_{\delta}\right) d t=f\left(t_{\delta}\right) \label{eqn:8.9} \]

Figura\(\PageIndex{2}\)

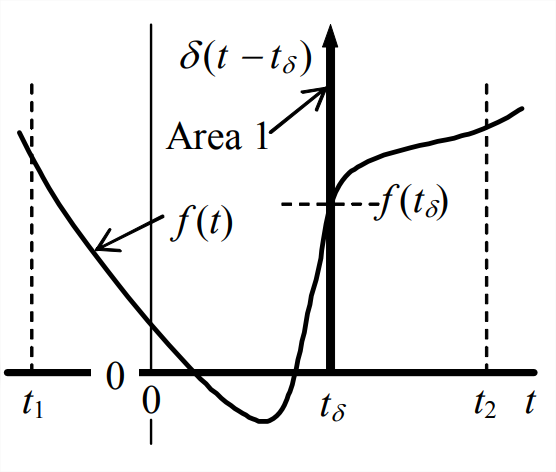
La ecuación\(\ref{eqn:8.9}\) establece que, como multiplicador dentro del integrando,\(\delta\left(t-t_{\delta}\right)\) esencialmente “selecciona” el valor de\(f(t)\) at\(t=t_{\delta}\). \(\ref{eqn:8.9}\)La ecuación de resultado es intuitivamente clara, y se puede probar de manera más rigurosa con la teoría de las llamadas funciones generalizadas (Lighthill, 1958).

Si el límite superior de integración en Ecuación\(\ref{eqn:8.9}\) es un tiempo arbitrario\(t>t_{\delta}\), entonces el resultado es una función de paso:

\[\int_{\tau=t_{1}}^{\tau=t>t_{\delta}} f(\tau) \delta\left(\tau-t_{\delta}\right) d \tau=f\left(t_{\delta}\right) H\left(t-t_{\delta}\right)\label{eqn:8.10} \]

Establecer\(f(\tau)=1\) en la ecuación\(\ref{eqn:8.10}\) conduce a una relación integral fundamental entre la función unidad-impulso y la función unidad-paso:

\[\int_{\tau=t_{1}}^{\tau=t>t_{\delta}} \delta\left(\tau-t_{\delta}\right) d \tau=H\left(t-t_{\delta}\right)\label{eqn:8.11} \]

Figura\(\PageIndex{3}\)

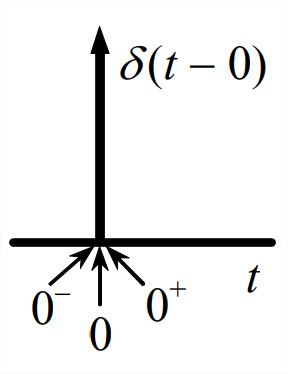
A continuación, usamos Ecuación\(\ref{eqn:8.9}\) para derivar la transformada de Laplace de la función delta\(\delta(t)= \delta(t-0)\). De acuerdo con la definición de la Ecuación 2.2.5, esta transformación se escribiría como\(L[\delta(t)]=\int_{t=0}^{t=\infty} e^{-s t} \delta(t-0) d t\); sin embargo, existe un problema con esta definición particular: at\(t\) = 0, que es el límite inferior del integrando (y el instante de valor inicial para la mayoría de las ODEs que resolvemos usando transformaciones de Laplace), la la función\(\delta(t-0)\) es nominalmente infinita, por lo que el significado de la integral es incierto. Elegimos eliminar la incertidumbre especificando que\(\delta(t-0)\) debe estar dentro de los límites de la integración. Para indicarlo claramente en notación, ahora definimos tres instantes de referencia diferentes, como se representa en el dibujo de la derecha:

1. \(t=0^{-}\), el instante justo antes de la actividad de la función impulsiva ideal, en y antes del cual\(\delta(t-0)=0\);
2. \(t = 0\), el instante en que\(\delta(t-0)\) actúa y es nominalmente infinito; y
3. \(t=0^{+}\), el instante justo después de la actividad de la función impulsiva ideal, en y después de la cual\(\delta(t-0)=0\).

En consecuencia, redefinimos la transformada de Laplace, más generalmente que en la Ecuación 2.2.5, como

\[L[f(t)]=\int_{t=0^{-}}^{t=\infty} e^{-s t} f(t) d t\label{eqn:8.12} \]

La distinción entre\(t=0\) y\(t=0^-\) en los límites inferiores de las Ecuaciones 2.2.5 y\(\ref{eqn:8.12}\), respectivamente, carece de sentido para todos los problemas considerados en este libro excepto aquellos en los que\(f(t)\) implica una función impulsiva ideal. Aplicación de Ecuaciones\(\ref{eqn:8.9}\) y\(\ref{eqn:8.12}\) ahora conduce a la transformación de Laplace de la función básica de impulso ideal:

\[L[\delta(t)]=\int_{t=0^{-}}^{t=\infty} e^{-s t} \delta(t-0) d t=e^{-s \times 0}=1\label{eqn:8.13} \]