8.7: Respuesta de impulso ideal de un sistema de segundo orden sin amortiguar

Última actualización
Guardar como PDF

Page ID: 84548

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El ODE para un sistema estándar de orden 2 ^nd no amortiguado es\(\ddot{x}+\omega_{n}^{2} x=\omega_{n}^{2} u(t)\). Deje que la función de entrada sea el impulso ideal\(u(t)=I_{U} \delta(t)\),, y que las condiciones iniciales previas al impulso sean\(x\left(0^{-}\right) \equiv x_{0}\),\(\dot{x}\left(0^{-}\right) \equiv \dot{x}_{0}\). Al igual que para el ^sistema de primer orden con excitación ideal-impulso en la Sección 8.5, resolveremos el problema actual mediante el enfoque convencional de transformación Laplace. Tenga en cuenta que usaremos la segunda forma derivada de la Ecuación 8.6.4:\(L[\ddot{f}]=s^{2} F(s)-s f\left(0^{-}\right)-\dot{f}\left(0^{-}\right)\). Con\(L[\delta(t)]=1\) la ecuación 8.4.6, los pasos de la solución son:

\[L[\mathrm{ODE}]: \quad s^{2} X(s)-s x_{0}-\dot{x}_{0}+\omega_{n}^{2} X(s)=b U(s)=\omega_{n}^{2} I_{U} \times 1 \nonumber \]

\[\Rightarrow \quad X(s)=\frac{\omega_{n}^{2} I_{U}+\dot{x}_{0}+s x_{0}}{s^{2}+\omega_{n}^{2}}=\left(\omega_{n} I_{U}+\frac{\dot{x}_{0}}{\omega_{n}}\right) \frac{\omega_{n}}{s^{2}+\omega_{n}^{2}}+x_{0} \frac{s}{s^{2}+\omega_{n}^{2}}\label{eqn:8.25} \]

\[\Rightarrow \quad x(t)=\left(\omega_{n} I_{U}+\frac{\dot{x}_{0}}{\omega_{n}}\right) \sin \omega_{n} t+x_{0} \cos \omega_{n} t, t \geq 0^{+}\label{eqn:8.26} \]

A riesgo de ser excesivamente repetitivo, enfatizamos que las discusiones en las Secciones 8.5 y 8.6 muestran que la Ecuación de respuesta\(\ref{eqn:8.26}\) es la solución post-impulso, ciertamente válida matemáticamente para\(t \geq 0^{+}\), pero no necesariamente correcta, en particular, para la inicial pre-impulso condiciones en\(t=0^-\).

La ecuación de solución se\(\ref{eqn:8.26}\) mantiene para un sistema general no amortiguado de ^segundo orden; adaptémoslo específicamente a un sistema masa-resorte, con cero condiciones iniciales, que es golpeado por un impulso ideal de fuerza que tiene magnitud\(I_{F}\), con unidades, por ejemplo, de N-s o lb-s. De la Ecuación 7.1.4, encontramos

\[u(t)=f_{x}(t) / k \Rightarrow I_{U} \delta(t)=I_{F} \delta(t) / k \Rightarrow I_{U}=I_{F} / k\label{eqn:8.27} \]

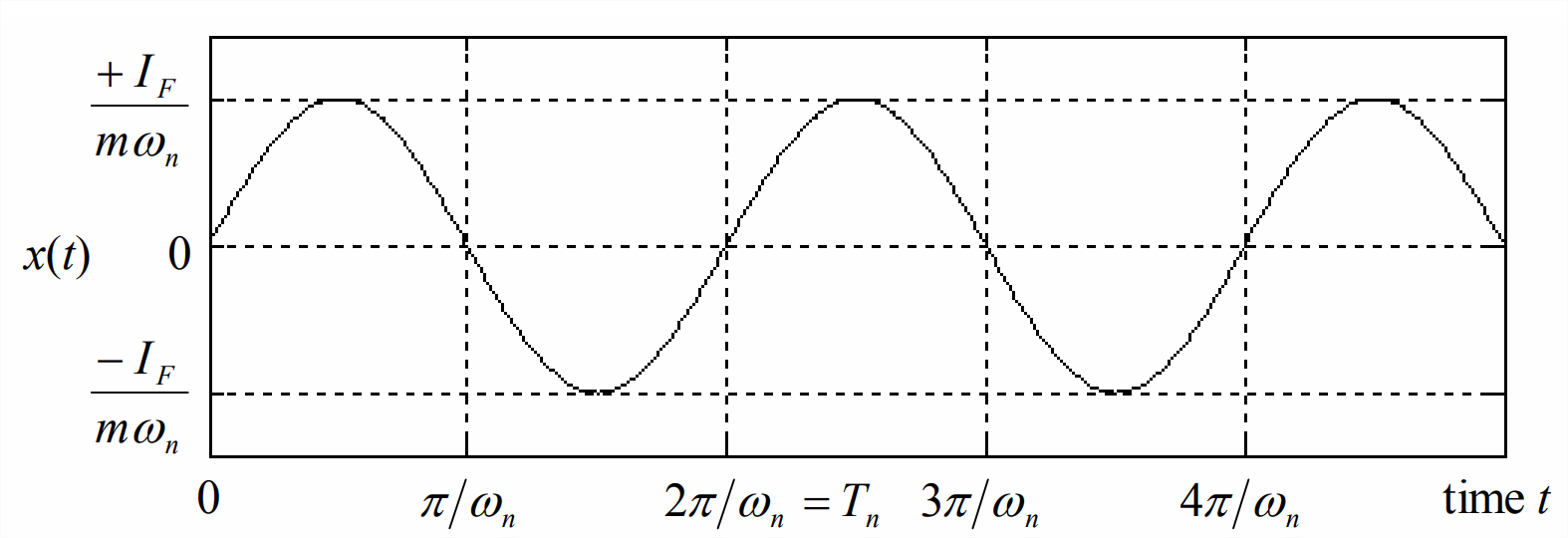
Entonces, para el movimiento traslacional\(x(t)\) de la masa, Ecuación\(\ref{eqn:8.26}\) con cero condiciones iniciales se convierte en (recordar\(k=m \omega_{n}^{2}\))

\[x(t)=\omega_{n} \frac{I_{F}}{k} \sin \omega_{n} t=\frac{I_{F}}{m \omega_{n}} \sin \omega_{n} t\label{eqn:8.28} \]

La figura\(\PageIndex{1}\) muestra algunos ciclos de ecuación de respuesta\(\ref{eqn:8.28}\).

Figura\(\PageIndex{1}\): Respuesta de impulso ideal de un sistema masa-resorte