8.11: Soluciones Numéricas Aproximadas Basadas en la Suma de Convolución

^{En la Sección 6.5, desarrollamos una fórmula de recurrencia para la solución numérica aproximada de una ODE LTI de primer orden con cualquier IC y cualquier función de entrada físicamente plausible\(u(t)\).} Es posible generalizar el enfoque de la fórmula de recurrencia a las ODEs LTI de ^segundo orden y superior, pero requeriría un desarrollo de teoría y detalle que están más allá de los objetivos de este libro (ver, para ejemplos: Craig, 1982, Sección 7.1; y Meirovitch, 2001, Sección 4.10). ^{Sin embargo, existe un enfoque alternativo relativamente simple basado en la integral de convolución, y este enfoque es fácilmente aplicable al cálculo de soluciones numéricas aproximadas para la respuesta forzada de sistemas LTI de primer y segundo orden.}

Para describir este enfoque, se inicia con la convolución general (Duhamel) integral para respuesta forzada, la cual es válida para cualquier sistema LTI:

\[\left.x(t)\right|_{I C s=0}=\int_{\tau=0}^{\tau=t} u(\tau) h(t-\tau) d \tau\label{eqn:8.41} \]

Si las condiciones iniciales (CI) no son cero, entonces se deben agregar soluciones de respuesta CI apropiadas a la integral de convolución, que representa solo la respuesta forzada. Ejemplos de tales soluciones de respuesta CI se dan explícitamente en las ecuaciones (6-5), (7-9) y, posteriormente, (9-20). En adelante en esta sección, consideraremos únicamente la respuesta forzada, por lo que será conveniente omitir el subíndice “\(IC\)s = 0” de la variable de salida y denotarlo simplemente como\(x(t)\), y posteriormente como\(x\) con los subíndices,\(x_5\) por ejemplo.

Buscamos evaluaciones aproximadas de Ecuación\(\ref{eqn:8.41}\) en forma de series temporales, es decir, en instantes discretos e igualmente espaciados en el tiempo. En consecuencia, al igual que en la Sección 6.5, definimos la siguiente notación que emplea subíndices descriptivos, con el instante inicial definido como tiempo cero:

\(t=\)	\(t_1=0\)	\(t_2=t_1 + \Delta t = \Delta t\)	\(t_3=t_2 + \Delta t = 2 \Delta t\)	\(\dots\)	\ (\ begin {array} {c} t_ {n} =t_ {n-1} +\ Delta t\\ =( n-1)\ Delta t \ end {array}\)	\(\dots\)
\(x(t)=\)	\(x_{1}\)	\(x_{2}\)	\(x_{3}\)	\(\dots\)	\(x_n\)	\(\dots\)
\(u(t)=\)	\(u_{1}\)	\(u_{2}\)	\(u_{3}\)	\(\dots\)	\(u_n\)	\(\dots\)
\(h(t)=\)	\(h_{1}\)	\(h_{2}\)	\(h_{3}\)	\(\dots\)	\(h_n\)	\(\dots\)

Designemos como secuencia de longitud\(N\) cualquier serie de\(N\) números como\(t_{1}, t_{2}, \ldots, t_{N}\), o\(x_{1}, x_{2}, \ldots, x_{N}\) y denotemos toda la secuencia como\(\{t\}_{N}\), o\(\{x\}_{N}\). Si el tiempo\(t\) es la variable independiente, y cuantificar\(f(t)\) es cualquier función dependiente del tiempo, denotemos los valores de\(f(t)\) a veces\(t_{1}, t_{2}, \ldots, t_{N}\) como\(\{f(t)\}_{N}\).

Solución de respuesta forzada La ecuación\(\ref{eqn:8.41}\) es exacta. Pero ahora introducimos lo que, en general, es una aproximación. Suponemos que el producto integrand\(u(\tau) h(t-\tau)\) varía tan poco a lo largo del paso de tiempo de integración\(\Delta t\) que introduce solo un pequeño error para aproximarse\(u(\tau) h(t-\tau)\) como constante sobre\(\Delta t\), permaneciendo su valor que al inicio del paso de tiempo:

\[u(\tau) h(t-\tau) \approx u\left(t_{k-1}\right) h\left(t-t_{k-1}\right) \text { for } t_{k-1} \leq \tau<t_{k}\label{eqn:8.42} \]

En Ecuación\(\ref{eqn:8.42}\),\(k\) es un índice que varía, así como\(\tau\) varía sobre los límites de integración en Ecuación\(\ref{eqn:8.41}\).

Supongamos que tenemos secuencias coincidentes de tiempo\(\{t\}_{N}\)\(\{u(t)\}_{N}\), entrada e IRF\(\{h(t)\}_{N}\), y deseamos calcular la secuencia de salida de respuesta forzada correspondiente,\(\{x(t)\}_{N}\). Luego, usando la ecuación de aproximación\(\ref{eqn:8.42}\), expresamos la ecuación de la\(\ref{eqn:8.41}\) siguiente manera, con la integral de convolución aproximada como una suma:

\ [\ izquierda. \ begin {array} {l}
x\ left (t_ {1}\ right) =0\\
x\ left (t_ {n}\ right) =\ sum_ {k=1} ^ {n-1} u\ left (t_ {k}\ right) h\ left (t_ {n} -t_ {k}\ right)\ delta t,\ text {for} 2\ leq\ n leq N
\ end {array}\ derecho\}\ etiqueta {eqn:8.43}\]

Una explicación adicional de la Ecuación\(\ref{eqn:8.43}\) podría ser útil, ya que la extrapolación\(\ref{eqn:8.41}\) de la Ecuación del tiempo continuo al tiempo discreto no es completamente obvia. Físicamente, la respuesta forzada debe ser cero en el instante\(t=t_{1}=0\) en que se inicia el forzamiento, aunque el valor de entrada inicial\(u(0)\) sea distinto de cero; también, la ecuación integral de convolución exacta\(\ref{eqn:8.41}\) da el mismo resultado para el límite superior\(\tau=t_{1}=0\); de ahí,\(x\left(t_{1}\right)=0\). En cuanto a la suma solo sobre\(n − 1\) los valores\(u\left(t_{k}\right) h\left(t_{n}-t_{k}\right) \Delta t\) de producto para obtener\(x\left(t_{n}\right)\), considere nuevamente la ecuación de aproximación\(\ref{eqn:8.42}\). Ecuación\(\ref{eqn:8.42}\) significa que el último término en la suma de la Ecuación\(\ref{eqn:8.43}\) que se aproxima a la integral para\(x\left(t_{n}\right)\) es el producto\(u\left(t_{n-1}\right) h\left(t_{n}-t_{n-1}\right) \Delta t\).

La ecuación se\(\ref{eqn:8.43}\) puede escribir en la siguiente forma más simple, usando notación de subíndice y la constancia del paso de tiempo\(\Delta t\):

\ [\ izquierda. \ begin {array} {l}
x_ {1} =0\\
x_ {n} =\ Delta t\ suma_ {k=1} ^ {n-1} u_ {k} h_ {n-k},\ texto {para} 2\ leq n\ leq N
\ fin {array}\ derecho\}\ etiqueta {eqn:8.44}\]

La suma en Ecuación\(\ref{eqn:8.44}\) se llama suma de convolución.

Es instructivo escribir explícitamente algunos términos de Ecuación\(\ref{eqn:8.44}\), y luego estudiar una interpretación gráfica del proceso. Supongamos que tenemos secuencias de valores de entrada\(\{u(t)\}_{N}\) y valores IRF\(\{h(t)\}_{N}\)\(N \geq 4\), con longitud, y deseamos encontrar la secuencia de respuestas correspondiente\(\{x(t)\}_{N}\). Entonces los primeros cinco términos en la secuencia de respuesta, de Ecuación\(\ref{eqn:8.44}\), son:

\[x_{1}=0\label{eqn:8.45a} \]

\[x_{2}=\Delta t\left(u_{1} h_{1}\right)\label{eqn:8.45b} \]

\[x_{3}=\Delta t\left(u_{1} h_{2}+u_{2} h_{1}\right)\label{eqn:8.45c} \]

\[x_{4}=\Delta t\left(u_{1} h_{3}+u_{2} h_{2}+u_{3} h_{1}\right)\label{eqn:8.45d} \]

\[x_{5}=\Delta t\left(u_{1} h_{4}+u_{2} h_{3}+u_{3} h_{2}+u_{4} h_{1}\right)\label{eqn:8.45e} \]

La figura\(\PageIndex{1}\) de la siguiente página es una representación gráfica de muchos aspectos de la discusión anterior. La figura consta de tres gráficas de funciones conceptuales dependientes del tiempo, con los tres ejes de tiempo alineados. La gráfica superior es una función de entrada típica,\(u(t)\) y una gráfica en la gráfica media es una función de respuesta unidad-impulso (IRF)\(h(t)\), que se eligió para parecerse al IRF exponencial de un sistema ^de primer orden, con, en particular,\(h(0) \neq 0\). La segunda gráfica (discontinua) en la gráfica media es la función\(h\left(t_{4}-t\right)\), y se eligió para ilustrar la ecuación\(\ref{eqn:8.45e}\) para la cantidad de salida\(x_5\).

Observe en la gráfica media de la Figura\(\PageIndex{1}\) que\(h\left(t_{4}-t\right)\) se deriva de\(h(t)\) “plegando”\(h(t)\) alrededor de una línea vertical a través del tiempo\(t_{4} / 2\) y luego estableciendo a cero la función plegada para todos los tiempos\(t<0\). Una de las definiciones del diccionario para la palabra “convolución” como sustantivo es “un pliegue”, y esta es aparentemente la razón del uso de “convolución” como nombre de una transformada, integral o suma (Evans, 1954, pp. 199-204). Parece que “suma de convolución”, por ejemplo, suena más elegante en inglés que “suma plegable”; sin embargo, el sustantivo alemán para convolución matemática es Faltung, que significa “plegar” o “doblar”, y Faltung a menudo se usaba indistintamente con “convolución” en el idioma inglés más antiguo libros de texto y otra literatura técnica.

Figura\(\PageIndex{1}\): Representación gráfica de la suma de convolución para un problema conceptual con función de entrada\(u(t)\) y función impulso-respuesta\(h(t)\), con\(h(0) \neq 0\).

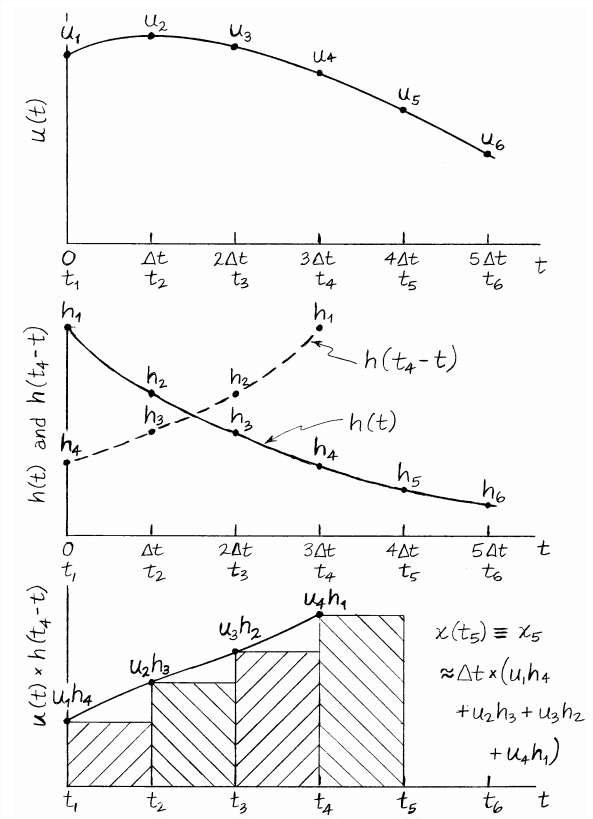
La gráfica en la gráfica inferior de la Figura\(\PageIndex{1}\) es el producto\(u(t) h\left(t_{4}-t\right)\). En los tiempos\(t_{1}\),\(t_{2}\),\(t_{3}\), y\(t_{4}\), los productos discretos\(u_{k} h_{5-k}\) están marcados, y la ecuación\(\ref{eqn:8.42}\) de aproximación de constancia por partes se ilustra mediante líneas horizontales rectas, cada una representando el paso de tiempo\(\Delta t\). Se trata de una aproximación escalinata similar a la utilizada en la Sección 6.5. El gráfico inferior muestra que Ecuación\(\ref{eqn:8.45e}\) para\(x_5\) es el área bajo todos los rectángulos rayados (toda la “escalera”); esa área es una aproximación de la integral de la Ecuación\(\ref{eqn:8.41}\),\(\int_{\tau=0}^{\tau=t_{5}} u(\tau) h\left(t_{5}-\tau\right) d \tau\). Es obvio a partir de esta interpretación gráfica de la suma de convolución que valores menores de paso de tiempo\(\Delta t\) producirán integraciones numéricas más precisas, a expensas de cálculos más largos.

Para el ejemplo conceptual de Figura\(\PageIndex{1}\), que se asemeja a un sistema ^de primer orden que tiene valor IRF inicial\(h(0)=h_{1} \neq 0\), y también valor de entrada inicial\(u(0)=u_{1} \neq 0\), Ecuación\(\ref{eqn:8.45b}\) da\(x_{2}=\Delta t\left(u_{1} h_{1}\right) \neq 0\). Esto se nota porque es fácil cometer el error de calcular tiempo aproximado de respuesta aplicando directamente la función MATLAB conv, como en la línea de comandos X = conv (u, h), y luego tomando los primeros\(N\) elementos de la secuencia resultante\(\{X\}_{2 N-1}\) para que sean los deseados respuesta forzada,\(\{x(t)\}_{N}\); este proceso ejecuta la ecuación incorrecta

\[x\left(t_{n}\right)=\sum_{k=1}^{n} u\left(t_{k}\right) h\left(t_{n+1}-t_{k}\right) \Delta t=x_{n}=\Delta t \sum_{k=1}^{n} u_{k} h_{n+1-k} \nonumber \]

para\(1 \leq n \leq N\).

Esta ecuación incorrecta calcula una secuencia con\(N-1\) elementos iguales a los de la secuencia de respuesta forzada correcta, pero la secuencia incorrecta se desplaza hacia atrás en el tiempo por un solo paso de tiempo,\(\Delta t\). En particular, los conjuntos de procesos incorrectos\(x_{1}=\Delta t\left(u_{1} h_{1}\right)\), que serían distintos de cero para el problema conceptual de la Figura\(\PageIndex{1}\), y podrían alertar al analista de que algo anda mal. (Recordemos de la discusión anterior que el valor inicial de respuesta forzada\(x_1\) debe ser cero.) ^{Pero para la mayoría de los sistemas que no sean los sistemas estándar de primer orden, el valor inicial del IRF es cero\(h_{1}=0\), por lo que el error en no\(x_{1}=\Delta t\left(u_{1} h_{1}\right)\) sería obvio en los resultados calculados.} Las lecciones de esta discusión son:

1. el uso de la suma de convolución incorrecta podría producir resultados que no son obviamente incorrectos; de hecho, para muy pequeños\(\Delta t\), las parcelas incorrectas y correctas de respuesta aproximada versus tiempo podrían ser casi indistinguibles visualmente; y
2. si aplica directamente la función conv de MATLAB, entonces, para obtener la secuencia de respuesta forzada aproximada correcta, asegúrese de desplazar la secuencia calculada por conv hacia adelante en el tiempo en un solo paso de tiempo\(\Delta t\),, y establecer\(x_{1}=0\).

A continuación se presentan dos ejemplos numéricos de la aplicación de la Ecuación\(\ref{eqn:8.44}\), primero para una ^ODE de primer orden, siguiente para una ODE de ^segundo orden sin amortiguar.

Ejemplo de convolución-suma\(\PageIndex{1}\): 1^st order systems

^{Considere el LTI-ODE estándar de primer orden de un sistema estable, Ecuación 3.4.8, para la variable dependiente\(x(t)\):\(\dot{x}+\left(1 / \tau_{1}\right) x=b u(t)\).} De la Sección 8.5 y tarea Problema 8.5.1, la función unidad-impulso-respuesta (IRF) es\(h(t)=b e^{-t / \tau_{1}}\). Letus establece la función de entrada para ser una rampa decreciente\(u(t)= c(a-t)\),, en la que\(c\), una constante dimensional, es la pendiente descendente de la rampa, y\(a\) es el tiempo en el que la entrada pasa por cero. Como referencia, la solución exacta para este problema se deriva de las Ecuaciones 6.2.4 o\(\ref{eqn:8.41}\) ¹:

\[x(t)=b e^{-t / \tau_{1}} \int_{\tau=0}^{\tau=t} e^{\tau / \tau_{1}} u(\tau) d \tau=b e^{-t / \tau_{1}} \int_{\tau=0}^{\tau=t} e^{\tau / \tau_{1}} c(a-\tau) d \tau \nonumber \]

\[=b c \tau_{1}\left[\left(a+\tau_{1}\right)\left(1-e^{-t / \tau_{1}}\right)-t\right] \nonumber \]

Con parámetros\(\tau_{1}\) = 2.5 s,\(a\) = 10 s,\(b\) = 3.5 y\(c\) = 1 (b y c en unidades consistentes), los comandos de MATLAB para calcular y trazar la solución exacta\(x(t)\), y la solución aproximada de la ecuación\(\ref{eqn:8.44}\), para el paso de tiempo relativamente grande\(\Delta t\) = 1 s, son dado a continuación, seguido de la gráfica resultante, la cual fue editada posteriormente para agregar etiquetas, título y leyenda. Observe en el código MATLAB que la rampa decreciente se introduce en la secuencia de entrada\(\{u(t)\}_{N}\), al igual que la secuencia IRF\(\{h(t)\}_{N}\). Tenga en cuenta que el código simple para calcular las sumas de convolución en toda la secuencia de respuesta forzada,\(\frac{x_{n}}{\Delta t}=\sum_{k=1}^{n-1} u_{k} h_{n-k}\) for\(2 \leq n \leq N\), consiste en un bucle for sobre índice\(k\) anidado dentro de un bucle for sobre índice\(n\).

>> a=10; b=3.5; c=1; tau=2.5;

dt=1; t=0:dt:10;

N=longitud (t);% longitud de secuencia

u=c* (a*ones (1, N) -t);% de excitación de rampa decreciente

plot (t, tau*b*u, 'k—'), rejilla %respuesta pseudo-estática

h=b*exp (-t/tau); %IRF, función impulso-respuesta

xc (1) =0; %cero valor inicial

para n=2:N

suma=0;

para k=1 :( n-1)

suma=suma+u (k) *h (n-k);

final

xc (n) =suma;

final

xc=dt*xc;

bodega, parcela (t, xc, 'ko-')

te= 0:0. 05:10;

xe=c*b*tau* ((a+tau) * (1-exp (-te/tau)) -te); %solución exacta

parcela (te, xe, 'k')

Figura\(\PageIndex{1}\)

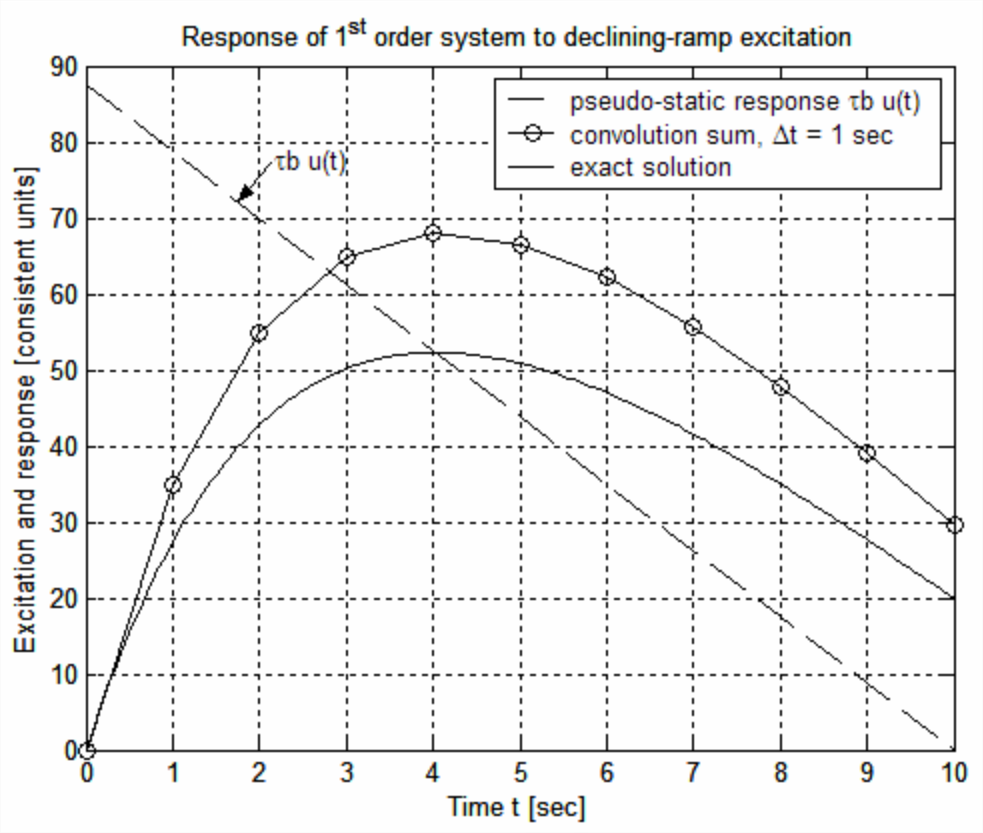
La gráfica anterior muestra que la ecuación\(\ref{eqn:8.44}\) con el paso de tiempo relativamente grande\(\Delta t=1\) s produce una mala aproximación a la solución exacta de la ODE ^de primer orden en este problema. Las siguientes líneas de comandos de MATLAB evalúan Ecuación\(\ref{eqn:8.44}\) y trazan los resultados para tres valores progresivamente más pequeños de\(\Delta t\).

>> a=10; b=3.5; c=1; tau=2.5;

tend=10;

m= [2 8 16];% inversos de pasos de tiempo para convolución

maxln=tend*max (m) +1;

t=ceros (3, maxln); xc=ceros (3, maxln); %inicializar matrices sobredimensionadas

para j= 1:3

dt=1/m (j); tj=0:dt:tender; N (j) =longitud (tj); t (J,1:n (j)) =tj;

u=c* (a*unos (1, N (j)) - tj); %excitación

h=b*exp (-tj/tau); %IRF

xc (j,1) =0; %cero valor inicial

para n=2:N (j)

suma=0;

para k=1 :( n-1)

suma=suma+u (k) *h (n-k);

final

xc (j, n) =dt*suma;

final

final

parcela (t (1,1:N (1)), xc (1,1:N (1)), 'ko', t (2,1:N (2)), xc (2,1:N (2)), 'ks')

mantener, parcela (t (3,1:N (3)), xc (3,1:N (3)), 'k.')

te= 0:0 .05:tender;

xe=c*b*tau* ((a+tau) * (1-exp (-te/tau)) -te); %solución exacta

parcela (te, xe, 'k'), rejilla

Figura\(\PageIndex{2}\)

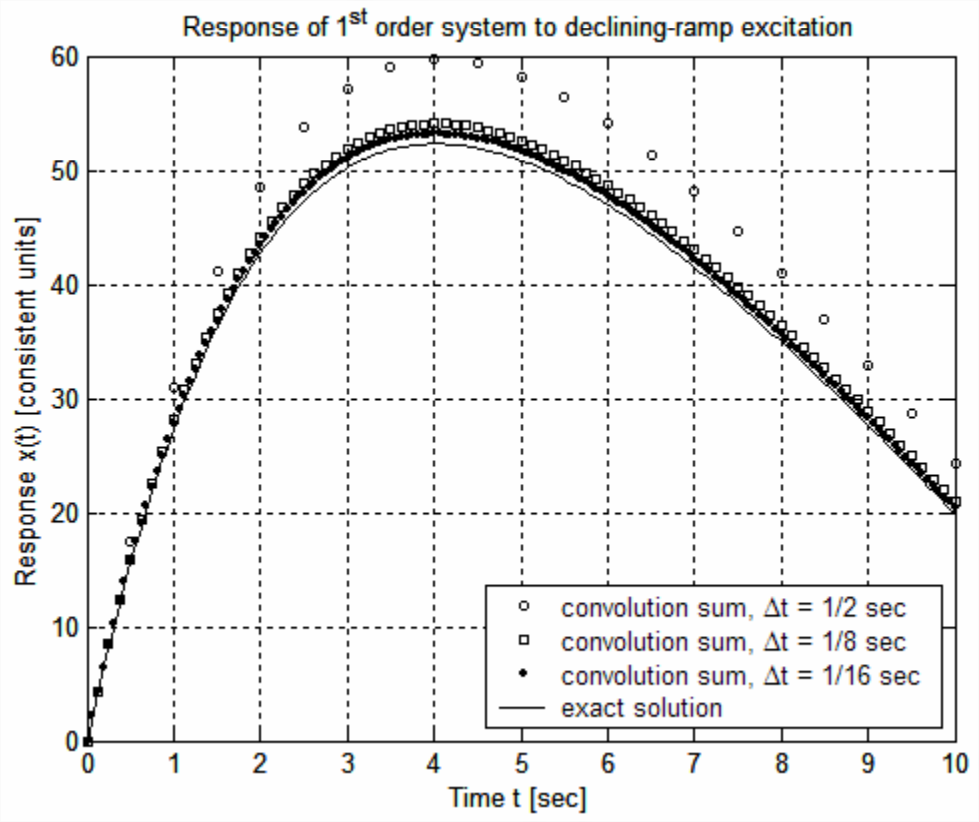
Los resultados anteriores demuestran para este sistema de primer ^orden que la solución aproximada calculada a partir de la suma de convolución se aproxima a la solución exacta como\(\Delta t \rightarrow 0\). Esto concluye Convolución-suma Ejemplo 1.

Ejemplo de convolución-suma\(\PageIndex{2}\): undamped 2^nd order system

Considere la Ecuación LTI-ODE 7.1.5 para un sistema estándar de ^segundo orden no amortiguado\(\ddot{x}+\omega_{n}^{2} x=\omega_{n}^{2} u(t)\),, con CI\(x(0)=0\) y\(\dot{x}(0)=0\). De las Secciones 8.7 y 8.10 [Ecuaciones 8.7.3 y 8.10.2], la función unidad-impulso-respuesta (IRF) es\(h(t)=\omega_{n} \sin \omega_{n} t\). Vamos a establecer la función de entrada para que sea un pulso de rampa decreciente,

\ [u (t) =\ left\ {\ begin {array} {c}
c (a-t), 0\ leq t<t_ {d}\\
0, t_ {d} <t
\ end {array}\ derecha. \ nonumber\]

en la que\(c\), una constante dimensional, es la pendiente descendente de la rampa,\(ca\) es la entrada a\(t = 0\), y\(t_d\) es la duración del pulso. Como referencia, las ecuaciones de solución exacta para este problema se derivan a continuación de las Ecuaciones 7.2.4 y 7.2.5, sin detalles de los procesos de integración. Para el intervalo durante el cual el pulso está activo,\(0 \leq t \leq t_{d}\), aplicamos la Ecuación 7.2.4, aunque la Ecuación 7.2.5 serviría igual de bien:

\[x(t)=\omega_{n} \int_{\tau=0}^{\tau=t} \sin \omega_{n} \tau \times u(t-\tau) d \tau=\omega_{n} \int_{\tau=0}^{\tau=t} \sin \omega_{n} \tau \times c[a-(t-\tau)] d \tau \nonumber \]

\[=c\left[a-t-a \cos \omega_{n} t+\left(1 / \omega_{n}\right) \sin \omega_{n} t\right], \text { valid for } 0 \leq t \leq t_{d} \nonumber \]

Para el tiempo posterior al cese del pulso,\(t_{d}<t\), la Ecuación 7.2.5 es preferible ya que la entrada\(u(t)\) es cero para\(t_{d}<t\), de manera que el límite superior de integración es claramente\(t_{d}\):

\[x(t)=\omega_{n} \int_{\tau=0}^{\tau=t} \sin \omega_{n}(t-\tau) \times u(\tau) d \tau=\omega_{n} \int_{\tau=0}^{\tau=t_{d}} \sin \omega_{n}(t-\tau) \times c(a-\tau) d \tau \nonumber \]

\[=\omega_{n} c\left[\sin \omega_{n} t \int_{\tau=0}^{\tau=t_{d}} \cos \omega_{n} \tau \times(a-\tau) d \tau-\cos \omega_{n} t \int_{\tau=0}^{\tau=t_{d}} \sin \omega_{n} \tau \times(a-\tau) d \tau\right] \nonumber \]

\ [\ izquierda. \ begin {array} {l}
=c\ izquierda\ {\ sin\ omega_ {n} t\ izquierda [a\ sin\ omega_ {n} t_ {d} -\ izquierda (1/\ omega_ {n}\ derecha)\ izquierda (\ omega_ {n} t_ {d}\ sin\ omega_ {n} t_ {d} +\ cos\ omega_ {n} t_ {d} -1\ derecha)\ derecha]\ derecha. \\
. \ end {array}\ right\},\ text {válido para} t_ {d} <t\ nonumber\]

Que los parámetros sean: frecuencia natural no amortiguada\(\omega_{n}=\pi / 4.5\) rad/s (haciendo el periodo asociado 9 s),\(2\) = 10 s,\(c\) = 1 (en unidades consistentes), y periodo de pulso\(t_d\) = 10 s ². Los comandos de MATLAB para calcular y trazar la solución exacta\(x(t)\), y la solución aproximada de Ecuación\(\ref{eqn:8.44}\), para el paso de tiempo relativamente grande\(\Delta t\) = 1 s, se dan a continuación, seguido del gráfico resultante de respuesta, que se editó más tarde para agregar etiquetas, título y leyenda. Observe en el código MATLAB que todo el pulso de rampa decreciente, incluidos los ceros, se ingresa en la secuencia de entrada\(\{u(t)\}_{N}\), al igual que la secuencia IRF\(\{h(t)\}_{N}\). Además, al igual que en el Ejemplo 1 de convolución-suma, el código simple para calcular las sumas de convolución en toda la secuencia de respuesta forzada,\(\frac{x_{n}}{\Delta t}=\sum_{k=1}^{n-1} u_{k} h_{n-k}\) for\(2 \leq n \leq N\), consiste en un bucle for sobre índice\(k\) anidado dentro de un bucle for sobre índice\(n\).

>> a=10; c=1; wn=pi/4.5; td=10;

tend=25; %intervalo de tiempo (seg)

dt=1; t=0:dt:tender;

nd=td/dt+1; %warning: no necesariamente un entero para td arbitrario

N=longitud (t);% longitud de secuencia

u=ceros (1, N);

u (1:nd) =c* (a*ones (1, nd) -t (1:nd));% de pulso de rampa decreciente

plot (t (1:nd), u (1:nd), 'k—'), rejilla %respuesta pseudo-estática

hold, plot (t (Nd:n), ceros (1, (N-nd+1)), 'k—')

h=wn*sin (wn*t); %IRF, función impulso-respuesta

xc (1) =0; %cero valor inicial

para n=2:N

suma=0;

para k=1 :( n-1)

suma=suma+u (k) *h (n-k);

final

xc (n) =suma;

final

xc=dt*xc;

parcela (t, xc, 'ko-')

t1= 0:0 .1:td; t2 =( td+0.1) :0.1:tender; te= [t1 t2];

wt1=wn*t1; wt2=wn*t2;

x1 = c* (a-t1-a*cos (wt1) +sin (wt1) /wn);

arg=wn*td; sn=sin (arg); cn=cos (arg);

s=a*sn- (arg*sn+cn-1) /wn; C=a* (1-cn) - (-arg*cn+sn) /wn;

x2 = c* (S*sin (wt2) -c*cos (wt2));

xe= [x1 x2]; %solución exacta

parcela (te, xe, 'k')

Figura\(\PageIndex{3}\)

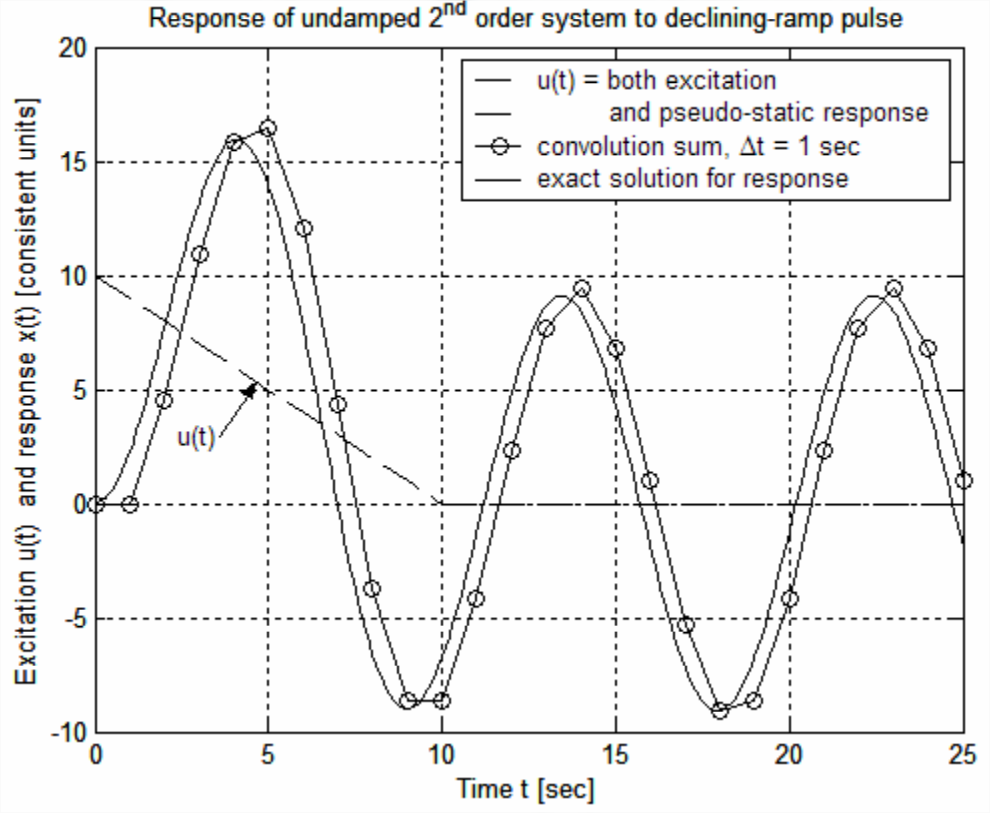
El gráfico anterior muestra que la ecuación\(\ref{eqn:8.44}\) con el paso de tiempo relativamente grande\(\Delta t\) = 1 s produce solo una aproximación mediocre a la solución exacta de la ODE ^{de segundo} orden en este problema. Pero la gráfica de la solución convolución-suma también ilustra un punto importante: no solo es\(x_1\) = 0, el requisito discutido anteriormente, sino también\(x_2\) =\(u_1h_1\) = 0 porque el valor inicial de IRF\(h_1\) = 0 para la ODE de ^segundo orden, independientemente del valor inicial\(u_1\) de la entrada. La aproximación apropiada en este caso para la derivada de tiempo inicial de respuesta es\(\frac{d x}{d t}(t=0) \approx \frac{x_{2}-x_{1}}{\Delta t}=0\). Las condiciones iniciales necesarias (CI) para una ODE ^{de segundo} orden son ambas\(x(0)\) y\(\dot{x}(0)\). Como se afirma al inicio de esta sección, cualquier CI distinto de cero debe ser contabilizado por soluciones de respuesta CI separadas, ya que estos CI no pueden incluirse en la solución de respuesta forzada, que es la suma de convolución. Esto significa que debemos tener\(x_{1}=x_{2}=0\) para esto, o, de hecho, cualquier solución aproximada de convolución-suma correcta de una ODE estándar de 2 ^nd orden. La gráfica anterior de la solución convolución-suma también demuestra una consecuencia negativa (relativa a la precisión numérica) de la condición necesaria\(x_{2}=0\): un lapso de tiempo consistente, de la solución aproximada relativa a la solución exacta, del orden de\(\Delta t\). Las siguientes líneas de comandos de MATLAB evalúan Ecuación\(\ref{eqn:8.44}\) y trazan los resultados (en la página siguiente) para dos valores progresivamente más pequeños de\(\Delta t\).

>> a=10; c=1; wn=pi/4.5; td=10;

tend=25; %intervalo de tiempo (seg)

m= [2 8]; %inversos de pasos de tiempo para convolución

maxln=tend*max (m) +1;

t=ceros (2, maxln); xc=ceros (2, maxln); %inicializar matrices sobredimensionadas

para j= 1:2

dt=1/m (j); tj=0:dt:tender; N (j) =longitud (tj); t (J,1:n (j)) =tj;

nd=td/dt+1; %warning: no es un entero para td arbitrario

u=ceros (1, N (j));

u (1:nd) =c* (a*ones (1, nd) -tj (1:nd));% pulso de rampa decreciente

h=wn*sin (wn*tj); %IRF, función impulso-respuesta

xc (j,1) =0; %cero valor inicial

para n=2:N (j)

suma=0;

para k=1 :( n-1)

suma=suma+u (k) *h (n-k);

final

xc (j, n) =dt*suma;

final

final

parcela (t (1,1:N (1)), xc (1,1:N (1)), 'ks')

mantener, parcela (t (2,1:N (2)), xc (2,1:N (2)), 'k.') , rejilla

t1= 0:0 .1:td; t2 =( td+0.1) :0.1:tender; te= [t1 t2];

wt1=wn*t1; wt2=wn*t2;

x1 = c* (a-t1-a*cos (wt1) +sin (wt1) /wn);

arg=wn*td; sn=sin (arg); cn=cos (arg);

s=a*sn- (arg*sn+cn-1) /wn; C=a* (1-cn) - (-arg*cn+sn) /wn;

x2 = c* (S*sin (wt2) -c*cos (wt2));

xe= [x1 x2]; %solución exacta

parcela (te, xe, 'k')

Figura\(\PageIndex{4}\)

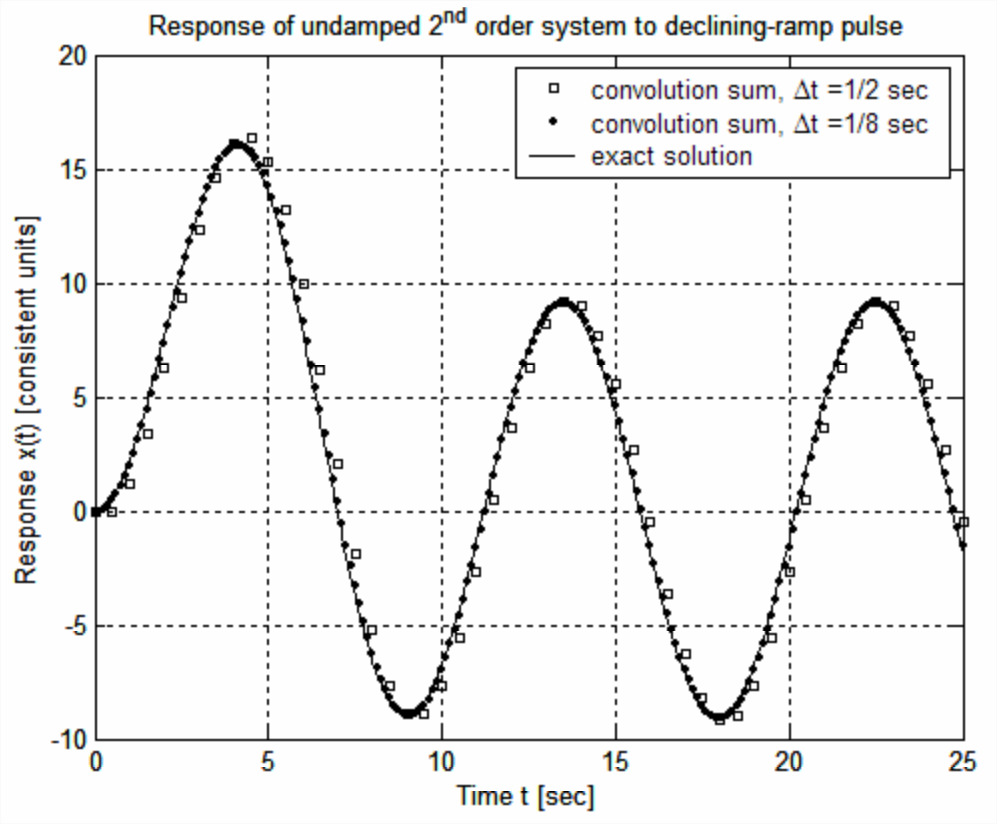
La solución numérica para el paso de tiempo\(\Delta t=1 / 2\) s es una solución aproximada justa, pero aún con un retraso de tiempo notable, relativo a la solución exacta, del orden de\(\Delta t\). Sin embargo, la solución numérica para el paso de tiempo\(\Delta t=1 / 8\) s es casi indistinguible de la solución exacta a simple vista en la gráfica. Esto concluye Convolución-suma Ejemplo 2.

Finalmente, observamos una curiosa intersección de dos operaciones matemáticas aparentemente no relacionadas, suma de convolución y multiplicación de polinomios. Supongamos que tenemos dos secuencias arbitrarias de números,\(\{u\}_{N}\) y\(\{h\}_{M}\). Considere la suma de convolución en la forma aplicada por la línea de comandos de MATLAB X = conv (u, h), que produce la secuencia\(X_{n}=\sum_{k=1}^{n} u_{k} h_{n+1-k}\) para\(1 \leq n \leq(N+M-1): \quad X_{1}=u_{1} h_{1}, \quad X_{2}=u_{1} h_{2}+u_{2} h_{1}, \quad X_{3}=u_{1} h_{3}+u_{2} h_{2}+u_{3} h_{1}, \quad X_{4}=u_{1} h_{4}+u_{2} h_{3}+u_{3} h_{2}+u_{4} h_{1}\), etc. Evans (1954, pp. 201-203) observó que el proceso de convolución-suma se puede ejecutar con el uso de tablas en un “proceso similar a multiplicación”. Primero, definimos la tabla de secuencias\(\{h\}_{M}\) y\(\{u\}_{N}\):

\(\{h\}_{M}=\)	\(h_1\)	\(h_2\)	\(h_3\)	\(h_4\)	\(\dots\)
\(\{u\}_{N}=\)	\(u_1\)	\(u_2\)	\(u_3\)	\(u_4\)	\(\dots\)

Con el fin de ejecutar la operación\(X_{n}=\sum_{k=1}^{n} u_{k} h_{n+1-k}\) usando las secuencias\(\{h\}_{M}\) y\(\{u\}_{N}\), construimos la tabla de productos a continuación. La primera fila de la tabla consiste en los productos\(u_{1} \times\{h\}_{M}\), la segunda fila consiste en los productos\(u_{2} \times\{h\}_{M}\) y esta secuencia está desplazada por una columna hacia la derecha, la tercera fila consiste en los productos\(u_{3} \times\{h\}_{M}\) y esta secuencia está desplazada por dos columnas hacia la derecha, etc.

	\(n=1\)	\(n=2\)	\(n=3\)	\(n=4\)	\(\dots\)
\(k=1\)	\(u_1h_1\)	\(u_1h_2\)	\(u_1h_3\)	\(u_1h_4\)	\(\dots\)
\(k=2\)		\(u_2h_1\)	\(u_2h_2\)	\(u_2h_3\)	\(\dots\)
\(k=3\)			\(u_3h_1\)	\(u_3h_2\)	\(\dots\)
\(k=4\)				\(u_4h_1\)	\(\dots\)
\(\dots\)					\(\dots\)

Entonces cada elemento\(X_{n}\) de la secuencia\(\{X\}_{N+M-1}\) es la suma de los productos en la\(n\) ^columna correspondiente de la tabla de productos anterior:

\(\{X\}_{N+M-1}=\)

\(X_{1}=u_{1} h_{1}\)

\ (\ begin {array} {l} X_ {2} =u_ {1} h_ {2} +\\ u_ {2} h_ {1} \ end {array}\)

\ (\ begin {array} {l} X_ {3} =u_ {1} h_ {3} +\\ u_ {2} h_ {2} +u_ {3} h_ {1} \ end {array}\)

\ (\ begin {array} {l} X_ {4} =u_ {1} h_ {4} +\\ u_ {2} h_ {3} +u_ {3} h_ {2} +\\ u_ {4} h_ {1} \ end {array}\)

\(dots\)

En la Sección 6.1 se dio un ejemplo numérico aplicando la función conv de MATLAB a la multiplicación de dos polinomios. Aquí hay otro ejemplo del proceso usando la notación en las tablas anteriores, el producto de un polinomio de ^1º grado,\(P_{1}\), con un polinomio de ^2º grado,\(P_{2}\):

\[P_{1} \times P_{2}=\left(u_{1} s+u_{2}\right) \times\left(h_{1} s^{2}+h_{2} s+h_{3}\right)=u_{1} h_{1} s^{3}+\left(u_{1} h_{2}+u_{2} h_{1}\right) s^{2}+\left(u_{1} h_{3}+u_{2} h_{2}\right) s+u_{2} h_{3} \nonumber \]

Con cero coeficientes polinomiales de entrada\(u_{i}=0\) para\(i > 2\) y\(h_j = 0\) para\(j > 3\), los coeficientes del polinomio cúbico producto (en orden descendente de potencias de\(s\)) son los coeficientes\(X_1\),\(X_2\),\(X_3\), y\(X_4\) de la última tabla anterior.

Si deseara ejecutar producto\(P_{1} \times P_{2}\), probablemente usaría el álgebra básica a continuación para la multiplicación de dos polinomios, que, aunque menos general, es esencialmente el mismo que el proceso tabular descrito anteriormente.

Polinomio\(P_2\) =	\(h_{1} s^{2}+\)	\(h_{2} s+\)	\(h_{3}\)
Polinomio\(P_{1}\) =	\(u_{1} s+\)	\(u_{2}\)
\(u_{1} s \times P_{2}\)=	\(u_{1} h_{1} s^{3}+\)	\(u_{1} h_{2} s^{2}+\)	\(u_{1} h_{3} s\)
\(u_{2} \times P_{2}\)(desplazamiento) =		\(u_{2} h_{1} s^{2}+\)	\(u_{2} h_{2} s+\)	\(u_{2} h_{3}\)
\(P_{1} \times P_{2}\)= sumas de columna =	\(u_{1} h_{1} s^{3}+\)	\(\left(u_{1} h_{2}+u_{2} h_{1}\right) s^{2}+\)	\(\left(u_{1} h_{3}+u_{1} h_{3}\right) s+\)	\(u_{2} h_{3}\)

¹ No se muestran los detalles del proceso de integración. Tenga en cuenta, sin embargo, que puede verificar fácilmente la validez de la solución dada sustituyéndola por la ODE y IC y encontrando que están satisfechas.

² Con\(t_d = a\), el pulso es continuo a cero cuando termina.