8.12: Capítulo 8 Tarea

1. Un pulso de fuerza “formado” de 10 milisegundos en libras se describe por la ecuación\ [\ begin {aligned}
   f_ {x} (t) =&\ left [50\ sin ^ {2} (100\ pi t)\ right]\ mathrm {lb}\\
   &\ times [H (t) -H (t-0.01\ mathrm {sec})]
   \ end {alineado}\ nonumber\] que es graficado a la derecha. En un cálculo de la respuesta del sistema a esta fuerza de entrada, deseamos aproximar la fuerza como una función de impulso ideal,\(f_{x}(t) \cong I_{F} \delta(t)\). ¿Cuál es el valor (con unidades) de\(I_{F}\)? (Pista: antes de embarcarse en una larga integración, examine la gráfica cuidadosamente en busca de simetrías que harán que el cálculo sea casi trivial).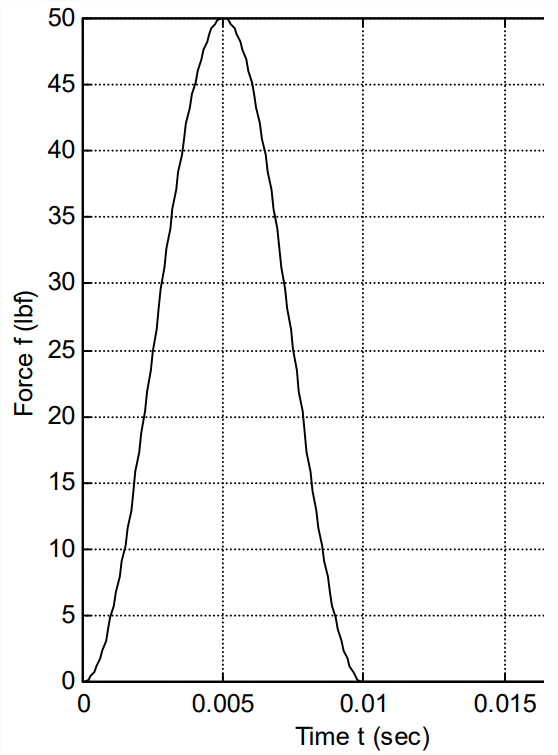

   

   Figura\(\PageIndex{1}\)

2. Considere un sistema de resorte masivo sin amortiguar. La masa pesa 20.0 lb incluyendo un propulsor de chorro de aire que está unido a ella, y el resorte se calibra para estirar 0.279 pulgadas cuando se somete a 100 lb de tensión. El propulsor de chorro de aire ha sido diseñado y calibrado para proporcionar 0.767 lb de empuje en un pulso plano casi perfecto. Estudiemos la respuesta\(x(t)\) de posición dinámica de la masa, partiendo de cero CI, a esta entrada de fuerza del propulsor.
   1. Calcular la frecuencia natural del sistema masa-resorte en rad/s y Hz, y el periodo natural del sistema en segundos y milisegundos. Calcular la magnitud de impulso\(I_{F}\) entregada por el propulsor de chorro de aire en una explosión de duración\(t_{d}\) = 4.00 milisegundos. (Respuestas parciales:\(T_{n}\) = 75.53 ms,\(I_{F}\) = 3.068 × 10-3 lb-s)
   2. Modele la explosión de chorro de aire de 4.00-ms como un pulso de fuerza plano perfecto. Para esta entrada, escriba ecuaciones que describan la respuesta real del pulso\(x(t)\) (en pulgadas); para obtener ayuda, consulte la Ecuación 8.1.6 y la Ecuación 7.1.4; no vuelva a derivar nada de lo que ya esté disponible. Utilice MATLAB para hacer una gráfica precisa del historial de tiempo de esta respuesta de pulso real\(x(t)\) (en pulgadas) a lo largo del intervalo de tiempo\(0 \leq t \leq 40\) ms.
   3. Aproximar la entrada de fuerza de chorro de aire como impulso ideal con la misma magnitud\(I_{F}\) de impulso calculada en la parte 8.2.1. Utilice la Ecuación 8.7.5 para escribir la ecuación numérica para la respuesta de impulso ideal\(x(t)\) en pulgadas.
   4. Utilice MATLAB para hacer dos gráficas de historial de tiempo precisas, en la misma gráfica, de\(x(t)\) (en pulgadas) a lo largo del lapso de tiempo\(0 \leq t \leq 40\) ms: la respuesta de pulso real de la parte 8.2.2 y la respuesta de impulso ideal de la parte 8.2.3.
3. Considera el sistema masa-resorte dibujado abajo con\(m\) = 8.03 kg y\(k\) = 317 N/m. Este sistema se encuentra inicialmente en reposo en la posición de equilibrio estático cuando es golpeado por un pulso\(f_{y}(t)=F\left[H(t)-H\left(t-t_{d}\right)\right]\) de fuerza plana de magnitud\(F=4.50\) N y corta duración\(t_d\) = 0.05 s. En este problema, analizamos el desplazamiento dinámico de la masa en relación con la posición inicial de equilibrio estático.

   

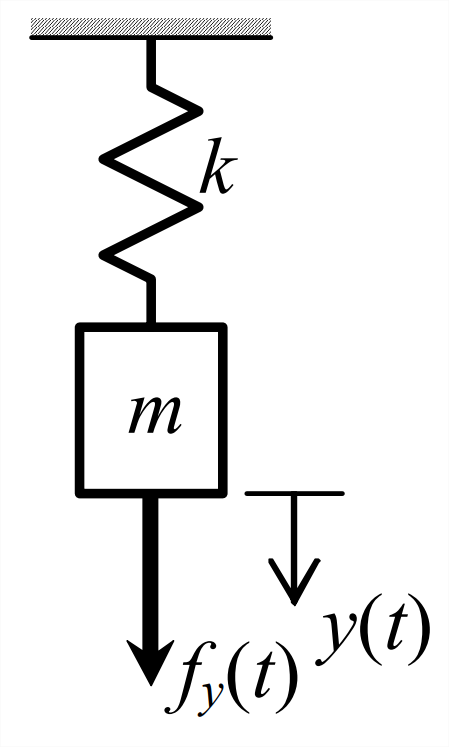
   Figura\(\PageIndex{2}\)

   1. La siguiente ecuación de respuesta sucinta se puede derivar fácilmente con el uso de la ecuación de transformada 8.1.2 y la transformada general de Laplace de una función que se traduce en el tiempo:\(L\left[f\left(t-t_{d}\right) H\left(t-t_{d}\right)\right]=e^{-s t_{d}} F(s)\). \[y(t)=\frac{F}{k}\left[\left(1-\cos \omega_{n} t\right) H(t)-\left(1-\cos \omega_{n}\left(t-t_{d}\right)\right) H\left(t-t_{d}\right)\right] \nonumber \]Mostrar que esta ecuación es totalmente equivalente a las ecuaciones de respuesta en la solución de dos partes Ecuación 8.1.6. Observe de la Ecuación 7.1.4 que\(U=F / k\).

      A continuación, utilice MATLAB para trazar la curva de respuesta\(t\) de\(y(t)\) versus de\(t\)\(t\) = 0 a = 1 s, el periodo del sistema masa-resorte.

   2. Para comparar con la respuesta real, graficar [en la misma gráfica que la parte 8.3.1] la respuesta de impulso ideal del sistema\(y(t)=\left(I_{F} / m \omega_{n}\right) \sin \omega_{n} t\), Ecuación 8.7.5, utilizando para\(I_{F}\) el valor del impulso real a partir de datos dados. Etiquete claramente qué curva es la respuesta real y cuál es la respuesta de impulso ideal; título y etiqueta tu gráfica apropiadamente.
4. En este ejercicio, apliquemos el teorema del valor inicial al problema de la Sección 8.7: el sistema estándar de ^segundo orden sin amortiguar que tiene condiciones iniciales distintas de cero y se ve perturbado por un impulso ideal,\(u(t)=I_{U} \delta(t)\).
   1. Determinar el valor inicial post-impulso,\(x\left(0^{+}\right)\), usando la Ecuación 8.7.2 para en el teorema del valor inicial. ¿Tu resultado es el mismo que el encontrado directamente de la Ecuación 8.7.3?
   2. Utilice la Ecuación 8.7.2\(L[x(t)]\) para encontrar la transformada\(L[\dot{x}(t)]\) de Laplace de la función “velocidad”; asegúrese de incluir ambos términos de la Ecuación 8.6.3 para la transformación de una derivada.
   3. Determina la “velocidad” inicial post-impulso,\(\dot{x}\left(0^{+}\right)\), usando tu\(L[\dot{x}(t)]\) de la parte 8.4.2 en el teorema del valor inicial. ¿Tu resultado es el mismo que el de la Ecuación 8.8.2?
5. ^{Considerar el LTI-ODE de primer orden estándar (de un sistema físico estable) para la variable dependiente\(x(t)\):\(\dot{x}+\left(1 / \tau_{1}\right) x=b u(t)\), con IC\(x(0)=0\), y con excitación por un impulso ideal,\(u(t)=I_{U} \delta(t)\).}
   1. Deducir de los resultados de la Sección 8.5 la función unidad-impulso-respuesta (IRF),\(h(t)\).
   2. Utilice el resultado de la parte 8.5.1 para escribir la solución de respuesta integral Duhamel para el sistema estándar de primer ^orden estable, que es comparable a la Ecuación 8.11.2 para el sistema estándar de ^segundo orden sin amortiguar.
   3. El objeto de esta parte es comparar numéricamente la respuesta de impulso ideal derivada en la Sección 8.5 con la respuesta a un pulso real plano que tiene la misma magnitud de impulso que el impulso ideal y una duración de pulso que es corta en relación con la constante de tiempo del sistema. Utilice MATLAB para hacer dos gráficas precisas del historial de tiempo, en la misma gráfica, de la salida adimensional\(x(t) / b I_{U}\) frente al tiempo adimensional\(t / \tau_{1}\) durante el intervalo de tiempo\(0 \leq t / \tau_{1}\leq 1\). Una trama será la respuesta al impulso ideal. La otra gráfica será la respuesta a un pulso plano que tenga duración adimensional\(t_{d} / \tau_{1}=0.2\); para esta gráfica, utilice las ecuaciones de respuesta derivadas en la tarea Problema 6.2. Debe encontrar que la respuesta de impulso ideal es mucho más fácil de calcular que la respuesta de pulso real. Sin embargo, ¿es la respuesta ideal al impulso una aproximación suficientemente precisa a la respuesta real y, de ser así, es precisa en todo el tiempo o en solo una parte del tiempo de respuesta?
6. ^{Si compara la Figura 2.4.1 para la función de paso de unidad Heaviside\(H(t)\) con la Figura 3.4.2 para la respuesta de paso de un sistema estable de primer orden, puede ver que a medida que la constante de tiempo\(\tau_{1}\) se vuelve progresivamente más pequeña, la respuesta de paso de primer orden se ve progresivamente más} como la función unidad-paso. Usando la ecuación 2.4.1 para\(H(t)\) como modelo, definamos la función “paso de unidad exponencial”\(H_{e}(t)\):\ [H (t) =\ left\ {\ begin {array} {ll}
   0 &\ text {for} t<0\\
   1 &\ text {for} t>0
   \ end {array}\ Rightarrow H_ {e} (t)\ equiv\ left\ {\ begin { array} {c}
   0\ quad\ text {for} t<0\\
   1-e^ {-t/\ tau_ {1}}\ quad\ text {for} t>0
   \ end {array}\ right. \ derecho. \ nonumber\] Está claro que se\(H(t)\) puede definir como un límite de\(H_{e}(t)\):\(H(t)=\lim _{\tau_{1} \rightarrow 0} H_{e}(t)\). Ahora, definamos la función “impulso-unidad-exponencial”\(\delta_{e}(t)\):\ [\ delta_ {e} (t)\ equiv\ left\ {\ begin {array} {c}
   0\ quad\ text {for} t<0\
   \ frac {d} {d} {d t}\ left (1-e^ {-t/\ tau_ {1}}\ right) =\ frac {1}\ tau_ {1}} e^ {-t/\ tau_ {1}}\ quad\ texto {para} t>0
   \ end {array}\ right. \ nonumber\] Esboza a mano un par de gráficas por encima y por debajo, siendo la gráfica superior\(H_{e}(t)\) vs.\(t\) y la gráfica inferior\(\delta_{e}(t)\) vs\(t\). Esbozar conceptualmente las dos funciones exponenciales para unos pocos valores de constante de tiempo\(\tau_{1}\); mostrar en particular cómo\(H_{e}(t)\) y\(\delta_{e}(t)\) evolucionar a medida que\(\tau_{1}\) se vuelve progresivamente más pequeño. Describir el carácter de\(\delta_{e}(t)\) como\(\tau_{1} \rightarrow 0\). ¿Es plausible físicamente definir la función delta de Dirac como\(\delta(t)=\lim _{\tau_{1} \rightarrow 0} \delta_{e}(t)\), que, con la definición\(H(t)=\lim _{\tau_{1} \rightarrow 0} H_{e}(t)\), equivale a\(\delta(t)=d H / d t\)? [Esta es una de las muchas definiciones posibles de proceso límite de\(\delta(t)\); la Ecuación 8.4.1 es una definición más utilizada.]
7. Considere el sistema masa-resorte (con amortiguación descuidada) de la Figura 1.10.1, para el cual es la ODE de movimiento\(m \ddot{x}+k x=f_{x}(t)\), y los parámetros del sistema son\(m\) = 2.20 kg y\(k\) = 770 N/m. Las condiciones iniciales son cero:\(x(0)\) = 0 y\(\dot{x}(0)\) = 0. La excitación es un impulso de fuerza exponencial en aumento\(f_{x}(t)=F_{m}\left(t / t_{m}\right) \exp \left(1-t / t_{m}\right)\), con\(F_m\) = 6.0 N y\(t_m\) = 1/12 s. Escriba un programa MATLAB, o adapte el código de Convolución-suma Ejemplo 2 en la Sección 8.11, para calcular y trazar una solución numérica aproximada\(x(t)\) durante el intervalo de tiempo\(0 \leq t \leq 1\) s. Ajuste el tamaño de paso de tiempo\(\Delta t\) y el número de pasos de tiempo en el intervalo de 1 s en su código hasta que la gráfica de su solución aproximada aparezca muy similar a la de la Figura 1.10.2 de la solución exacta correspondiente. Envíe su código de MATLAB y su gráfica final de respuesta.