9.2: ODE de forma estándar

Utilizando los conceptos y la notación desarrollados en la sección anterior, ahora derivamos la forma “estándar” de ODE que gobierna la respuesta de los sistemas de ^segundo orden amortiguados, comenzando con la Ecuación ODE 9.1.1 para un\(k\) sistema\(m\)\(c\) - -:

\[m \ddot{x}+c \dot{x}+k x=f_{x}(t) \Rightarrow \ddot{x}+2 \frac{c}{2 \sqrt{m k}} \sqrt{\frac{k}{m}} \dot{x}+\frac{k}{m} x=\frac{1}{m} f_{x}(t)=\frac{k}{m} \frac{f_{x}(t)}{k}\label{eqn:9.12} \]

Usando las definiciones de la sección anterior y la cantidad de entrada estándar Ecuación 7.1.4,\(u(t) \equiv f_{x}(t) / k\), reescribimos la ecuación\(\ref{eqn:9.12}\) en la forma estándar:

\[\ddot{x}+2 \zeta \omega_{n} \dot{x}+\omega_{n}^{2} x=\omega_{n}^{2} u(t)\label{eqn:9.13} \]

En Ecuación\(\ref{eqn:9.13}\),\(x(t)\) representa cualquier cantidad de salida apropiada (no necesariamente solo la posición como en la Figura 9.1.1 para un sistema amortiguado ^{de segundo} orden. Recordemos del Capítulo 7 que podemos identificar\(u(t)\) como siendo la salida pseudo-estática,\(x_{p s}(t)\); si\(x(t)\) varía lo suficientemente lentamente que los términos\(\ddot{x}\) y\(2 \zeta \omega_{n} \dot{x}\) son insignificantes en comparación con\(\omega_{n}^{2} x\), entonces la ecuación ODE\(\ref{eqn:9.13}\) reduce a una ecuación algebraica simple,\(\omega_{n}^{2} x \approx \omega_{n}^{2} u(t)\), cuya solución es la respuesta pseudo-estática,\(x(t)=u(t) \equiv x_{p s}(t)\).

Ejemplo\(\PageIndex{1}\): the \(LRC\) circuit, a 2^nd order electrical system

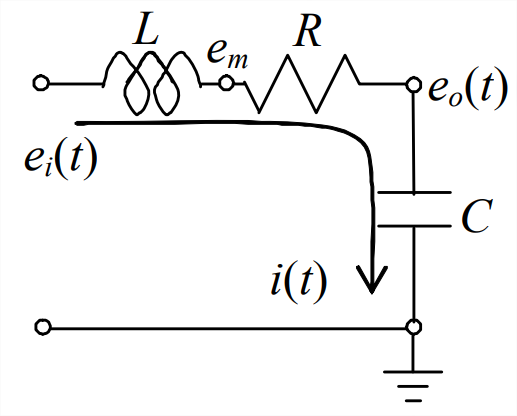
Derivamos una ODE que gobierna el comportamiento dinámico del\(LRC\) circuito en la siguiente figura. Para escribir la ley de voltaje de Kirchhoff para este circuito, comenzamos en el generador de voltaje de entrada y procedemos en sentido horario [ver Ecuación 5.2.10]:

\[\left(e_{i}-0\right)+\left(e_{m}-e_{i}\right)+\left(e_{o}-e_{m}\right)+\left(0-e_{o}\right)=0 \nonumber \]

A continuación, sustituimos en la Ecuación 5.2.9 el inductor y la ecuación 5.2.1 de la ley de Ohm para la resistencia:

\[e_{i}+\left(-L \frac{d i}{d t}\right)+(-R i)-e_{o}=0 \Rightarrow L \frac{d i}{d t}+R i+e_{o}=e_{i}(t) \nonumber \]

Para el condensador, usamos la Ecuación 5.2.6, luego diferenciamos el resultado y sustituimos en la ODE:

\[i=C \frac{d\left(e_{o}-0\right)}{d t}=C \dot{e}_{o} \Rightarrow \frac{d i}{d t}=C \ddot{e}_{o} \Rightarrow L C \ddot{e}_{o}+R C \dot{e}_{o}+e_{o}=e_{i}(t) \nonumber \]

Por lo tanto, podemos escribir la ODE en la forma estándar de 2 ^nd orden Ecuación\(\ref{eqn:9.13}\) como ¹

\[\ddot{e}_{o}+\frac{R}{L} \dot{e}_{o}+\frac{1}{L C} e_{o}=\frac{1}{L C} e_{i}(t) \nonumber \]

A partir de esta forma estándar, vemos que la frecuencia natural no amortiguada es\(\omega_{n}=1 / \sqrt{L C}\), y la relación de amortiguación viscosa es\(\zeta=\left(1 / 2 \omega_{n}\right)(R / L)=\frac{1}{2} R \sqrt{C / L}\).

Figura\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\): the rate gyroscope, a 2^nd order mechanical system

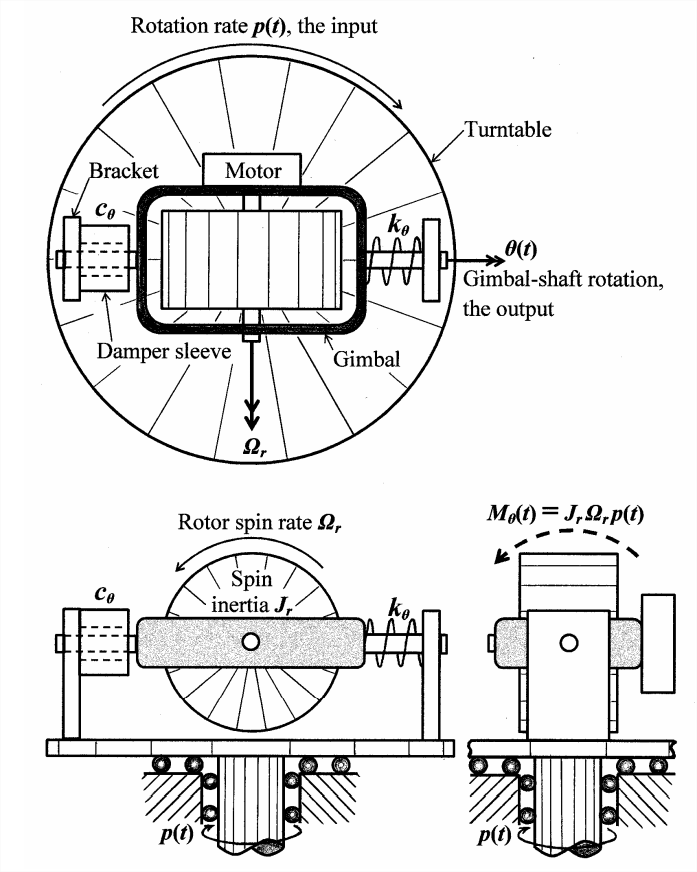
El boceto esquemático de ingeniería de tres vistas en la página siguiente representa la forma funcional básica de un giroscopio de velocidad de un solo eje (giroscopio), un sensor de velocidad de rotación ². El plato giratorio de soporte en el boceto podría ser un accesorio en una configuración de laboratorio para calibrar el sensor; el plato giratorio gira en sentido horario (como se ve desde arriba) con velocidad de rotación (velocidad)\(p(t)\). En el corazón del giroscopio de frecuencia se encuentra un rotor giratorio con inercia rotacional polar\(J_r\) alrededor de su eje de giro; es impulsado por un motor para girar en sentido antihorario (como se ve desde el frente) a la alta velocidad de giro constante (velocidad de rotación)\(\Omega_{r}\), que suele ser órdenes de magnitud mayores que\(|p(t)|\). El motor y el rotor giratorio están unidos a un cardán (bastidor giratorio) y segmentos de eje que encajan en cojinetes dentro de soportes que se proyectan desde la plataforma giratoria. El conjunto de eje cardán (incluyendo el motor y el rotor giratorio) puede girar a través de un pequeño ángulo\(\theta(t)\) alrededor del llamado “eje cardán”. Esta\(\theta(t)\) rotación es resistida por un resorte rotacional con constante\(k_{\theta}\), y por un amortiguador viscoso rotacional con constante\(c_{\theta}\). (El arrastre es impuesto por el líquido viscoso dentro de un espacio entre la superficie exterior del segmento del eje y la superficie interna del manguito, que está unido al soporte). La inercia de rotación polar del conjunto de cardán-eje alrededor del eje cardán es\(J_{\theta}\). Debido a la inercia\(J_{r}\) y la alta velocidad\(\Omega_{r}\) del rotor giratorio, la rotación del plato giratorio\(p(t)\) induce un momento inercial alrededor del eje cardán,\(M_{\theta}(t)=J_{r} \Omega_{r} p(t) \cos \theta(t)\) [como se deriva de las leyes de Newton de la dinámica de cuerpo rígido por, por ejemplo, Cannon, 1967, páginas 152-163]; suponemos que\(\theta(t)\) es lo suficientemente pequeño que\(\cos \theta(t) \approx 1\), así que\(M_{\theta}(t) \approx J_{r} \Omega_{r} p(t)\), como está etiquetado en el boceto. De la Ecuación 3.3.2, la ^segunda ley de Newton para la rotación del conjunto de eje cardán alrededor del eje cardán es

\[\Sigma(\text { Moments })_{\text {about } ~ g i m b a l ~ a x i s ~}=(\text { rotational inertia) } \times(\text { rotational acceleration) })_{\text{about gimbal axis}} \nonumber \]

\[M_{\theta}(t)-c_{\theta} \dot{\theta}-k_{\theta} \theta=J_{\theta} \ddot{\theta} \quad \Rightarrow \quad J_{\theta} \ddot{\theta}+c_{\theta} \dot{\theta}+k_{\theta} \theta=J_{r} \Omega_{r} p(t) \nonumber \]

Por lo tanto, podemos escribir la ODE en la forma estándar de 2 ^nd orden Ecuación\(\ref{eqn:9.13}\) como

\[\ddot{\theta}+\frac{c_{\theta}}{J_{\theta}} \dot{\theta}+\frac{k_{\theta}}{J_{\theta}} \theta=\frac{J_{r} \Omega_{r}}{J_{\theta}} p(t)=\frac{k_{\theta}}{J_{\theta}} \frac{J_{r} \Omega_{r}}{k_{\theta}} p(t) \nonumber \]

De esta forma estándar, vemos que la frecuencia natural no amortiguada es\(\omega_{n}=\sqrt{k_{\theta} / J_{\theta}}\), y la relación de amortiguación viscosa es\(\zeta=\left(c_{\theta} / J_{\theta}\right) /\left(2 \omega_{n}\right)\), y la cantidad de entrada estándar, con las mismas dimensiones que la salida del ángulo de rotación\(\theta(t)\), es\(u(t)=\left(J_{r} \Omega_{r} / k_{\theta}\right) p(t) \equiv \theta_{p s}(t)\), la salida pseudo-estática.

En la aplicación práctica de un giroscopio de velocidad, un transductor detecta la rotación del conjunto de eje cardán y genera una señal eléctrica proporcional a\(\theta(t)\), que podría ser visualizada y/o registrada por un sistema de adquisición y procesamiento de datos, y también podría servir como entrada a un sistema de control. Los giroscopios de velocidad de rotor giratorio vienen en varios tamaños y formas; las unidades típicas son del tamaño de una lata de verduras de una o dos libras, y sus cajas pueden ser cilíndricas o en forma de caja ³.

Figura\(\PageIndex{2}\)

¹ En el Apéndice B, Sección 19.3, esta ODE se deriva por un método alternativo que utiliza energía y potencia. La tasa de cambio de la energía del sistema se equipara con la energía suministrada al sistema.

Se han utilizado ² giroscopios en sensores y actuadores tanto para vehículos aeroespaciales como para vehículos acuáticos. Algunos ejemplos son descritos por Cannon, 1967, páginas 159-163, 617-626, 696-697, y por Den Hartog, 1956, páginas 108-112.

³ Este tipo de giroscopio de rotor giratorio puede considerarse un diseño “heredado”, no necesariamente el más moderno o el mejor para las aplicaciones actuales. Más recientemente se han desarrollado sensores de rotación que utilizan óptica láser y microelectromecánica (MEMS).