9.4: Respuesta transitoria IC de sistemas de segundo orden con poca amortiguación

Una forma de vibración transitoria y libre es la respuesta de condiciones iniciales no nulas, con entrada\(u(t)=0\) para todos los tiempos. Con\(u(t)=0\), las ecuaciones de respuesta 9.3.8 y 9.3.9 se convierten

\[x(t)=e^{-\zeta \omega_{n} t}\left[x_{0} \cos \omega_{d} t+\left(\frac{\dot{x}_{0}+\zeta \omega_{n} x_{0}}{\omega_{d}}\right) \sin \omega_{d} t\right], \text { for } 0 \leq t \text { and } 0 \leq \zeta<1\label{eqn:9.21a} \]

Siguiendo el procedimiento de las Ecuaciones 7.3.2-7.3.4 para combinar las dos sinusoides de la Ecuación\(\ref{eqn:9.21a}\), también podemos expresar la respuesta IC, libre-vibración como

\[x(t)=x_{\max } e^{-\zeta \omega_{n} t} \cos \left(\omega_{d} t+\phi\right), \text { for } 0 \leq t \text { and } 0 \leq \zeta<1\label{eqn:9.21b} \]

dónde\(x_{\max }=\sqrt{x_{0}^{2}+\left(\frac{\dot{x}_{0}+\zeta \omega_{n} x_{0}}{\omega_{d}}\right)^{2}}\) y\(\phi=\tan ^{-1}\left[-\left(\frac{\dot{x}_{0}+\zeta \omega_{n} x_{0}}{\omega_{d}}\right) / x_{0}\right]\)

Obsérvese que para\(\zeta=0\), responder Ecuaciones\(\ref{eqn:9.21a}\) y\(\ref{eqn:9.21b}\) reducir a los resultados Ecuación 7.3.1 y Ecuación 7.3.4 derivadas para un sistema sin amortiguar en el Capítulo 7. Al respecto, es útil tener presente la definición de la frecuencia natural amortiguada,\(\omega_{d} \equiv \omega_{n} \sqrt{1-\zeta^{2}}\).

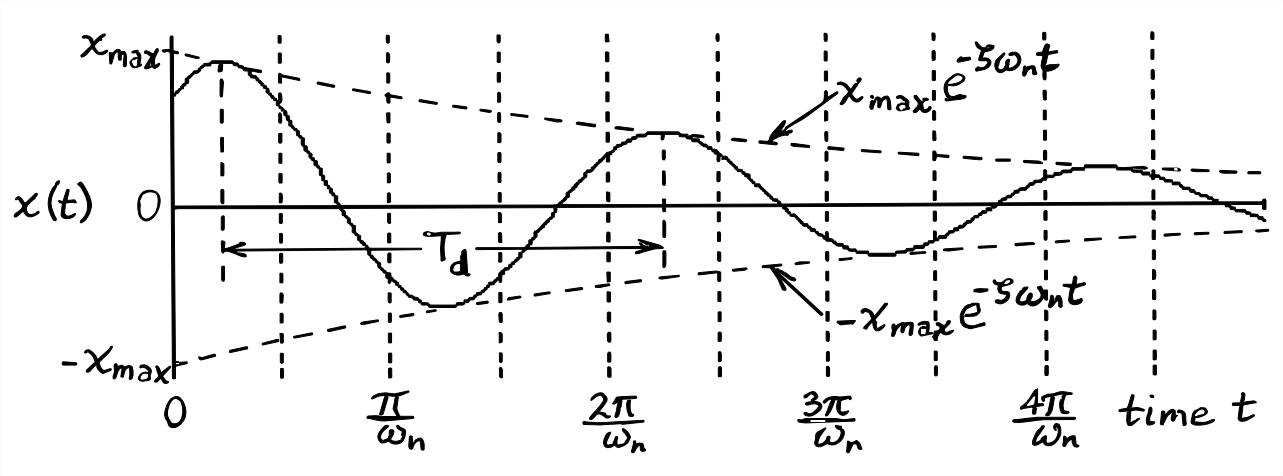
La ecuación\(\omega_{d} \equiv \omega_{n} \sqrt{1-\zeta^{2}}\) también muestra que el amortiguamiento reduce la frecuencia de vibración libre, y aumenta el periodo,\(T_{d} \equiv 2 \pi / \omega_{d}\). Sin embargo, las palabras “frecuencia” y “período” se usan de manera floja en este caso, porque la respuesta amortiguada no es verdaderamente periódica. Más correctamente,\(T_{d}\) se define como el tiempo entre crestas o decesos locales sucesivos de la respuesta, y entre ceros sucesivos de sentido positivo o negativo.

La figura\(\PageIndex{2}\) de la siguiente página es un boceto anotado de ecuaciones de respuesta\(\ref{eqn:9.21a}\) y\(\ref{eqn:9.21b}\) para valores positivos de los CI,\(x_{0}>0\) y\(\dot{x}_{0}>0\), y para la relación de amortiguación pequeña\(\zeta=0.11\). La salida es una sinusoide,\(\cos \left(\omega_{d} t+\phi\right)\), modulada por una envolvente exponencial en decadencia,\(\pm x_{\max } e^{-\zeta \omega_{n} t} \equiv \pm x_{\max } e^{-t / \tau_{2}}\). En esta ecuación para la envolvente exponencial, definimos la constante de tiempo\(\tau_{2}\) apropiada para los sistemas de ^segundo orden subamortiguados como

\[\tau_{2} \equiv \frac{1}{\zeta \omega_{n}}\label{eqn:9.22} \]

Figura\(\PageIndex{1}\): Respuesta IC de un sistema amortiguado ^{de segundo} orden,\(\zeta = 0.11\)

A menudo es necesario medir experimentalmente la respuesta dinámica de los sistemas mecánicos, lo que requiere sensores (transductores) que detectan una cantidad de respuesta y la convierten en una tensión eléctrica. Los sensores más abundantes y relativamente económicos para los sistemas mecánicos son los acelerómetros de traslación (ver tarea Problema 10.12). También se utilizan sensores de velocidad y sensores de traslación (desplazamiento), pero con menos frecuencia. Es apropiado, por lo tanto, que encontremos a partir de ecuaciones de “desplazamiento”\(\ref{eqn:9.21a}\) y\(\ref{eqn:9.21b}\) las ecuaciones correspondientes para la “velocidad” y la “aceleración” de vibración libre. Una diferenciación de la ecuación\(\ref{eqn:9.21b}\) da

\[\dot{x}(t)=x_{\max } e^{-\zeta \omega_{n} t}\left[-\zeta \omega_{n} \cos \left(\omega_{d} t+\phi\right)-\omega_{d} \sin \left(\omega_{d} t+\phi\right)\right] \nonumber \]

A continuación, combinamos los dos términos sinusoidales con el uso de la identidad trigonométrica\(\sin A \cos B+\cos A \sin B=\sin (A+B)\) y la ecuación\(\omega_{d} \equiv \omega_{n} \sqrt{1-\zeta^{2}}\), conduciendo a

\[\dot{x}(t)=-\omega_{n} x_{\max } e^{-\zeta \omega_{n} t} \sin \left(\omega_{d} t+\phi+\sin ^{-1} \zeta\right), \text { for } 0 \leq t \text { and } 0 \leq \zeta<1\label{eqn:9.23} \]

Una diferenciación más de la ecuación\(\ref{eqn:9.23}\) seguida de un procedimiento de combinación similar da

\[\ddot{x}(t)=-\omega_{n}^{2} x_{\max } e^{-\zeta \omega_{n} t} \cos \left(\omega_{d} t+\phi+2 \sin ^{-1} \zeta\right), \text { for } 0 \leq t \text { and } 0 \leq \zeta<1\label{eqn:9.24} \]

Vemos que el desplazamiento, la velocidad y la aceleración tienen la misma forma sinusoidal amortiguada. Por lo tanto, las mediciones experimentales de cualquiera de las tres pueden ser utilizadas para la identificación de parámetros del sistema tales como\(\zeta\) y\(\omega_d\), un tema abordado en secciones posteriores.