9.5: Cálculo de la relación de amortiguación viscosa

Considere un sistema de ^segundo orden amortiguado en un estado de vibración libre, es decir, con entrada cero,\(u(t)=0\). Esta vibración libre puede ser una respuesta de condición inicial o la respuesta residual después de que haya cesado la excitación de entrada, por ejemplo, para\(t>t_{d}\) si la entrada es un pulso. Entonces la libre decadencia tendrá la forma de Figura\(\PageIndex{1}\). En la figura,\(x\left(t_{0}\right) \equiv x_{0}\) se anota un valor extremo local de referencia (en una cresta en la figura\(\PageIndex{1}\), pero bien podría estar en un comedero), y también se anotan los valores extremos locales posteriores (tanto crestas como canales). Deseamos calcular la relación de amortiguación viscosa\(\zeta\) a partir de la gráfica de respuesta. Obsérvese también que la envolvente exponencial se indica en la Figura\(\PageIndex{1}\) con líneas discontinuas.

Figura\(\PageIndex{1}\): Respuesta de vibración libre de un sistema amortiguado ^{de segundo} orden

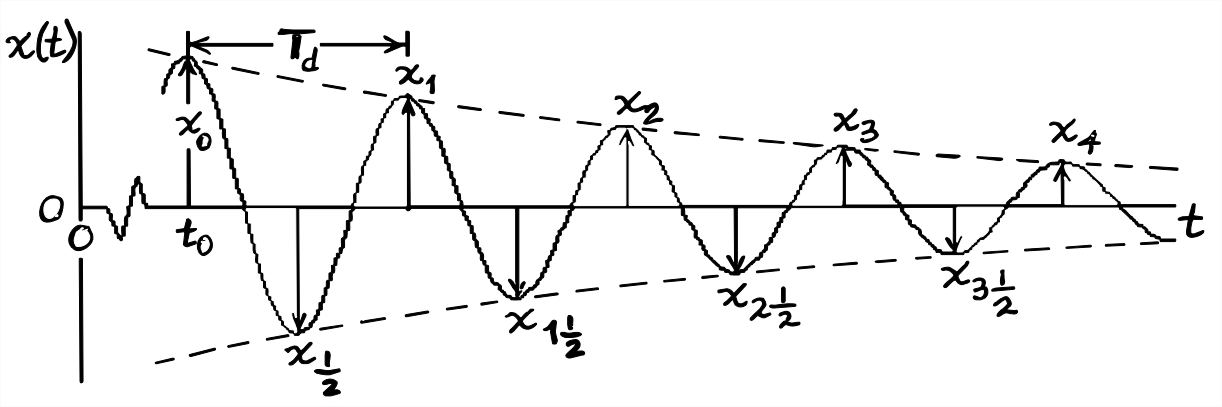
Utilizamos la ecuación\(\ref{eqn:9.21b}\) para una respuesta de vibración libre:

\[x(t)=x_{\max } e^{-\zeta \omega_{n} t} \cos \left(\omega_{d} t+\phi\right)\label{eqn:9.21b} \]

A partir de esta ecuación, formamos la relación\(x_{0} / x_{r}\) del valor absoluto extremo de referencia\(\left|x\left(t_{0}\right)\right|\) dividido por la\(r\) ^ésima cresta o valor absoluto mínimo, donde\(r\) como se muestra en la Figura\(\PageIndex{1}\) puede tener valores enteros o semienteros. Tenga\(\left|\cos \left(\omega_{d} t+\phi\right)\right|=1\) en cuenta que en cada uno de los valores extremos locales, y que el tiempo del valor extremo\(r\) ^th es\(t_{r}=t_{0}+r T_{d}\), donde\(T_d = 2 \pi / \omega_{d}\) está el periodo natural amortiguado. Entonces la relación requerida es

\[\frac{x_{0}}{x_{r}}=\frac{e^{-\zeta \omega_{n} t_{0}}}{e^{-\zeta \omega_{n}\left(t_{0}+r T_{d}\right)}}=e^{\zeta \omega_{n} r T_{d}}=\exp \left(\zeta \omega_{n} r \frac{2 \pi}{\omega_{n} \sqrt{1-\zeta^{2}}}\right)=\exp \left(2 \pi r \frac{\zeta}{\sqrt{1-\zeta^{2}}}\right)\label{eqn:9.25} \]

Tomando el logaritmo natural de la Ecuación\(\ref{eqn:9.25}\) da el llamado decremento logarítmico:

\[\ln \left(\frac{x_{0}}{x_{r}}\right)=2 \pi r \frac{\zeta}{\sqrt{1-\zeta^{2}}} \Rightarrow \frac{\zeta}{\sqrt{1-\zeta^{2}}}=\frac{\ln \left(x_{0} / x_{r}\right)}{2 \pi r} \equiv \zeta_{s}\label{eqn:9.26} \]

En el último término de la Ecuación\(\ref{eqn:9.26}\), definimos\(\zeta_s\) como el aproximado para la relación de amortiguación “pequeña”\(zeta\). Es muy común que un sistema tenga amortiguación positiva, pero pequeña. Definimos que la amortiguación es pequeña si\(\sqrt{1-\zeta^{2}} \approx 1\), lo que simplifica considerablemente ecuaciones como la Ecuación\(\ref{eqn:9.26}\). Porque\(\zeta=0.2\),\(\sqrt{1-\zeta^{2}}=0.980\), entonces este es un límite superior razonable para la “pequeñez”. Podemos encontrar la ecuación exacta para\(\zeta\) al cuadrar Ecuación\(\ref{eqn:9.26}\) y luego proceder algebraicamente para derivar

\[\zeta=\frac{\zeta_{s}}{\sqrt{1+\zeta_{s}^{2}}}, \text { for } 0 \leq \zeta<1\label{eqn:9.27} \]

Podría parecer que la derivación anterior requiere que los valores de\(x_0\) y\(x_r\) estén en crestas y bajadas de la gráfica de respuesta, y que estos deben ser valores de cero a pico; pero ninguna de estas restricciones es necesaria. Los valores de\(x_0\) y\(x_r\) pueden estar en cualquier instante conveniente a lo largo de la historia del tiempo (ceros de la respuesta, así como extremos), siempre que interpretemos\(x_0\) y\(x_r\) como siendo las magnitudes de la envolvente exponencial en los instantes elegidos. Normalmente, solo está disponible la gráfica de respuesta de vibración libre (de un osciloscopio de almacenamiento, grabadora de gráficos de banda, etc.), por lo que debemos bosquejar en la envolvente exponencial para ayudar en la medición\(x_0\),\(x_r\) y\(r\). Además, en lugar de medir valores de cero a pico, es más preciso y más fácil de medir\(x_0\) y\(x_r\) como valores pico a pico, desde el límite exponencial inferior hasta el límite exponencial superior.

Resumamos el procedimiento para medir/calcular\(\zeta\) a partir de una gráfica de respuesta de vibración libre. Primero, bosquejo en la envolvente exponencial. A continuación, elija instantes de tiempo a lo largo de la gráfica en los que pueda medir con una precisión razonable el número de períodos\(r\) (generalmente un entero, semientero o un cuarto entero) y las magnitudes\(x_0\) y\(x_r\) entre los límites exponenciales. A continuación, sustituya los valores medidos de\(r\),\(x_0\), y\(x_r\) en Ecuación\(\ref{eqn:9.26}\) y calcule\(\zeta_s\). Si esto\(\zeta_{s}\) es\(\leq 0.2\), entonces\(\zeta \approx \zeta_{s}\) con suficiente precisión de ingeniería. Sin embargo, si\(0.2<\zeta_{s}<1\), entonces calcula con\(\zeta\) mayor precisión a partir de la Ecuación\(\ref{eqn:9.27}\).

Existe una versión simplificada de Ecuación\(\ref{eqn:9.26}\) que a menudo se utiliza para el cálculo rápido de pequeños\(\zeta\). Si es posible, encontramos la magnitud de referencia y la magnitud\(r\) ^th tal que\(x_{0} / x_{r}=2\), y etiquetamos el número de periodos como\(r_{1 / 2}\). De ahí,\(\ln \left(x_{0} / x_{r}\right) / 2 \pi \equiv 0.110\), lo que nos lleva de la Ecuación\(\ref{eqn:9.26}\) a la fórmula de media amplitud para pequeños\(\zeta\):

\[\zeta_{s}=\frac{0.110}{r_{1 / 2}} \approx \zeta\label{eqn:9.28} \]

Finalmente, la derivación anterior se basó en la Ecuación\(\ref{eqn:9.21b}\) para la respuesta de “desplazamiento”\(x(t)\). Sin embargo, las fórmulas derivadas para\(\zeta\) son igualmente válidas si las mediciones se realizan a partir de gráficas de “velocidad”\(\dot{x}(t)\) o “aceleración”\(\ddot{x}(t)\). Esto es así porque, a partir de las Ecuaciones 9.4.5 y 9.4.6, las derivadas de\(x(t)\) tienen la misma forma sinusoidal exponencialmente limitada que\(x(t)\) ella misma.