9.8: Especificaciones de respuesta escalonada para sistemas de amortiguación insuficiente

Los sistemas de ingeniería a menudo se diseñan de manera que el historial de tiempo de una cantidad de salida imite lo más cerca posible el historial de tiempo de la cantidad de entrada. Un ejemplo, con referencia a la Sección 3.5, es el balanceo inducido por alerón de un avión, para lo cual la entrada original es el ángulo de rueda de control establecido manualmente (“ordenado”) por el piloto, y la salida final es la velocidad de balanceo del avión. Otro ejemplo es el automóvil moderno; generalmente describimos un automóvil como “sensible” si la dirección (o la aceleración, o el frenado) imita rápida y precisamente los comandos del conductor establecidos a mano o a pie.

La respuesta escalonada de un sistema se utiliza a menudo para medir y cuantificar la “capacidad de respuesta” dinámica. Idealmente, la respuesta escalonada imitaría exactamente la entrada de paso, pero las características del sistema como la inercia y la amortiguación evitan dicha respuesta instantánea. El grado en que la respuesta escalonada no logra imitar la entrada de paso se cuantifica en las siguientes cuatro especificaciones de respuesta escalonada: tiempo de subida,\(t_{r}\); tiempo pico\(t_{p}\), relación máxima de sobreimpulso,\(\bar{x}_{p}\), y tiempo de asentamiento,\(t_{s}\). Estas cantidades de respuesta escalonada se ilustran en la Figura 9.6 de la página siguiente. Se les llama “especificaciones” o “especificaciones” porque es común al inicio de un proyecto especificarlas como objetivos de diseño; posteriormente, estas cantidades de respuesta escalonada se miden experimentalmente en prototipos y/o artículos de prueba de producción.

Figura\(\PageIndex{1}\): Especificaciones de respuesta escalonada de un sistema de amortiguación insuficiente

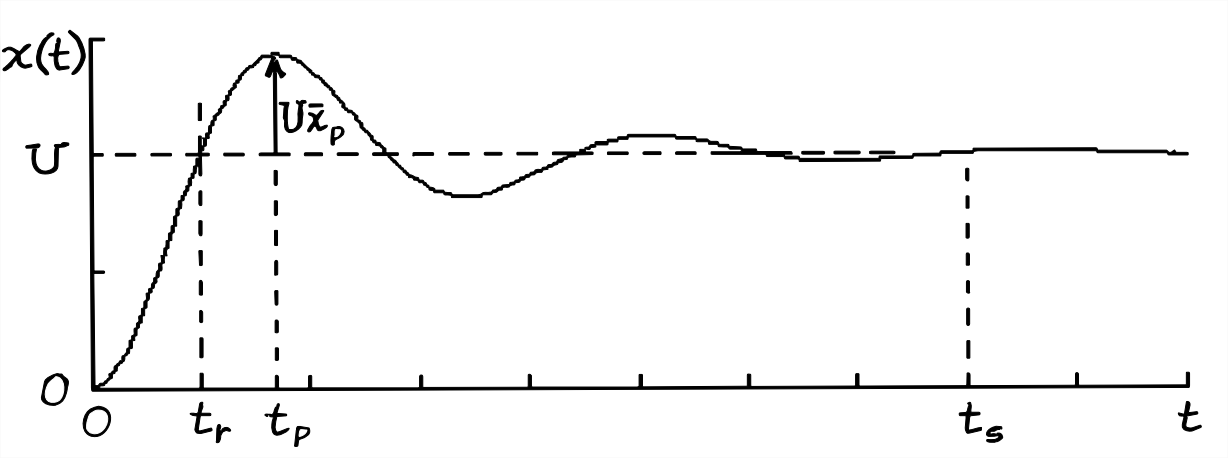
Para sistemas de ^segundo orden subamortiguados, podemos aplicar la solución de respuesta escalonada Ecuación 9.6.5 y la solución impulso-respuesta Ecuación 9.7.2 para derivar ecuaciones específicas para las especificaciones de respuesta escalonada:

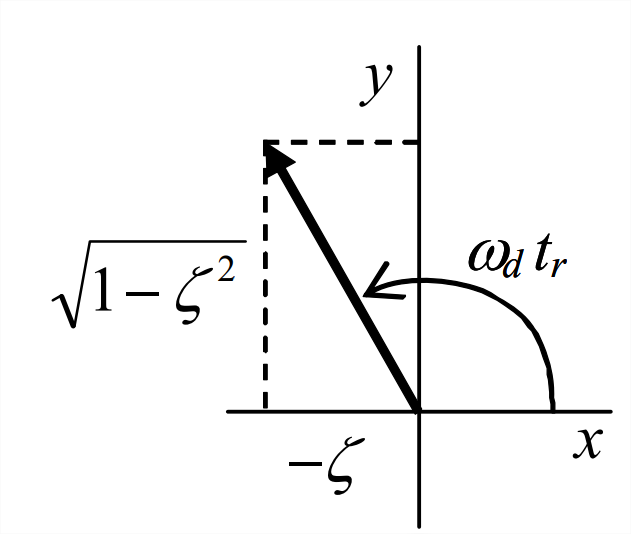
• De la Figura\(\PageIndex{1}\), evaluamos la Ecuación 9.6.5 en\(t=t_{r}\), la primera vez cuando\(x(t) = U\):\[x\left(t_{r}\right)=U=U\left[1-e^{-\zeta \omega_{n} t_{r}}\left(\cos \omega_{d} t_{r}+\frac{\zeta \omega_{n}}{\omega_{d}} \sin \omega_{d} t_{r}\right)\right] \Rightarrow \cos \omega_{d} t_{r}+\frac{\zeta \omega_{n}}{\omega_{d}} \sin \omega_{d} t_{r}=0 \nonumber \]\[\Rightarrow \tan \omega_{d} t_{r}=-\frac{\omega_{d}}{\zeta \omega_{n}}=-\frac{\sqrt{1-\zeta^{2}}}{\zeta}=-\frac{1}{\zeta_{s}} \nonumber \] Esta última ecuación muestra que\(\zeta \rightarrow 0\) a partir de valores positivos, luego\(\tan \omega_{d} t_{r} \rightarrow-\infty\) a partir de valores negativos; por lo tanto,\(\omega_{d} t_{r} \rightarrow \frac{1}{2} \pi \times n\) a partir de valores más altos, donde\(n = 1, 5, 9, \dots\); y primera vez cuando\(x(t) = U\) corresponde a\(n = 1\): a\(\omega_{d} t_{r} \rightarrow \frac{1}{2} \pi\) partir de valores superiores. Esto lo podemos ver en la Figura 9.6.1, donde\(t_{r}\) es justo un poco después\(\frac{1}{2} \pi / \omega_{n}\) (tenga en cuenta eso\(\omega_{d} \leq \omega_{n}\)). Esto lleva a la conclusión de que el tiempo de subida viene dado por \[t_{r}=\frac{1}{\omega_{d}} \tan ^{-1}\left(\frac{\sqrt{1-\zeta^{2}}}{-\zeta}\right)\label{eqn:9.33} \]En Ecuación\(\ref{eqn:9.33}\), tomamos el valor de la tangente inversa de cuatro cuadrantes que está entre\(\frac{1}{2} \pi\) y\(\pi\), como se muestra en el dibujo a continuación.

  

  Figura\(\PageIndex{2}\)

• De Figura\(\PageIndex{1}\),\(t_p\) es el tiempo en el que\(x(t)\) es máximo y la primera vez después de\(t = 0\) eso\(t= 0\). Entonces necesitamos diferenciar la Ecuación 9.6.5, ponerla en cero, y resolver para a\(t_p\) partir de la ecuación resultante. A partir de la aparición de la Ecuación 9.6.5, sin embargo, esa diferenciación será larga y tediosa. Pero ese trabajo penoso no será necesario, porque una relación fundamental derivada en la Sección 8.7 vendrá a nuestro rescate. Identificamos la respuesta unidad-paso como Ecuación 9.6.5 con magnitud de paso\(U = 1\): \[x_{H}(t)=1 \times\left[1-e^{-\zeta \omega_{n} t}\left(\cos \omega_{d} t+\frac{\zeta \omega_{n}}{\omega_{d}} \sin \omega_{d} t\right)\right]=1-e^{-\zeta \omega_{n} t}\left(\cos \omega_{d} t+\frac{\zeta \omega_{n}}{\omega_{d}} \sin \omega_{d} t\right)\label{eqn:9.34} \]Claramente,\(t_p\) es independiente de la magnitud del paso\(U\). Ahora, la Ecuación 8.6.6 da la derivada de la Ecuación\(\ref{eqn:9.34}\) as\(d x_{H} / d t=h(t)\), donde el IRF\(h(t)\) en este caso es la Ecuación 9.7.3. Por lo tanto, la ecuación que conduce a lo que buscamos es \[\frac{d x_{H}}{d t}=h(t)=\frac{\omega_{n}^{2}}{\omega_{d}} e^{-\zeta \omega_{n} t} \sin \omega_{d} t=0 \text { at } t=t_{P}\label{Eqn:9.35} \]La solución requerida de Ecuación\(\ref{eqn:9.35}\) es el valor positivo más bajo de lo\(t\) que satisface\(\sin \omega_{d} t= 0\), que es \[t_{p}=\frac{\pi}{\omega_{d}}\label{eqn:9.36} \]El equivalente gráfico de esta derivación matemática de Ecuación\(\ref{eqn:9.36}\) es evidente en un examen de las Figuras 9.6.1 y 9.7.1, donde podemos ver que tanto el pico de la respuesta escalonada como el primer cero de la respuesta de impulso ideal ocurren en un instante\(t\) justo un poco después\(\pi / \omega_{n}\) (recordemos eso\(\omega_{d} \leq \omega_{n}\)).
• De la Figura\(\PageIndex{1}\), la Ecuación 9.6.5 y la Ecuación\(\ref{eqn:9.36}\), la relación de sobreimpulso máxima es\[\bar{x}_{p}=\frac{x\left(t_{p}\right)-U}{U}=-e^{-\zeta \omega_{n} t_{p}}\left(\cos \omega_{d} t_{p}+\frac{\zeta \omega_{n}}{\omega_{d}} \sin \omega_{d} t_{p}\right)=-\exp \left(-\zeta \omega_{n} \frac{\pi}{\omega_{d}}\right)\left(\cos \pi+\frac{\zeta \omega_{n}}{\omega_{d}} \sin \pi\right) \nonumber \] \[\Rightarrow \quad \bar{x}_{p}=\exp \left(-\frac{\zeta}{\sqrt{1-\zeta^{2}}} \pi\right) \leq 1, \text { valid for } 0 \leq \zeta<1\label{eqn:9.37} \]Así que la relación de sobreimpulso máxima es una función solo de la relación de amortiguación viscosa\(\zeta\). Por el contrario, se\(\zeta\) puede determinar a partir de una medición de\(\bar{x}_{p}\) tomando el logaritmo natural de la Ecuación\(\ref{eqn:9.37}\): \[\ln \bar{x}_{p}=-\frac{\zeta}{\sqrt{1-\zeta^{2}}} \pi \Rightarrow-\frac{\ln \bar{x}_{p}}{\pi}=\frac{\zeta}{\sqrt{1-\zeta^{2}}} \equiv \zeta_{s}, \text { valid for } 0<\bar{x}_{p} \leq 1\label{eqn:9.38} \]Observe la similitud de la Ecuación\(\ref{eqn:9.38}\) a la Ecuación 9.5.3 para el decremento logarítmico. Por lo tanto, volvemos a llegar a la Ecuación 9.5.4, la ecuación exacta que da\(\zeta\) para cualquier sobreimpulso en el rango\(0<\bar{x}_{p} \leq 1\):\(\zeta=\zeta_{s} / \sqrt{1+\zeta_{s}^{2}}\), para\(0 \leq \zeta<1\), ahora con\(\zeta_{s}=-\ln \bar{x}_{p} / \pi\).

  Si la amortiguación es pequeña tal que\(\sqrt{1-\zeta^{2}} \approx 1\), es decir,\(0 \leq \zeta \leq 0.2\), entonces Ecuaciones\(\ref{eqn:9.37}\) y\(\ref{eqn:9.38}\) se aproximan como: \[\bar{x}_{p} \approx e^{-\zeta \pi} \quad \text { and } \quad \zeta \approx-\frac{\ln \bar{x}_{p}}{\pi} \quad \text { valid for } 0 \leq \zeta \leq 0.2 \text { and } 0.534 \leq \bar{x}_{p} \leq 1\label{eqn:9.39} \]

• Esta especificación se define como el tiempo requerido para\(x(t)\) que la respuesta se asiente dentro\(\pm 2%\) del valor final de estado estacionario (pseudo-estático),\(U\). Para este sistema de ^segundo orden subamortiguado, la constante de tiempo de la envolvente exponencial es la Ecuación 9.4.3,\(\tau_{2} \equiv 1 / \zeta \omega_{n}\). Del Capítulo 3, tenemos\(1-e^{-4}=0.982\) (ver Figura 3.4.2), por lo que el tiempo de asentamiento se define como \[t_{s}=4 \tau_{2} \equiv \frac{4}{\zeta \omega_{n}}\label{eqn:9.40} \]

  Aquí es apropiado evaluar la variación en la respuesta escalonada de un sistema estándar de orden ² a medida que varía la amortiguación. La figura\(\PageIndex{3}\) de la siguiente página muestra respuestas ^{de paso de segundo} orden para un rango de relaciones de amortiguación viscosa\(\zeta\). [Las curvas de respuesta de la Figura\(\PageIndex{3}\) se calculan de la siguiente manera: para subamortiguamiento\(0 \leq \zeta<1\),, a partir de la Ecuación 9.6.5; para amortiguación crítica\(\zeta=1\),, a partir del resultado de la tarea Problema 9.11; para sobreamortiguación,\(\zeta=1.2\), a partir del resultado de la tarea Problema 9.16. La referencia de tiempo es periodo natural sin amortiguar\(T_{n}=2 \pi / \omega_{n}\).] Como ingenieros que diseñan un sistema, es posible que deseemos diseñar en el sistema una cantidad de amortiguación\(\zeta\) que haga que el historial de tiempo de una cantidad de salida imite lo más cerca posible el historial de tiempo de la cantidad de entrada. Esto significa que, en el contexto de la respuesta escalonada, querríamos tanto hacer que el tiempo de subida sea lo más rápido posible como minimizar el sobreimpulso. Sin embargo, la Figura\(\PageIndex{3}\) muestra que no podemos hacer ambas cosas simultáneamente para un sistema de ^segundo orden estándar: el tiempo de subida es el más rápido para los pequeños\(\zeta\), pero el sobreimpulso se minimiza o elimina con mayores\(\zeta\). Por lo tanto, tendríamos que comprometer y seleccionar un valor\(\zeta\) que produzca valores prácticamente aceptables tanto de tiempo de subida como de sobreimpulso, aunque ninguno de los parámetros de respuesta sería el mejor posible. Observe a partir de la Figura\(\PageIndex{3}\) que el sobreimpulso existe solo para la subamortiguación.

  

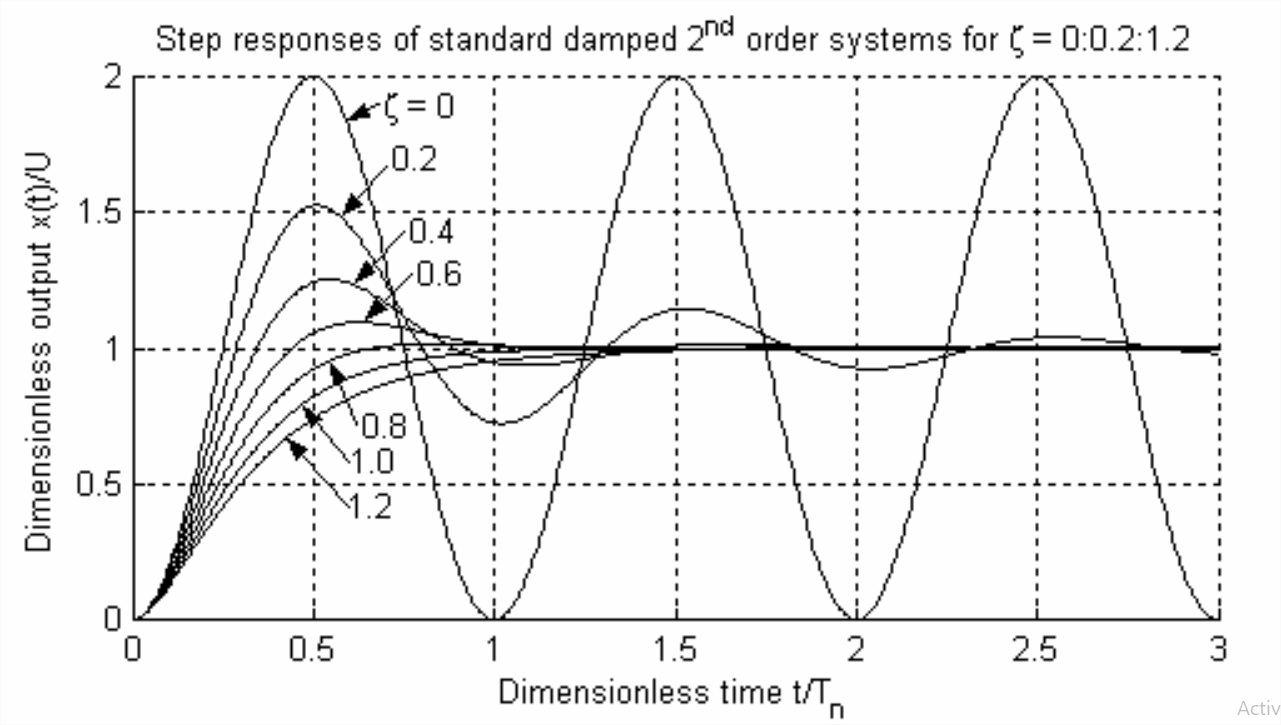
  Figura\(\PageIndex{3}\): Respuestas escalonadas de los sistemas estándar de ^segundo orden a medida que varía la amortiguación viscosa

  La respuesta transitoria de los sistemas de control de ingeniería es muy importante en la práctica, por lo que hay más análisis y discusión de temas como el tiempo de subida y el sobreimpulso más adelante en el libro, comenzando en el Capítulo 14.