9.11: Capítulo 9 Tarea

1. En el sistema dibujado a continuación, la masa\(m\) se une a un soporte móvil mediante amortiguador viscoso\(c_1\) y resorte\(k\), y la masa también se desliza sobre una superficie lubricada, lo que provoca una amortiguación viscosa con constante\(c_2\). Hay dos cantidades de entrada independientes: La cantidad de salida es el desplazamiento\(x(t)\) de la masa. Dibuje y etiquete diagramas de cuerpo libre claramente apropiados, luego use su FBD para derivar la ecuación diferencial de movimiento\(x(t)\) en términos de constantes\(m\),\(c_1\),\(c_2\) y\(k\), y entradas variables\(x_{i}(t)\) y\(f_{x}(t)\). Su ODA de movimiento debe incluir algunas dinámicas no estándar del lado derecho.

   

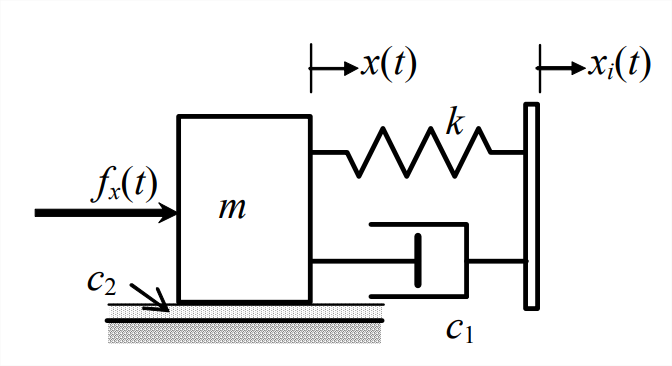
   Figura\(\PageIndex{1}\)

   1. desplazamiento de soporte\(x_{i}(t)\) mostrado (control de desplazamiento, por ejemplo, mediante una leva), que a menudo se denomina excitación de base ¹, y
   2. fuerza\(f_{x}(t)\) mostrada.
2. Dado, un\(k\) sistema estándar\(m\) -\(c\) -, Figura 9.1.1, con los siguientes parámetros: peso de la masa\(W=0.386\) lb, de manera que\(m=\frac{W}{g}=\frac{0.386 \mathrm{lb}}{386 \mathrm{inch} / \mathrm{s}^{2}}=0.001 \frac{\mathrm{lb}-\mathrm{s}^{2}}{\text { inch }}\); constante viscosa del amortiguador\(c=1.1 \times 10^{-3}\) lb/pulgada/s; constante de rigidez elástica\(k=3.025\) lb/pulgada.
   1. Calcular las siguientes cantidades, todas hasta al menos 3 cifras significativas:\(\omega_{n}\) en rad/s,\(f_{n}\) en Hz,\(\zeta\),\(\omega_{d}\) en rad/s,\(f_d\) en Hz, y\(T_{d} \equiv 1 / f_{d}\). Puede calcular estas cantidades en MATLAB, si lo desea, utilizando el formato de comando short e.
   2. Dadas las condiciones iniciales\(x(0)=0.5\) pulgadas y\(\dot{x}(0)=35\) pulgadas/s, calcule y grafique con MATLAB la respuesta de vibración libre debida a los CI durante aproximadamente 20 ciclos completos de descomposición. Dado que está multiplicando las funciones de tiempo sinusoidales por una función de tiempo exponencial, es necesario que utilice la multiplicación de matriz (.*) en MATLAB. Dibuja cuadrículas en tu gráfica y agrega un título apropiado y etiquetas de eje apropiadas.
   3. Dibuje a mano la envolvente exponencial en su gráfica, luego use las cuadrículas y/o un borde recto graduado para medir amplitudes de picos locales de la sinusoide en descomposición. En particular, encontrar (aproximadamente) la cantidad\(r_{1 / 2} \equiv\) el número de ciclos en descomposición a decaimiento a media amplitud (no necesariamente un número entero). Ahora calcule la relación adimensional\(0.110 / r_{1 / 2}\); el valor que calcule debe coincidir estrechamente con su valor calculado previamente de\(\zeta\).
3. La respuesta de vibración libre a las condiciones iniciales de un sistema de ^segundo orden amortiguado estándar viene dada por\(x(t)=2.24 e^{-0.300 t} \cos (12.00 t-1.11)\) mm, donde\(t\) es en segundos. Calcular
   1. la frecuencia natural amortiguada\(f_{d}\) en Hz,
   2. la constante de tiempo de amortiguación\(\tau_{2}\) en segundos, y
   3. la relación de amortiguación viscosa\(\zeta\) (use la\(\zeta\) aproximación pequeña). Muestra tus cálculos.
4. Un tipo simple de prueba de vibración que a menudo se usa para sistemas mecánicos poco amortiguados, como el\(k\) sistema\(m\)\(c\) - - de la Figura 9.1.1, se llama prueba de twang (llamado así por el sonido agudo y sonado que se produce al desplumar una cuerda de un instrumento musical; la Sección 7.6 demuestra twang prueba de una viga flexible): la masa se desplaza de su posición de equilibrio estático por cantidad\(x_{0}\) (con velocidad inicial cero,\(\dot{x}_{0}=0\)), luego se libera. A partir del registro de respuesta transitoria posterior, podemos calcular directamente la frecuencia natural amortiguada\(f_d\) y la relación de amortiguación viscosa\(\zeta\). Si conocemos inicialmente ya sea la masa\(m\) o la constante de rigidez\(k\), entonces podemos usar la medida\(f_d\) y\(\zeta\) para calcular la otra constante y la constante efectiva de amortiguación viscosa\(c\). Use la Ecuación 9.4.2 para mostrar que la respuesta de la prueba de twang es\[x(t)=x_{\max } e^{-\zeta \omega_{n} t} \cos \left(\omega_{d} t+\phi\right), \text { for } 0 \leq t \text { and } 0 \leq \zeta<1 \nonumber \] dónde\(x_{\max }=x_{0} / \sqrt{1-\zeta^{2}}\) y\(\phi=\tan ^{-1}(-\zeta / \sqrt{1-\zeta^{2}})\) Para un sistema muy ligeramente amortiguado, la aproximación simple preferida de esta respuesta de twang es\[x(t) \approx x_{0} e^{-\zeta \omega_{n} t} \cos \left(\omega_{n} t\right), \text { with } \phi \approx 0 \nonumber \] Cuán pequeña debe\(\zeta\) ser para que el retraso\(\phi\) de fase sea tan pequeño (digamos,\(|\phi| \leq 5^{\circ}\)) que no se puede distinguir del retraso de fase cero,\(\phi \approx 0\)? [NOTA: la resolución de medición en un registro gráfico analógico típico de respuesta de vibración de decaimiento transitorio (por ejemplo, desde una pequeña pantalla de osciloscopio) es tan limitada que la resolución de la fase calculada es probablemente solo alrededor\(\pm 5^{\circ}\).
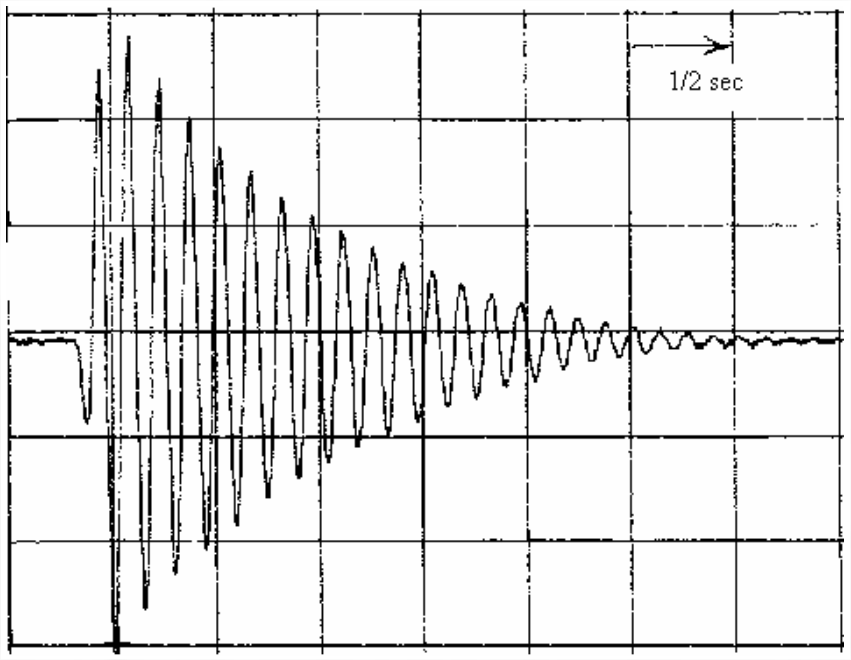
5. Se puso en movimiento un sistema de masa-amortiguador-resorte de laboratorio y luego se dejó vibrar libremente. La aceleración de la historia del tiempo en la página siguiente fue percibida por un acelerómetro ligero unido a la masa. El gráfico se copió de la pantalla de un osciloscopio digital. Calcular a partir de mediciones en una fotocopia de la gráfica la frecuencia natural amortiguada\(f_d\) (Hz) =\(\omega_{d} / 2 \pi\) y la relación de amortiguación viscosa\(\zeta\). Para obtener valores razonablemente precisos para\(f_d\) y\(\zeta\), asegúrese de promediar durante muchos ciclos de la sinusoide amortiguada. Para calcular\(\zeta\), primer boceto en la envolvente exponencial. También, tenga en cuenta que el nivel cero de la señal de aceleración está desplazado de la línea de rejilla horizontal central; por lo tanto, las mediciones de amplitud pico a pico son más apropiadas que las mediciones de cero a pico, así como más precisas. Anota tus medidas en la gráfica (envía la gráfica anotada) y muestra tus cálculos con claridad. A partir de sus valores para\(f_d\) y\(\zeta\), calcule la frecuencia natural no amortiguada\(f_n\) (Hz). Para un sistema ligeramente amortiguado como este, ¿es la diferencia entre\(f_d\) y\(f_n\) numéricamente significativa, dada la precisión limitada de las cantidades medidas?

   

   Figura\(\PageIndex{2}\)

6. Un\(k\) sistema estándar\(m\) está inicialmente en reposo.\(c\) Entonces un ingeniero golpea la masa con un martillo de punta blanda que produce un pulso de fuerza de medio seno relativamente lento de amplitud 25 lb y duración 0.1 s [\(f_{x}(t)=25 \mathrm{lb} \times \sin (10 \pi t)\)para\(0 \leq t \leq 0.1\) s]. Tanto el pulso\(f_{x}(t)\) de fuerza como la respuesta\(x(t)\) de desplazamiento de la masa se registran en la gráfica siguiente. Para apoyar los cálculos asignados (página siguiente), anota tus mediciones en una fotocopia de la gráfica (mano en la gráfica anotada), y muestra tus cálculos claramente.
   1. Calcular a partir de la\(f_x(t)\) ecuación el impulso producido por la fuerza. Sin embargo, no debe usar esto\(I_F\) en la Ecuación 9.9.3 para determinar\(m\). Explique por qué no.
   2. Calcule a partir de la gráfica, con tanta precisión como lo permitan los datos, la frecuencia natural amortiguada\(f_d\) (Hz) y la relación\(\zeta\) de amortiguación viscosa del sistema.
   3. Se sabe que la masa del sistema\(m\) es de 0.0652 lb-s ² /inch. Calcular constante de rigidez\(k\) y constante de amortiguación\(c\).
7. Un gran sistema de amortiguador-resorte de masa (\(m\)\(c\)- -\(k\)) está inicialmente en reposo. Entonces una máquina impone sobre la masa una fuerza que varía lentamente en forma de pulso en diente de sierra de amplitud 800 N y duración de pulso 1.5 s,\(f_{x}(t)=\frac{800 \mathrm{N}}{1.5 \mathrm{s}} \times t\) para\(0 \leq t \leq 1.5\) s. Tanto el pulso\(f_{x}(t)\) de fuerza como la respuesta\(x(t)\) de desplazamiento de la masa se registran en la gráfica siguiente. Se emplea la inusual escala de desplazamiento “(mm * 100)” para acomodar los rangos de ambos\(f_{x}(t)\) y\(x(t)\) en la misma gráfica; esta escala simplemente significa que el rango de desplazamientos en la gráfica es\(-6.00 \mathrm{mm} \leq x(t) \leq+8.00 \mathrm{mm}\). Para apoyar los cálculos asignados (página siguiente), anota tus mediciones en una fotocopia de la gráfica (mano en la gráfica anotada), y muestra tus cálculos claramente.

   

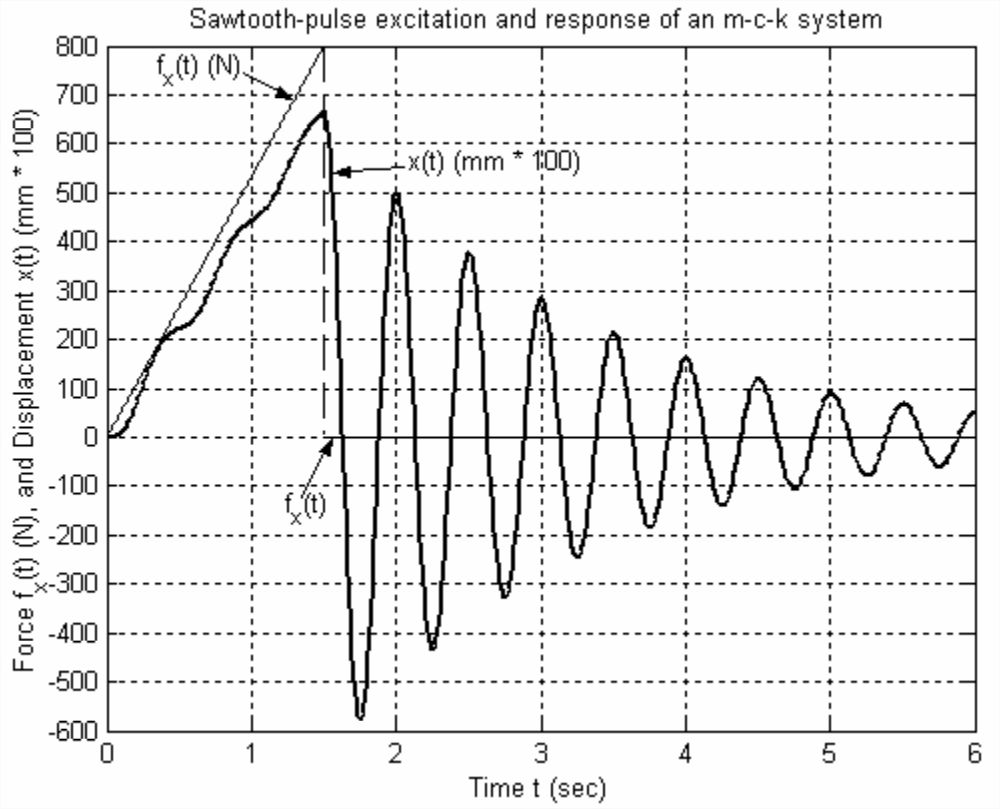
   Figura\(\PageIndex{3}\)

   1. Calcular el impulso total\(I_F\) producido por la fuerza. Sin embargo, no debe usar esto\(I_F\) en la Ecuación 9.9.3 para determinar\(m\). Explique por qué no.
   2. Calcule a partir de la gráfica, con tanta precisión como lo permitan los datos, la frecuencia natural amortiguada\(f_d\) (Hz) y la relación\(\zeta\) de amortiguación viscosa del sistema.
   3. La constante de rigidez del sistema\(k\) se sabe a partir de pruebas estáticas como 120.0 kN/m. Calcular la masa\(m\) y la constante de amortiguación\(c\).
   4. Encuentre la ecuación algebraica/numérica para la respuesta pseudo-estática\(x_{p s}(t)\) mientras el pulso está activo (\(0 \leq t \leq 1.5\)s), y compare su\(x_{p s}(t)\) con la respuesta real\(x(t)\) en la gráfica.
8. Considere el sistema de masa-amortiguador-muelle que se muestra en la siguiente figura, con: El sistema está inicialmente en reposo (la figura de la izquierda) en la posición de equilibrio estático para el peso\(m_{0} g\). A\(t\) = 0, la masa\(m_1\) se coloca suavemente\(m_0\) y luego se libera. Esto impone una fuerza de\(m_{1} g\) paso (el peso, debido a la gravedad) sobre el sistema. Tenga en cuenta también que la masa\(m_1\) cambia el sistema, ya que la masa vibratoria total ahora será\(m_{0}+m_{1}\), no solo\(m_{0}\). Use la Ecuación 9.6.5 para la respuesta de paso del sistema de ^segundo orden subamortiguada para escribir la ecuación numérica para la respuesta\(y(t)\) en pulgadas de masa combinada\(m_{0}+m_{1}\) (relativa a la posición de equilibrio estático para el peso de\(m_0\) solo, como se indica en el figura). Luego use MATLAB para trazar la curva de respuesta de\(y(t)\) versus\(t\) de\(t\) = 0 hasta que la masa se haya asentado dentro de al menos 2% de su posición final en estado estacionario. Esto significa trazar a al menos cuatro constantes de tiempo,\(t=4 \tau_{2}\), donde\(\tau_{2}=\left(\zeta \omega_{n}\right)^{-1}\). Dado que está multiplicando las funciones de tiempo sinusoidales por una función de tiempo exponencial, es necesario que utilice la multiplicación de matriz (.*) en MATLAB. Proporcione cuadrículas, títulos y etiquetas apropiados en su gráfica. No es necesario, pero puede verificar en su gráfica que la respuesta tiene los valores de frecuencia, desplazamiento en estado estacionario (estático final, pseudo-estático) y relación de amortiguación viscosa que puede calcular a partir de los datos originales para masa, amortiguación, rigidez y fuerza aplicada.

   

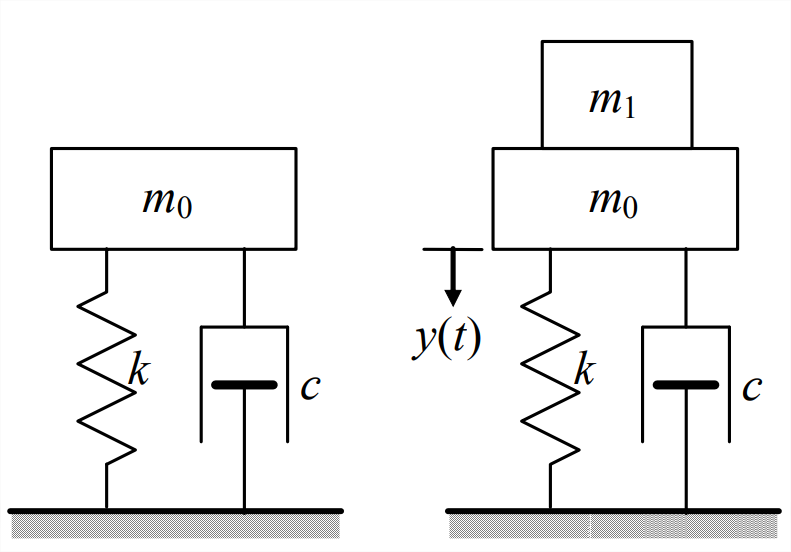
   Figura\(\PageIndex{4}\)

   1. \(m_0\)= 10.0 kg,\(c\) = 40.0 N-S/m,\(k\) = 400 N/m, y\(m_1\) = 2.00 kg;
   2. \(m_{0} g\)= 225 lb,\(c\) = 2.10 lb-s/pulgada,\(k\) = 30.5 lb/pulgada, y\(m_{1} g\) = 105 lb.
9. Para el\(k\) sistema\(m\) -\(c\) - y la entrada por escalonamiento/respuesta de la tarea Problema 9.8 [parte 9.8.1 o 9.8.2, lo que se asigne], utilice las ecuaciones de la Sección 9.8 para calcular el tiempo de subida\(t_r\), el tiempo pico\(t_p\), la relación\(\bar{y}_{p}\) máxima de sobreimpulso y el tiempo de asentamiento \(t_s\). Estos cálculos deben estar de acuerdo con los resultados comparables que puede medir a partir de su gráfica de respuesta escalonada de MATLAB para tarea Problema 9.8, asumiendo que su gráfica es correcta.
10. Peso\(W_{2}\) = 98.1 N (masa\(m_2\) = 10.0 kg) se suspende por una cuerda de peso\(W_1\) = 196.2 N (masa\(m_1\) = 20.0 kg), que se fija al techo por resorte\(k\) y amortiguador viscoso\(c\), como se muestra a continuación. El sistema está en equilibrio estático cuando, en el tiempo\(t\) = 0, la cuerda se corta limpiamente, cayendo\(W_{2}\). (Esto simula la liberación de una bomba desde un ala de avión flexible). Considerar la moción posterior\(x(t)\),\(t \geq 0\), de\(m_1\). Con el\(y(t)\) dato que se muestra en el dibujo, se puede pensar en esto como una respuesta escalonada, con la liberación de\(W_{2}\) ser equivalente a imponer sobre\(m_1\) una fuerza de paso ascendente igual a\(W_{2}\).

    

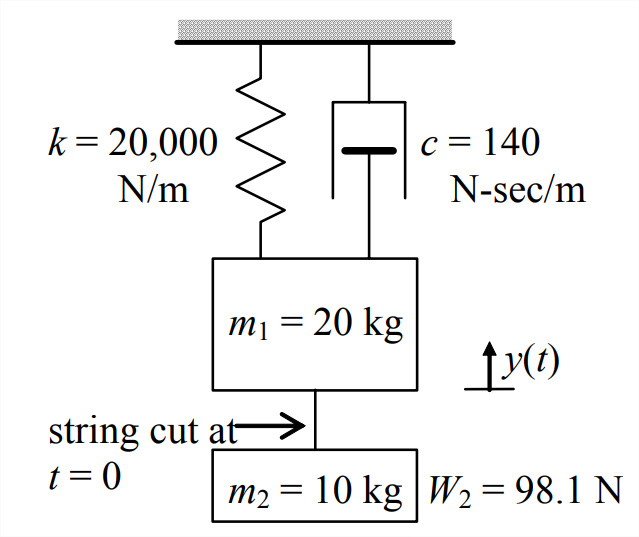
    Figura\(\PageIndex{5}\)

    1. Calcule la frecuencia natural no amortiguada\(f_n\) (Hz), la relación de amortiguación\(\zeta\), la frecuencia natural amortiguada\(f_d\) (Hz) y el período amortiguado de oscilación\(T_d\) (s).
    2. Calcular el valor estático final (as\(t \rightarrow \infty\))\(y\) y el tiempo de asentamiento\(t_s\) requerido para que el movimiento se asiente dentro del 2% de ese valor estático final.
    3. Dibuje una gráfica de la respuesta\(y(t)\) versus\(t\) desde\(t = 0\) hasta aproximadamente\(t = t_s\). No realice cálculos extensos; solo use los resultados de las partes 9.10.1 y 9.10.2 para dibujar el tipo de gráfico rápido de un ingeniero que muestre claramente las principales características de la respuesta, pero que no sea preciso como un gráfico generado por computadora.
11. Derivar la ecuación algebraica para respuesta escalonada\(x(t)\) con cero CI de sistemas de ^segundo orden amortiguados críticamente:\(\ddot{x}+2 \omega_{n} \dot{x}+\omega_{n}^{2} x=\omega_{n}^{2} U\), para\(t \geq 0\), con\(x(0)=0\) y\(\dot{x}(0)=0\). Un método fácil de solución, el enfoque convencional de la Sección 1.5, es usar solución homogénea Ecuación 9.1.11, agregarle una solución particular apropiada, luego hacer cumplir los CI para determinar las constantes desconocidas. (Respuesta:\(x(t)=U\left[1-\left(1+\omega_{n} t\right) e^{-\omega_{n} t}\right]\),\(t \geq 0\))
12. Habiendo resuelto por transformación de convolución inversa para respuestas escalonadas e impulsivas de sistemas de segundo orden subamortiguados, ahora podemos usar esos resultados para obtener con bastante facilidad dos pares de transformaciones de Laplace desordenadas. Utilice la Ecuación 9.3.5 primero con la Ecuación 9.6.5 y después con la Ecuación 9.7.3 para obtener\(f_{H}(t)=L^{-1}\left[\frac{\omega_{n}^{2}}{S\left[\left(s+\zeta \omega_{n}\right)^{2}+\omega_{d}^{2}\right]}\right]\) y\(f_{\delta}(t)=L^{-1}\left[\frac{\omega_{n}^{2}}{\left(s+\zeta \omega_{n}\right)^{2}+\omega_{d}^{2}}\right]\), tanto para\(0 \leq t\),\(|\zeta|<1\), y\(\omega_{d}^{2}>0\). Escribe las ecuaciones algebraicas para\(f_{H}(t)\) y\(f_{\delta}(t)\).
13. Considere el circuito LRC dibujado a continuación. El ODE que describe el voltaje de salida\(e_{o}(t)\) en términos de voltaje de entrada\(e_{i}(t)\) se deriva en el Ejemplo 9.2.1 de la Sección 9.2. Debido a que un inductor consiste principalmente en alambre enrollado, y debido a que el alambre enrollado acumula resistencia, un inductor real tiene resistencia así como inductancia. Un modelo de circuito común, simple y aproximado para tal inductor real es una combinación en serie de un inductor ideal y una resistencia,\(L\) y\(R_L\), como se muestra en el dibujo. Supongamos que un componente de circuito pequeño tiene los valores\(L\)\(R_L\) = 1.4 H y = 210\(\Omega\), y que está en serie con una capacitancia de\(C\) = 0.25\(\mu\) F (micro-faradios), como se muestra en el dibujo. Calcular la frecuencia natural\(f_n\) (Hz) y la relación\(\zeta\) de amortiguación de este circuito. Supongamos además que el voltaje de entrada es\(e_{i}(t)=1.50 H(t)\) voltios (una batería de 1.5 voltios se conecta repentinamente por interruptor\(S\)), y que todos los CI son cero (en particular, no hay carga inicial en el condensador). Utilice MATLAB para trazar la tensión de salida a\(e_{o}(t)\) lo largo de un intervalo de tiempo desde cero hasta que\(e_{o}(t)\) se asiente dentro de al menos 2% de su valor final de estado estacionario.
14. Se sabe que un dispositivo particular es un sistema de amortiguador-resorte de masa. Se requiere que la masa\(m\), la constante de amortiguación viscosa y la constante\(c\) de rigidez\(k\) se identifiquen experimentalmente a partir de una prueba de respuesta transitoria. En esta prueba, un ingeniero golpea bruscamente la masa con un martillo especialmente diseñado que está instrumentado con un sensor de fuerza. Se registra la entrada de fuerza a la masa, y el examen del historial de tiempo de fuerza real muestra que se aproxima estrechamente por un pulso de fuerza de medio seno particular que dura solo 20 milisegundos,\(f_{x}(t)=58.9 \sin 50 \pi t \times[H(t)-H(t-0.02 \mathrm{s})]\) lb La respuesta de desplazamiento medida de la masa se muestra en la gráfica a continuación. Utilice esta información para calcular\(m\)\(c\), y\(k\) en unidades consistentes y con tanta precisión como los datos lo permitan. Para apoyar estos cálculos, anota tus mediciones en la gráfica (mano en una fotocopia de la gráfica anotada), y muestra tus cálculos claramente. El pulso de fuerza de entrada es muy corto en relación con el período oscilatorio del sistema. Por lo tanto, para fines de identificación aproximada de parámetros, se debe asumir que la respuesta es muy cercana a la respuesta de impulso ideal del sistema a un impulso ideal\(f_{x}(t)=I_{F} \delta(t)\),, con\(I_F\) tener el valor del impulso del pulso real de fuerza de medio seno. [NOTA: después de calcular\(m\), y\(c\)\(k\), puede verificar fácilmente la validez de sus valores graficando (con MATLAB) la respuesta de impulso ideal de su sistema y luego comparando esa gráfica con el historial de tiempo real de respuesta. No obstante, esta comprobación es válida solo si usas el valor correcto de impulso\(I_F\), así que primero debes estar 100% seguro de que tu\(I_F\) es correcto.]

    

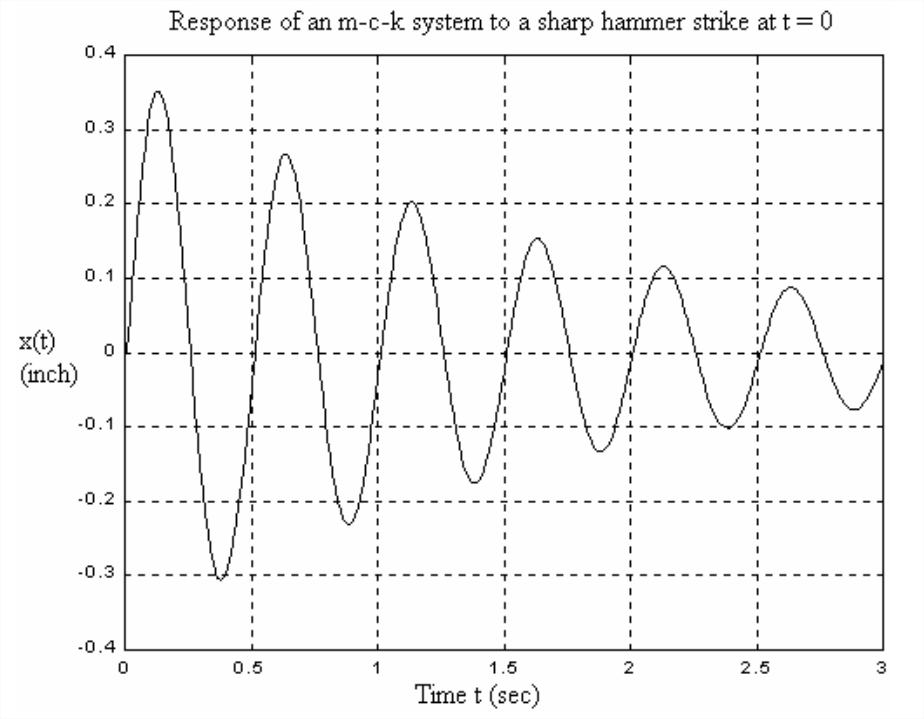
    Figura\(\PageIndex{6}\)

15. Para sistemas con el tipo particular de dinámica del lado derecho de la Ecuación 9.10.9, podemos definir una constante física\(T\) que tiene dimensiones de tiempo, luego escribir una forma modificada de la Ecuación ODE estándar 9.2.2 como\(\ddot{x}+2 \zeta \omega_{n} \dot{x}+\omega_{n}^{2} x=\omega_{n}^{2} T \dot{u}(t)\). [Se puede verificar fácilmente, por ejemplo, que\(T=\tau_{H}\) para el filtro paso banda, Ecuación 9.10.9.] La respuesta CI pura de esta ecuación es la misma que la de las Ecuaciones 9.4.1 y 9.4.2, así que centrémonos en la respuesta forzada y fijemos todos los CI = 0. También, supongamos inicialmente eso\(|\zeta|<1\), así que\(\omega_{d}^{2}=\omega_{n}^{2}\left(1-\zeta^{2}\right)>0\)).
    1. Para esta ODE modificada, siga los pasos de las Ecuaciones 9.3.2 a 9.3.5, y asuma también eso\(u(0)=0\). para encontrar\(L[x(t)]=\frac{\omega_{n}^{2} T}{\omega_{d}} \frac{s \omega_{d}}{\left(s+\zeta \omega_{n}\right)^{2}+\omega_{d}^{2}} L[u(t)]\). A continuación, utilice un par de transformaciones de Laplace desarrollado, en efecto, entre las Ecuaciones 9.3.5 y 9.3.9 para resolver\(x(t)\) si la entrada es la función de paso\(u(t)=U H(t)\). ¿Cuál de los cero CI se conserva o no en esta solución?
    2. Utilice la transformada inversa para la respuesta escalonada de la parte 9.15.1, y la transformada general\(L[\dot{f}(t)]=s F(s)-f(0)\) para derivar la siguiente transformada inversa:\[L^{-1}\left[\frac{s \omega_{d}}{\left(s+\zeta \omega_{n}\right)^{2}+\omega_{d}^{2}}\right]=e^{-\zeta \omega_{n} t}\left(\omega_{d} \cos \omega_{d} t-\zeta \omega_{n} \sin \omega_{d} t\right) \nonumber \]
    3. Utilice el resultado de la parte 9.15.2 y la transformación de convolución inversa para escribir\(\left.x(t)\right|_{I C s=0}\) ecuaciones, que involucran integrales de convolución, que aplican para la función de entrada arbitraria\(u(t)\).
    4. Utilice el resultado de la parte 9.15.2 y la Ecuación 8.6.6 para mostrar que la ecuación algebraica para la función unidad-impulso-respuesta (IRF) válida para la ODE de ^segundo orden modificada con dinámica del lado derecho es\(h(t)=\omega_{n}^{2} T e^{-\zeta \omega_{n} t}\left[\cos \omega_{d} t-\left(\zeta \omega_{n} / \omega_{d}\right) \sin \omega_{d} t\right]\). Ahora usa esta IRF para escribir una ecuación integral de Duhamel, Ecuación 8.7.2, para\(\left.x(t)\right|_{I C s=0}\) eso se aplica para la función de entrada arbitraria\(u(t)\).
    5. Los resultados de las partes 9.15.1-9.15.4 aplican para un sistema de ^segundo orden subamortiguado,\(|\zeta|<1\). Pero el Ejemplo 9.10.1 en la Sección 9.10 muestra que un filtro de paso de banda RC, para uno, es un sistema de orden ^2º sobreamortiguado, por lo que necesitamos convertir los resultados anteriores para obtener resultados válidos para\(|\zeta|>1\). Utilice los métodos de la Sección 9.10 para escribir una ecuación algebraica para IRF\(h(t)\) y una ecuación integral para\(\left.x(t)\right|_{I C s=0}\), ambas válidas para la ODE de segundo orden ^{sobreamortiguada} modificada con dinámica del lado derecho y esta última válida para la función de entrada arbitraria\(u(t)\).
16. La Figura 9.7 incluye una curva que es la respuesta escalonada de un sistema estándar sobre amortiguado ^{de segundo} orden. Utilice los métodos de la Sección 9.10 para derivar la ecuación algebraica a partir de la cual se calculó esa curva en particular. Respuesta:\[x(t)=U\left[1-e^{-\zeta \omega_{n} t}\left(\cosh \mu_{d} t+\frac{\zeta \omega_{n}}{\mu_{d}} \sinh \mu_{d} t\right)\right], \text { for } 0 \leq t \text { and } \zeta>1, \mu_{d} \equiv \omega_{n} \sqrt{\zeta^{2}-1} \nonumber \]
17. El circuito dibujado a la derecha ² consta de tres etapas, cada una construida alrededor de un amplificador operacional, y hay retroalimentación de voltaje\(e_{f}(t)\) desde la última etapa (derecha) hasta la primera etapa (izquierda), donde\(e_{i}(t)\) se aplica el voltaje de entrada. El voltaje de salida del circuito\(e_{o}(t)\),, es la salida de la etapa media. La primera etapa es un integrador sumador e inversor; utilizar los métodos del Capítulo 5 para derivar la primera ODE,\(e_{m} / R_{c}+e_{f} / R_{b}+e_{i} / R_{a}=-C \dot{e}_{m}\). A continuación, para la etapa media, un integrador inversor, deriva la segunda ODE,\(e_{m} / R_{b}=-C \dot{e}_{o}\) (tarea Problema 5.6); ahora usa la segunda ODE para sustituir\(e_{m}\) en la primera ODE, y diferenciar la segunda ODE y usar el resultado para sustituir\(\dot{e}_{m}\) en la primera ODE. La última etapa del circuito es un inversor de signo simple, para lo cual\(e_{f}=-e_{o}\) a partir de la Ecuación 5.3.5; sustituir\(e_{f}\) y mostrar que la ODE que relaciona la tensión de salida con la tensión de entrada\(e_{o}(t)\)\(e_{i}(t)\) para todo el circuito es\(\ddot{e}_{o}+\frac{1}{R_{c} C} \dot{e}_{o}+\left(\frac{1}{R_{b} C}\right)^{2} e_{o}=\left(\frac{1}{R_{b} C}\right)^{2} \frac{R_{b}}{R_{a}} e_{i}\). Convierta esta ODE en la forma de orden 2 ^nd amortiguada estándar Ecuación 9.2.2,\(\ddot{e}_{o}+2 \zeta \omega_{n} \dot{e}_{o}+\omega_{n}^{2} e_{o}=\omega_{n}^{2} u(t)\); escriba ecuaciones específicas (en términos de las resistencias, capacitancias y voltaje de entrada de este circuito) para frecuencia natural no amortiguada\(\omega_{n}\)\(\zeta\), relación de amortiguación viscosa y cantidad de entrada\(u(t)\).
18. El giroscopio de una velocidad (Ejemplo 9.2 en la Sección 9.2) tiene los siguientes parámetros del rotor: inercia\(J_{r}=2.9 \times 10^{-4} \mathrm{kg}-\mathrm{m}^{2}\) rotacional polar y\(\Omega_{r}=2,100\) revoluciones de velocidad de giro por minuto (rpm); además, tiene los siguientes parámetros del eje cardán: inercia rotacional polar\(J_{\theta}=2.2 \times 10^{-4} \mathrm{kg}-\mathrm{m}^{2}\)\(J_{\theta}=2.2 \times 10^{-4} \mathrm{kg}-\mathrm{m}^{2}\), y amortiguación constante\(c_{\theta}=0.0046 \mathrm{N}-\mathrm{m} /(\mathrm{rad} / \mathrm{s})\) y constante de rigidez\(k_{\theta}=0.096 \mathrm{N}-\mathrm{m} / \mathrm{rad}\). Considere la rotación del eje cardán de salida\(\theta(t)\) en respuesta a una velocidad de rotación del plato giratorio de entrada que se aproxima a la función de paso\(p(t) \approx P \times H(t)\). (Solo un momento de impulso ideal físicamente imposible que actúe sobre el plato giratorio podría producir un cambio de paso exacto en la velocidad de rotación; por lo tanto, imagine para este problema que un pulso de momento muy corto pero muy grande produce la función de paso aproximado, pero use las ecuaciones que aplican para una exacta función de paso.) Para los\(P=15\) grados/s de magnitud escalonada, calcule las siguientes cantidades de respuesta: rotación pseudo-estática del eje cardán,\(\theta_{p s}\) (en grados); y tiempo de subida,\(t_{r}\); y tiempo pico,\(t_p\); y relación máxima de sobreimpulso,\(\bar{x}_{p}\). (Respuesta parcial:\(t_{p}=0.174\) s) La teoría desarrollada en el Ejemplo 9.2.2 es precisa solo si la rotación del cardán\(\theta (t)\) es suficientemente pequeña que\(\cos \theta(t) \approx 1\), digamos,\(\cos \theta(t)>0.95\). Para los parámetros en este problema, ¿se cumple este criterio de precisión?
19. Otro tipo de sensor giroscópico de un solo eje es similar al giroscopio de velocidad descrito en el Ejemplo 9.2.2 de la Sección 9.2 excepto que no hay resorte para limitar la rotación del conjunto cardán-eje, por lo que\(k_{\theta}=0\) en las ecuaciones derivadas en el Ejemplo 9.2.2. Por lo tanto, la ecuación de movimiento se convierte efectivamente en ^una ODE de primer orden en variable dependiente\(\dot{\theta}(t)\), la tasa de rotación del eje cardán:\[J_{\theta} \ddot{\theta}+c_{\theta} \dot{\theta}=J_{r} \Omega_{r} p(t) \nonumber \] Observe desde la ODE que es la respuesta pseudo-estática\((\dot{\theta})_{p s}=\left(J_{r} \Omega_{r} / c_{\theta}\right) p(t)\). Pero el transductor eléctrico de este dispositivo detecta\(\theta(t)\), no\(\dot{\theta}(t)\), lo que significa que la cantidad percibida tiene la forma\(\theta(t)=\int_{t} \dot{\theta}(\tau) d \tau=\left(J_{r} \Omega_{r} / c_{\theta}\right) \int_{t} p(\tau) d \tau\). Por lo tanto, este tipo de sensor se denomina giroscopio de integración de velocidad; su salida es proporcional, no a la velocidad de rotación, sino al ángulo de rotación real del plato giratorio,\(\psi(t)=\int_{t} p(\tau) d \tau\), donde\(p \equiv \dot{\psi}\). Considere la velocidad de rotación del eje cardán de salida\(\dot{\theta}(t)\) y la rotación\(\theta(t)\) en respuesta a una velocidad de rotación de la plataforma giratoria de entrada que se aproxima al siguiente pulso plano de duración\(t_{d}\):\ [p (t) =\ left\ {\ begin {array} {l}
    0,\ quad t<0 \\
    P, 0<t<t_ {d}\ quad,\ text {en que magnitud} P\ text {es constante}\\
    0,\ quad t_ {d} <t
    \ end {array}\ right. \ nonumber\] (Solo los momentos de impulso ideales físicamente imposibles que actúan sobre el plato giratorio podrían producir cambios de paso exactos en la velocidad de rotación; por lo tanto, imagine para este problema que pulsos de momento muy cortos pero muy grandes produzcan los cambios de paso aproximados, pero use las ecuaciones que se aplican para el pulso plano exacto.)
    1. La solución matemática para la respuesta de un sistema estable estándar ^de primer orden a una entrada de pulso plano se da en la tarea Problema 6.2.1. Adapte esta solución para escribir ecuaciones de respuesta para la tasa de rotación del eje cardán del giroscopio integrador de velocidad\(\dot{\theta}(t)\), dado el IC\(\dot{\theta}(0)=0\). A continuación, integre apropiadamente (¡muestre todos los detalles!) las\(\dot{\theta}(t)\) ecuaciones, dado el IC\(\theta(0)=0\), para derivar las siguientes ecuaciones para la rotación del eje cardán:\ [\ theta (t) =\ left\ {\ begin {aligned}
       b P\ tau_ {1}\ left [t-\ tau_ {1}\ left (1-e^ {-t/\ tau_ {1}}\ right)\ right], & 0\ leq t\ leq t_ {d}\\
       \ theta\ izquierda (t_ {d}\ derecha) +b P\ tau_ {1} ^ {2}\ izquierda (1-e^ {-t_ {d}/\ tau_ {1}}\ derecha)\ izquierda (1-e^ {-\ izquierda (t-t_ {d}\ derecha)/\ tau_ {1}}\ derecha), & t_ {d}\ leq t
       \ end {alineado}\ derecho. \ nonumber\] donde\(b=J_{r} \Omega_{r} / J_{\theta}\) y\(\tau_{1}=J_{\theta} / c_{\theta}\).
    2. Un giroscopio integrador de velocidad tiene los siguientes parámetros del rotor: inercia\(J_{r}=2.9 \times 10^{-4} \mathrm{kg}-\mathrm{m}^{2}\) rotacional polar y\(\Omega_{r}=420\) revoluciones por minuto (rpm); además, tiene los siguientes parámetros del eje cardán: inercia\(J_{\theta}=8.5 \times 10^{-4} \mathrm{kg}-\mathrm{m}^{2}\) rotacional polar y constante de amortiguación\(c_{\theta}=9.2 \times 10^{-3}\) N-m/ (rad/s). Para los\(P=5\) grados de magnitud de tasa de rotación de pulso plano y la duración del pulso\(t_{d}=2.5\) s, calcule y grafique a partir de las ecuaciones de la parte 9.19.1 la rotación del eje cardánico\(\theta(t)\) (en grados) durante el intervalo de tiempo\(0 \leq t \leq 5\). La teoría desarrollada en el Ejemplo 9-2 es precisa solo si la rotación del eje cardán\(\theta(t)\) es suficientemente pequeña que\(\cos \theta(t) \approx 1\), digamos,\(\cos \theta(t)>0.95\). Para los parámetros en este problema, ¿se cumple este criterio de precisión?
    3. Ya que\((\dot{\theta})_{p s}=\left(J_{r} \Omega_{r} / c_{\theta}\right) p(t)=\left(J_{r} \Omega_{r} / c_{\theta}\right) \dot{\psi}(t)\), es evidente que la salida del giroscopio integrador de velocidad está diseñada para ser proporcional, tan cerca como su dinámica lo permita, al ángulo de rotación real del plato giratorio, es decir,\(\theta(t) \approx\left(J_{r} \Omega_{r} / c_{\theta}\right) \psi(t)\); por lo tanto, la ecuación que estima\(\psi(t)\) a partir de la rotación medida del eje cardán es \(\psi(t) \approx\left[c_{\theta} /\left(J_{r} \Omega_{r}\right)\right] \theta(t)\). Utilice su calculado a\(\theta(t)\) partir de la parte 9.19.2 para calcular y trazar la cantidad\(\left[c_{\theta} /\left(J_{r} \Omega_{r}\right)\right] \theta(t)\) en el mismo intervalo de tiempo,\(0 \leq t \leq 5\) s. a continuación, calcule el ángulo de rotación real de la plataforma giratoria desde\(\psi(t)=\int_{0}^{t} p(\tau) d \tau\), dado el IC\(\psi(0)=0\), y graficarlo en la misma gráfica para su comparación con\(\left[c_{\theta} /\left(J_{r} \Omega_{r}\right)\right] \theta(t)\). En este caso, ¿qué tan bien sigue el giroscopio integrador de velocidad la rotación real del plato giratorio?

¹ La excitación de la base es la entrada de desplazamiento impuesta en el lado “tierra” o “base” del resorte en lugar de directamente sobre la masa. Es muy común considerar la excitación de base en los análisis de la respuesta inducida por terremotos de edificios, llantas de automóviles rodando sobre carreteras con baches y aislamiento de vibraciones de dispositivos sensibles como cargas útiles delicadas en propulsores de cohetes.

² Este circuito es esencialmente la computadora analógica electrónica (ver la nota al pie de la tarea Problema 5.6) para resolver la ecuación ODE 9.2.2.