10.1: Respuesta de frecuencia de sistemas de segundo orden sin amortiguar y resonancia

Como se discutió en la Sección 7.1, un sistema pasivo de ^segundo orden verdaderamente sin amortiguar es físicamente poco realista. Sin embargo, es útil derivar la respuesta de frecuencia para este tipo ideal de sistema, ya que los resultados revelan características importantes del comportamiento resonante de los sistemas generales de ^segundo orden subamortiguados. Además, la respuesta de frecuencia de un sistema de ^segundo orden no amortiguado es, para muchos propósitos prácticos, una aproximación de ingeniería simple pero satisfactoria a la respuesta de frecuencia del sistema de ^segundo orden ligeramente amortiguado correspondiente.

Considere la ODE estándar para sistemas idealizados de ^segundo orden sin amortiguar:

\[\ddot{x}+\omega_{n}^{2} x=\omega_{n}^{2} u(t)\label{eqn:10.1} \]

Para derivar respuesta de frecuencia, dejamos\(u(t)=U \cos \omega t\) y buscamos la respuesta sinusoidal en estado estacionario en la forma\(x(t)=X_{S}(\omega) \cos \omega t\), en la que\(X_{S}(\omega)\) se encuentra la cantidad desconocida. Encontramos una ecuación para\(X_{S}(\omega)\) sustituyendo en Ecuación\(\ref{eqn:10.1}\):

\[\left(-\omega^{2}+\omega_{n}^{2}\right) X_{S}(\omega) \cos \omega t=\omega_{n}^{2} U \cos \omega t \nonumber \]

\[\Rightarrow \frac{X_{S}(\omega)}{U}=\frac{\omega_{n}^{2}}{\omega_{n}^{2}-\omega^{2}}=\frac{1}{1-\left(\omega / \omega_{n}\right)^{2}}\label{eqn:10.2} \]

Nota de la Ecuación\(\ref{eqn:10.2}\) que\(X_{S}(\omega)\) es una cantidad con signo; puede ser positiva o negativa dependiendo del valor de la relación de frecuencia\(\omega / \omega_{n}\) relativa a 1. Pero nuestra notación convencional para una función de respuesta de frecuencia es\(F R F(\omega)=\frac{X(\omega)}{U} e^{j \phi(\omega)}\), Ecuación 7.7.18, en qué magnitud\(X(\omega) \geq 0\). Por lo tanto, inferimos de\(\ref{eqn:10.2}\) la Ecuación las siguientes funciones de relación de magnitud y fase en la notación convencional:

\ [\ frac {X (\ omega)} {U} =\ izquierda|\ frac {1} {1-\ izquierda (\ omega/\ omega_ {n}\ derecha) ^ {2}}\ derecha|,\ phi (\ omega) =\ izquierda\ {\ begin {array} {r}
0^ {\ circ}\ text {para} 0\ leq\ omega/omega/ a_ {n} <1\\
-180^ {\ circ}\ text {for} 1<\ omega/\ omega_ {n}
\ end {array}\ right. \ label {eqn:10.3}\]

Las ecuaciones\(\ref{eqn:10.3}\) dan la función de respuesta de frecuencia (FRF) de un sistema de ^segundo orden no amortiguado. La relación de magnitud\(X(\omega) / U\) y fase\(\phi(\omega)\) se representan en la Figura\(\PageIndex{1}\) como funciones de la relación de frecuencia de excitación\(\omega / \omega_{n}\).

La característica más importante de las ecuaciones FRF\(\ref{eqn:10.3}\) es la magnitud infinita de la respuesta de estado estacionario cuando la frecuencia de excitación es\(\omega\) exactamente igual a la frecuencia natural\(\omega_n\). Esta es la versión extrema del fenómeno llamado resonancia. En realidad, cualquier amortiguación, por pequeña que sea, reduce la magnitud de resonancia infinita de la Fig. 10-1 a algún valor finito, como se demuestra en la siguiente sección; pero ese valor finito seguirá siendo generalmente mucho mayor que la respuesta estática o pseudo-estática, que es\(X(\omega \approx 0)=U\). La figura\(\PageIndex{1}\) muestra también que la magnitud de respuesta se amplifica en gran medida con respecto a la respuesta estática incluso si la frecuencia de excitación es cercana (pero no igual) a la frecuencia natural; nótese, por ejemplo, que la amplificación dinámica supera cinco (5) siempre que la frecuencia de excitación\(\omega\) está dentro de aproximadamente el\(\pm\) 10% de la frecuencia natural\(\omega_n\). Esta alta sensibilidad a la excitación cerca de la frecuencia natural es una característica muy importante de los sistemas de ^segundo orden ligeramente amortiguados. Hay discusión adicional de resonancia en la siguiente sección.

Figura\(\PageIndex{1}\): Función de respuesta de frecuencia de un sistema de ^{segundo orden no} amortiguado

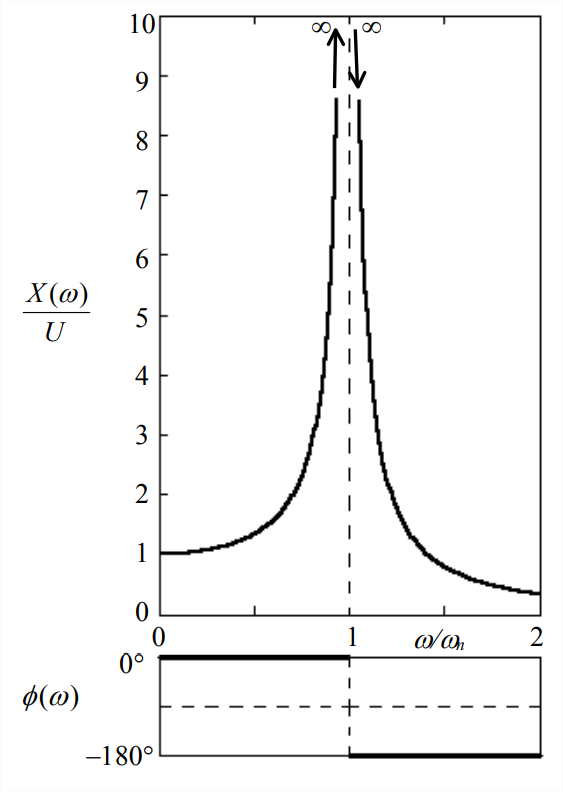
Las ecuaciones FRF\(\ref{eqn:10.3}\) contienen no solo la magnitud sino también la fase\(\phi\): para\(\omega<\omega_{n}\), la fase es 0°, por lo que la respuesta está exactamente en fase con la excitación; sin embargo, para\(\omega>\omega_{n}\), la fase es −180°, por lo que la respuesta está exactamente desfasada con la excitación.