10.2: Respuesta de frecuencia de sistemas amortiguados de segundo orden

De la Sección 9.2, la forma estándar de la ODE de ^segundo orden es:

\[\ddot{x}+2 \zeta \omega_{n} \dot{x}+\omega_{n}^{2} x=\omega_{n}^{2} u(t) \label{eqn:10.4} \]

Para derivar respuesta de frecuencia, tomamos la transformada de Laplace de Ecuación\(\ref{eqn:10.4}\), con cero IC:

\[\left.\left(s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}\right) L[x(t)]\right|_{I C s=0}=\omega_{n}^{2} L[u(t)]\label{eqn:10.5} \]

Definición La ecuación 4.6.3 para la función de transferencia da

\[T F(s)=\frac{\left.L[x(t)]\right|_{I C s=0}}{L[u(t)]}=\frac{\omega_{n}^{2}}{s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}}\label{eqn:10.6} \]

Entonces la relación fundamental Ecuación 4.7.18 entre la función de transferencia y la función de respuesta de frecuencia compleja da

\[F R F(\omega)=T F(j \omega)=\frac{\omega_{n}^{2}}{-\omega^{2}+j 2 \zeta \omega_{n} \omega+\omega_{n}^{2}}=\frac{1}{\left(1-\omega^{2} / \omega_{n}^{2}\right)+j 2 \zeta \omega / \omega_{n}}\label{eqn:10.7} \]

Para simplificar la notación, definimos la relación de frecuencia de excitación adimensional, la frecuencia de excitación relativa a la frecuencia natural no amortiguada del sistema:

\[\beta \equiv \frac{\omega}{\omega_{n}}\label{eqn:10.8} \]

Con notación Ecuación\(\ref{eqn:10.8}\), la relación Ecuación 4.7.18 entre\(F R F(\omega)\) y la relación de magnitud\(X(\omega) / U\) y ángulo\(\phi(\omega)\) de fase de la respuesta de frecuencia da

\[F R F(\omega)=\frac{1}{\left(1-\beta^{2}\right)+j 2 \zeta \beta}=\frac{X(\omega)}{U} e^{j \phi(\omega)}\label{eqn:10.9} \]

Después de la manipulación estándar de la fracción compleja en Ecuación\(\ref{eqn:10.9}\), encontramos las siguientes ecuaciones para relación de magnitud y ángulo de fase [tarea Problema 2.6.1]:

\[\frac{X(\omega)}{U}=\frac{1}{\sqrt{\left(1-\beta^{2}\right)^{2}+(2 \zeta \beta)^{2}}}, \quad \phi(\omega)=\tan ^{-1}\left(\frac{-2 \zeta \beta}{1-\beta^{2}}\right), \quad \beta \equiv \frac{\omega}{\omega_{n}}\label{eqn:10.10} \]

Tenga en cuenta que los resultados\(\ref{eqn:10.10}\) Las ecuaciones son válidas para cualquier valor no negativo de la relación de amortiguación viscosa\(\zeta \geq 0\); a diferencia de la mayoría de las ecuaciones de tiempo-respuesta derivadas en el Capítulo 9, las ecuaciones por\(\ref{eqn:10.10}\) sí solas se aplican para sistemas de ^segundo orden subamortiguados, amortiguados críticamente y sobreamortiguados.

Resultados Las ecuaciones\(\ref{eqn:10.10}\) se representan en la Figura\(\PageIndex{1}\) para relaciones de amortiguamiento viscoso que varían de 0 a 1. Las gráficas de la Figura\(\PageIndex{1}\) se produjeron con el uso de MATLAB (Versión 6 o posterior). Primero, se programó un archivo M para calcular y graficar FRF usando el método descrito en la declaración de tarea Problema 4.3 [comenzando con la ecuación FRF compleja\(\ref{eqn:10.9}\)), no las ecuaciones reales Ecuaciones\(\ref{eqn:10.10}\)]:

%frf2orddamped.m

%Fig. 10-2 Respuesta de frecuencia, amortiguado de 2do orden

% Relación de magnitud para amortiguación cero, zeta=0

bt0a=logspace (-1, log10 (0.998) ,100);

frf0a =( 1) ./ (1-bt0a.^2);

loglog (bt0a, frf0a, 'k'), espera

bt0b=logspace (log10 (1.002) ,1100);

frf0b =( 1). /(bt0b.^2-1);

loglog (bt0b, frf0b, 'k')

% Relación de magnitud para varios casos de zeta > 0

bt1=logspace (-1,1,400);

zt= [0.05 0.1 0.2 0.5 1/sqrt (2) 1]; nzts=longitud (zt);

para i=1:nzts

frf =( 1) ./ (1-bt1.^2+j*2*zt (i). *bt1);

magrat=abs (frf);

loglog (bt1, magrat, 'k')

final

retener

% Ángulo de fase en grados para amortiguación cero, zeta=0

bt0a= [0.1 1]; faz0a=ceros (1,2);

figura, semilogx (bt0a, faz0a, 'k'), espera

bt0b= [1 10]; faz0b=-180*unos (1,2);

semilogx (bt0b, faz0b, 'k')

% Ángulo de fase en grados para varios casos de zeta > 0

para i=1:nzts

frf =( 1) ./ (1-bt1.^2+j*2*zt (i). *bt1);

faz=ángulo (frf) *180/pi;

semilogx (bt1, faz, 'k')

final

Después de ejecutar el archivo M, se utilizaron las extensas funciones de edición de figuras de MATLAB para establecer límites de ejes y generar títulos, etiquetas y anotaciones de curvas.

A pesar de\(\PageIndex{1}\) que la Figura fue producida por gráficos asistidos por computadora, sigue siendo importante que entiendas cómo evaluar Ecuaciones\(\ref{eqn:10.10}\) con una calculadora manual. Estas ecuaciones parecen simples, pero pueden ser complicadas, particularmente para el caso especial\(\zeta=0\). Ver tarea Problema 2.6.2 para obtener ayuda con la comprensión de cómo evaluar ecuaciones\(\ref{eqn:10.10}\) numéricamente.

Hay varias características notables de la respuesta de frecuencia de los sistemas amortiguados de ^segundo orden, a partir de Ecuaciones\(\ref{eqn:10.10}\) y Figura\(\PageIndex{1}\):

• Resonancia: relación de magnitud máxima (pico) La frecuencia a la que se produce la relación de magnitud pico se denomina frecuencia de resonancia, denotada\(\omega_{r}\), y esta frecuencia es menor que la frecuencia natural\(\omega_{n}\) si la amortiguación es positiva,\(\zeta>0\). Para encontrar el máximo, diferenciamos la relación de magnitud de las Ecuaciones\(\ref{eqn:10.10}\), establecemos el resultado a cero y resolvemos para la frecuencia asociada (puedes verificar el resultado tú mismo, o ver Meirovitch, 2001, pp. 115-116 para los detalles de cálculo y álgebra; además, existen enfoques alternativos instructivos en Ogata, 1998, pp. 480-481 y en Clark, 1962, pp. 316-322): El \[\frac{d}{d \beta}\left(\frac{X(\beta)}{U}\right)=0 \Rightarrow \beta_{r}=\sqrt{1-2 \zeta^{2}} \Rightarrow \omega_{r}=\omega_{n} \sqrt{1-2 \zeta^{2}}\label{eqn:10.11} \]subíndice\(r\) en la ecuación\(\ref{eqn:10.11}\) denota una cantidad de resonancia correspondiente a la relación de magnitud pico\(X_{r} / U\). La frecuencia de excitación debe ser real y mayor o igual a cero, por lo que\(\omega_{r}=\omega_{n} \sqrt{1-2 \zeta^{2}}\) es válida sólo para\(0 \leq \zeta \leq 1 / \sqrt{2}=0.707\). Si\(\zeta\) es positivo pero muy pequeño, entonces\(X_{r} / U\) ocurre casi a la frecuencia natural,\(\omega_{r} \approx \omega_{n}\). A\(\zeta\) medida que aumenta desde valores positivos muy pequeños,\(\omega_{r}\) disminuye hasta, para\(\zeta=1 / \sqrt{2}\),\(\omega_{r}=0\). Sin embargo, la amplificación dinámica es insignificante para valores\(\zeta\) mayores de aproximadamente 0.5. Sustituyendo la Ecuación\(X(\omega) / U\) de\(\ref{eqn:10.11}\) nuevo en Ecuaciones\(\ref{eqn:10.10}\) da (después de más álgebra) el valor de resonancia: \[\frac{X\left(\beta_{r}\right)}{U}=\frac{X_{r}}{U}=\frac{1}{2 \zeta \sqrt{1-\zeta^{2}}}\label{eqn:10.12} \]Nota de la Ecuación\(\ref{eqn:10.12}\) que para\(\zeta=1 / \sqrt{2}\) [el valor máximo permisible para la validez de la Ecuación\(\ref{eqn:10.11}\)], tenemos\(X_{r} / U=1\) en \(\omega_{r}=0\). Como lo indica la tendencia en la Figura\(\PageIndex{1}\), para mayores relaciones de amortiguación,\(\zeta \geq 1 / \sqrt{2}\), la magnitud\(X(\omega) / U\) es máxima en\(\omega=0\), y disminuye monótonamente a medida que\(\omega\) aumenta.

  

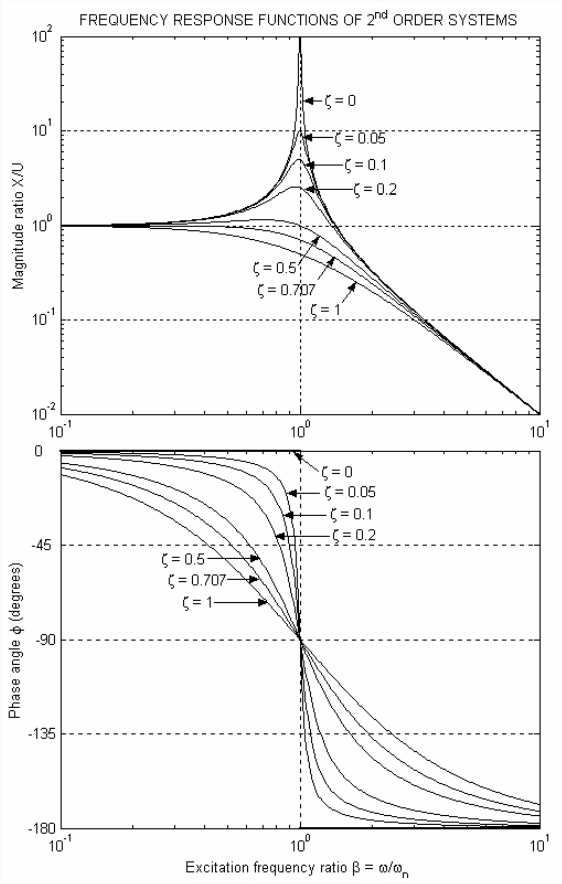
  Figura\(\PageIndex{1}\): Funciones de respuesta de frecuencia para sistemas estándar ^{de segundo} orden con relaciones de amortiguación viscosas que\(\zeta\) varían de 0 a 1

• Respuesta a la frecuencia natural La respuesta de frecuencia a\(\omega=\omega_{n}\),\(\beta=1\), consiste en ángulo de fase\(\phi\left(\omega_{n}\right)=-90^{\circ}\) independientemente del valor de la relación de amortiguación viscosa\(\zeta\), y la relación de magnitud\(X\left(\omega_{n}\right) / U=1 /(2 \zeta)\). Además, la respuesta de magnitud pico se produce esencialmente en\(\omega=\omega_{n}\) si la amortiguación es pequeña, como se analiza a continuación.
• Amortiguación viscosa pequeña, pequeña\(\zeta\) aproximación Si la amortiguación es tan pequeña que\(\sqrt{1-2 \zeta^{2}}\approx 1\), entonces podemos usar las siguientes aproximaciones precisas de los valores asociados a la respuesta en resonancia, de Ecuaciones\(\ref{eqn:10.11}\) y\(\ref{eqn:10.12}\): \[\omega_{r}=\omega_{n} \sqrt{1-2 \zeta^{2}} \approx \omega_{n}\label{eqn:10.13} \] \[\frac{X_{r}}{U}=\frac{1}{2 \zeta \sqrt{1-\zeta^{2}}} \approx \frac{X\left(\omega_{n}\right)}{U}=\frac{1}{2 \zeta}\label{eqn:10.14} \]Se trata del límite superior de la relación de amortiguamiento viscoso para el que la pequeña\(\zeta\) aproximación es prácticamente útil\(\zeta=0.2\), que podemos ver en la Figura\(\PageIndex{1}\). En este límite superior, la aproximación está en error del orden del 4%, ya que\(\sqrt{1-2(0.2)^{2}}=0.959\). La ecuación del factor de amplificación de\(\zeta\) resonancia pequeña a veces\(\ref{eqn:10.14}\) se denomina factor de calidad, y se denota\(Q=1 /(2 \zeta)\). La referencia de “calidad” es a la sintonización, especialmente de un dispositivo receptor como una radio (Hammond, 1961, pp. 106-114). Cuando giras el dial de sintonización analógica de una radio antigua, estás variando el valor de la capacitancia en un circuito de sintonización\(LRC\) eléctrica para producir resonancia con la señal portadora electromagnética, lo que da la recepción más fuerte posible. Claramente,\(Q\) es deseable un alto en el circuito de sintonización de una radio. Por otro lado, el alto\(Q\) suele ser indeseable en los sistemas mecánicos, ya que puede llevar a fallas estructurales u otras consecuencias negativas. Por ejemplo, si el sistema que consiste en la llanta de un automóvil, el resorte de suspensión y el puntal de amortiguación resuena con las olas en un camino de tierra de tabla de lavar, entonces la vibración resultante producirá una mala calidad de conducción e incluso podría romper las piezas del automóvil.

  Observe en el\(\PageIndex{1}\) gráfico de la Figura de relación de magnitud que la\(\zeta=0\) curva limita las curvas para todos\(\zeta>0\), y que proporciona una buena aproximación para pequeñas\(\zeta\) en todas las frecuencias excepto las cercanas\(\omega_{n}\); para amortiguamiento pequeño, por lo tanto, la ecuación simple (10-3a) para magnitud será, para algunos cálculos, suficientemente precisa.

• Ángulos de fase de respuesta de frecuencia La figura\(\PageIndex{1}\) muestra que cuanto más ligeramente amortiguado esté un sistema, más cerca está su respuesta de estar en fase con excitación por debajo de la frecuencia natural, y fuera de fase con excitación por encima de la frecuencia natural. Además, para la excitación a la frecuencia natural,\(\omega=\omega_{n}\), la respuesta retarda la excitación exactamente 90°, independientemente del nivel de amortiguación viscosa; esta llamada fase de cuadratura es una característica importante a menudo utilizada para ayudar a determinar las frecuencias naturales en las pruebas de vibración de máquinas y estructuras.
• Filtro de paso bajo de ^segundo orden Un sistema de ^segundo orden moderadamente amortiguado (\(0.5 \leq \zeta \leq 1\)) puede funcionar como un filtro de paso bajo,\(\omega_{n}\) siendo la frecuencia natural la frecuencia de ruptura (esquina). ^{Compare la curva de relación de magnitud para\(\zeta=1 / \sqrt{2}=0.707\) la Figura\(\PageIndex{1}\) con la curva de relación de magnitud para un filtro de paso bajo de primer orden, Figura 4.3.3. La diferencia más significativa entre las dos curvas se encuentra en sus asíntotas de alta frecuencia: la relación de magnitud de segundo orden se produce a razón de dos décadas por cada década de aumento de frecuencia (40 dB/década rolloff), dos veces más pronunciada que la relación de magnitud de primer orden.} Por lo tanto, el filtro de ^segundo orden funciona mucho más eficazmente que el filtro ^de primer orden. Sin embargo, una deficiencia práctica importante (en algunas aplicaciones potenciales) de ambos tipos de filtros de paso bajo es que imponen a la salida de paso bajo grandes retardos de fase en relación con la entrada.