11.1: Ecuaciones de Movimiento para un Cuerpo Rígido en Movimiento Plano General

Considera un cuerpo rígido que está restringido al movimiento en el\(xy\) plano. La figura\(\PageIndex{1}\) muestra el cuerpo en su posición de equilibrio estático de referencia (líneas continuas) y en una posición de movimiento (líneas discontinuas) relativa a la posición de referencia. El sistema de\(xy\) ejes mostrado es una referencia inercial con su origen en el punto\(O\), el cual es inmóvil o trasladándose a una velocidad constante. Utilizaremos vectores y operaciones vectoriales, por lo que necesitamos reconocer que el sistema de referencia inercial es realmente el sistema tridimensional de\(xyz\) ejes cartesianos, siendo el\(z\) eje perpendicular al\(xy\) plano y apuntando hacia nosotros, en el sentido de la regla de la derecha. Denotamos los vectores unitarios fijos en las direcciones cartesianas de referencia como\(\mathbf{1}_{\mathbf{x}}\),\(\mathbf{1}_{\mathbf{y}}\), y\(\mathbf{1}_{\mathbf{z}}\). Desde los antecedentes de tus cursos previos de dinámica y física, deberías estar familiarizado con vectores, álgebra y cálculo vectorial, y cinemática y dinámica vectorial; si es necesario, debes revisar estos conceptos en tu libro de texto de dinámica de ingeniería.

Figura\(\PageIndex{1}\): Cuerpo rígido en movimiento plano general

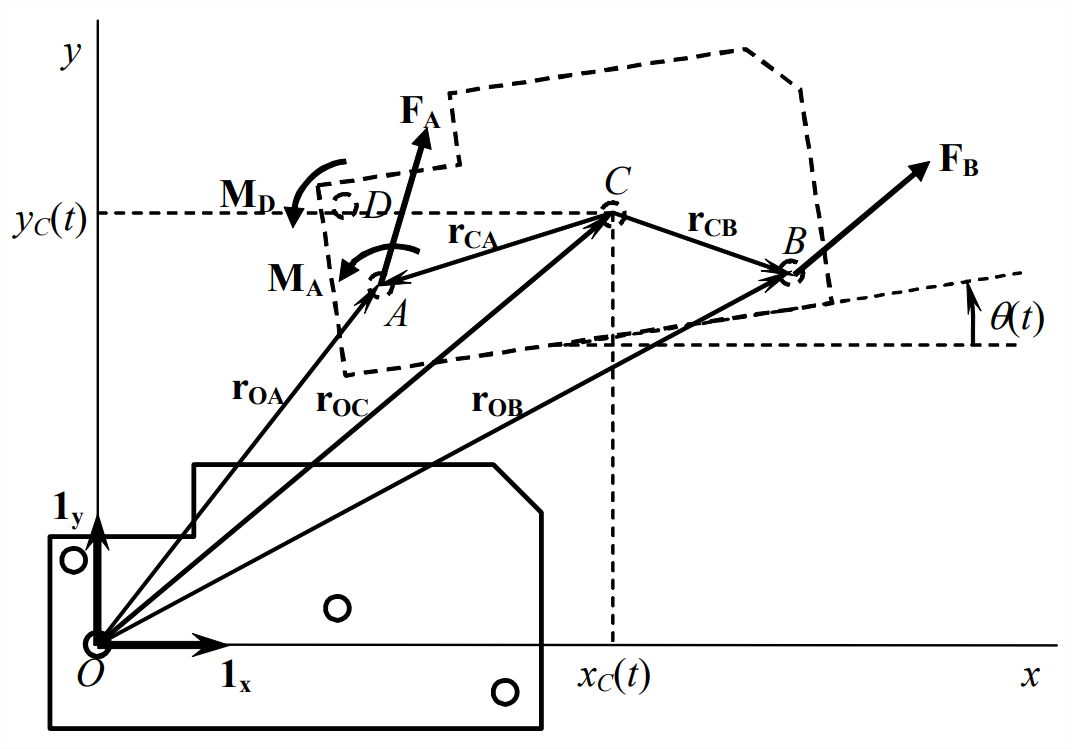
De particular interés es la posición y orientación del centro de masa del cuerpo rígido\(C\). En cualquier instante del tiempo\(t\),\(C\) tiene coordenadas de posición relativa\(\left[x_{C}(t), y_{C}(t)\right]\). Así, la posición del vector de\(C\) relativo a algún punto absolutamente fijo\(P\) es\(\mathbf{r}_{\mathbf{C}}(t)=\mathbf{r}_{\mathbf{o}}(t)+\mathbf{r}_{\mathbf{o C}}(t)=\mathbf{r}_{\mathbf{o}}(t)+x_{C}(t) \mathbf{1}_{\mathbf{x}}+y_{C}(t) \mathbf{1}_{\mathbf{y}}\), donde está la posición instantánea conocida de\(O\) relativo a\(P\). Del mismo modo, la velocidad vectorial de\(C\) relativa a punto absolutamente fijo\(P\) es\(\mathbf{v}_{\mathbf{C}}(t)=\mathbf{v}_{\mathbf{o}}(t)+\mathbf{v}_{\mathbf{O C}}(t)=\mathbf{v}_{\mathbf{o}}(t)+\dot{x}_{C}(t) \mathbf{1}_{\mathbf{x}}+\dot{y}_{C}(t) \mathbf{1}_{\mathbf{y}}\), donde\(\mathbf{v}_{\mathbf{o}}(t)\) está la velocidad constante de\(O\) relativo a\(P\). Porque\(\mathbf{v}_{\mathbf{o}}(t)\) es constante, la aceleración vectorial absoluta de\(C\) es\(\mathbf{a}_{\mathrm{C}}(t)=\mathbf{a}_{\mathrm{oc}}(t)=\ddot{x}_{C}(t) \mathbf{1}_{\mathrm{x}}+\ddot{y}_{C}(t) \mathbf{1}_{\mathrm{y}}\). Denotamos como\(\theta(t)\) la orientación rotacional positivo-antihoraria del centro de masa\(C\) (de hecho, de todo el cuerpo, ya que es rígido). Posición\(\mathbf{r}_{\mathbf{O}}(t)\) de\(O\) es conocida, así que si podemos determinar en cualquier instante las tres cantidades de movimiento\(x_{C}(t)\),\(y_{C}(t)\), y\(\theta(t)\), entonces podemos calcular a partir de geometría simple la posición de cualquier punto en el cuerpo rígido. Estas tres cantidades son independientes en el movimiento plano general, y solo estas tres [más conocidas\(\mathbf{r}_{\mathbf{O}}(t)\)] se requieren para describir completamente la posición en el espacio del cuerpo rígido. Por lo tanto\(x_{C}(t)\)\(y_{C}(t)\),, y\(\theta(t)\) se llaman grados de libertad, y el movimiento de cuerpo rígido plano general se llama un problema de tres grados de libertad (3-DOF).

Por generalidad, identificamos otros tres puntos fijados al cuerpo rígido, momento en el que las acciones (fuerzas o momentos) son aplicadas por fuentes externas al cuerpo. (En general, puede haber más o menos puntos de acciones aplicadas externamente; analizar tales situaciones requerirá sólo modificaciones menores a la presente derivación). El punto\(A\) es una conexión con el ambiente externo, posiblemente a través de resortes, amortiguadores, etc.; las acciones aplicadas en el Punto A son la fuerza de reacción vectorial\(\mathbf{F}_{\mathrm{A}}=F_{A x} \mathbf{1}_{\mathbf{x}}+F_{A y} \mathbf{1}_{\mathbf{y}}\) y el momento de reacción vectorial\(\mathbf{M}_{\mathrm{A}}=M_{A} \mathbf{1}_{\mathbf{z}}\). Es útil expresar la posición vectorial del punto A en términos de la del centro de masa\(C\):\(\mathbf{r}_{\mathbf{O A}}=\mathbf{r}_{\mathbf{O C}}+\mathbf{r}_{\mathbf{C A}}\) (ver Figura\(\PageIndex{1}\)). \(\mathbf{F}_{\mathbf{B}}=F_{B x} \mathbf{1}_{\mathbf{x}}+F_{B y} \mathbf{1}_{\mathbf{y}}\)Se aplica una fuerza vectorial arbitraria en el punto\(B\), y la posición del vector de ese punto se expresa como\(\mathbf{r}_{\mathrm{OB}}=\mathbf{r}_{\mathrm{OC}}+\mathbf{r}_{\mathrm{CB}}\). Por último, un momento vectorial arbitrario\(\mathbf{M}_{\mathbf{D}}=M_{D} \mathbf{1}_{\mathbf{z}}\) actúa en el punto\(D\).

Denotamos como\(m\) la masa del cuerpo rígido. La ^segunda ley de Newton para las fuerzas, escrita en forma vectorial, es

\[m \mathbf{a}_{\mathrm{C}}=\mathbf{F}_{\mathrm{A}}+\mathbf{F}_{\mathrm{B}}\label{eqn:11.1} \]

Expresar la ecuación\(\ref{eqn:11.1}\) en términos de componentes escalares da las dos ODEs escalares:

\[m \ddot{x}_{C}=F_{A x}+F_{B x}\label{eqn:11.2a} \]

\[m \ddot{y}_{C}=F_{A y}+F_{B y}\label{eqn:11.2b} \]

Denotamos como\(J_C\) la inercia rotacional del cuerpo rígido alrededor de un eje normal al plano de movimiento y que pasa por el centro de masa\(C\). La ^segunda ley de Newton para los momentos relevantes para este caso de movimiento plano-movimiento establece que el momento inercial alrededor del centro de masa\(C\) es igual a la suma de todos los momentos aplicados sobre el centro de masa\(C\); se expresa de la siguiente manera en notación vectorial, incluyendo productos de cruce vectorial:

\[J_{C} \ddot{\theta} \mathbf{1}_{\mathbf{z}}=\mathbf{r}_{\mathrm{CA}} \times \mathbf{F}_{\mathbf{A}}+\mathbf{r}_{\mathrm{CB}} \times \mathbf{F}_{\mathbf{B}}+\left(M_{A}+M_{D}\right) \mathbf{1}_{\mathbf{z}}\label{eqn:11.3} \]

A pesar de la notación vectorial, la ecuación\(\ref{eqn:11.3}\) es en realidad una ecuación escalar, porque los productos de cruce de vectores obviamente producen vectores en la\(z\) dirección; el uso de estos productos cruzados solo proporciona economía de notación ¹.

Veremos una aplicación de Ecuaciones de movimiento plano-general\(\ref{eqn:11.2a}\),\(\ref{eqn:11.2b}\), y\(\ref{eqn:11.3}\) a un sistema aeroelástico específico en la Sección 11.3 (Ejemplo 11-3); pero, primero, es apropiado desarrollar en la Sección 11.2 e ilustrar en la Sección 11.3 (Ejemplos 11-1 y 11-2) el caso especial de puro movimiento rotacional plano alrededor de un punto fijo.

¹ Para Ecuaciones\(\ref{eqn:11.2a}\),\(\ref{eqn:11.2b}\), y\(\ref{eqn:11.3}\), el sistema de\(xyz\) ejes de referencia es inercial, ya sea estacionario en el espacio o moviéndose a una velocidad de traslación constante, y el movimiento del cuerpo rígido se mide con relación a este sistema inercial. Sin embargo, para muchos problemas en la dinámica, es preferible derivar ecuaciones de movimiento utilizando un sistema de ejes de referencia que se fija en el cuerpo y se mueva con él. Un problema de movimiento de avión de este tipo es la rotación de avance de una pala de rotor de helicóptero con bisagras, según lo analizado por Bramwell, 1976, pp. 51-52.