12.3: Modos de vibración de un modelo típico sin amortiguar de un ala
- Page ID
- 84723
Del Ejemplo 11.3.3 de la Sección 11.3, el sistema se representa nuevamente en la Figura\(\PageIndex{1}\):
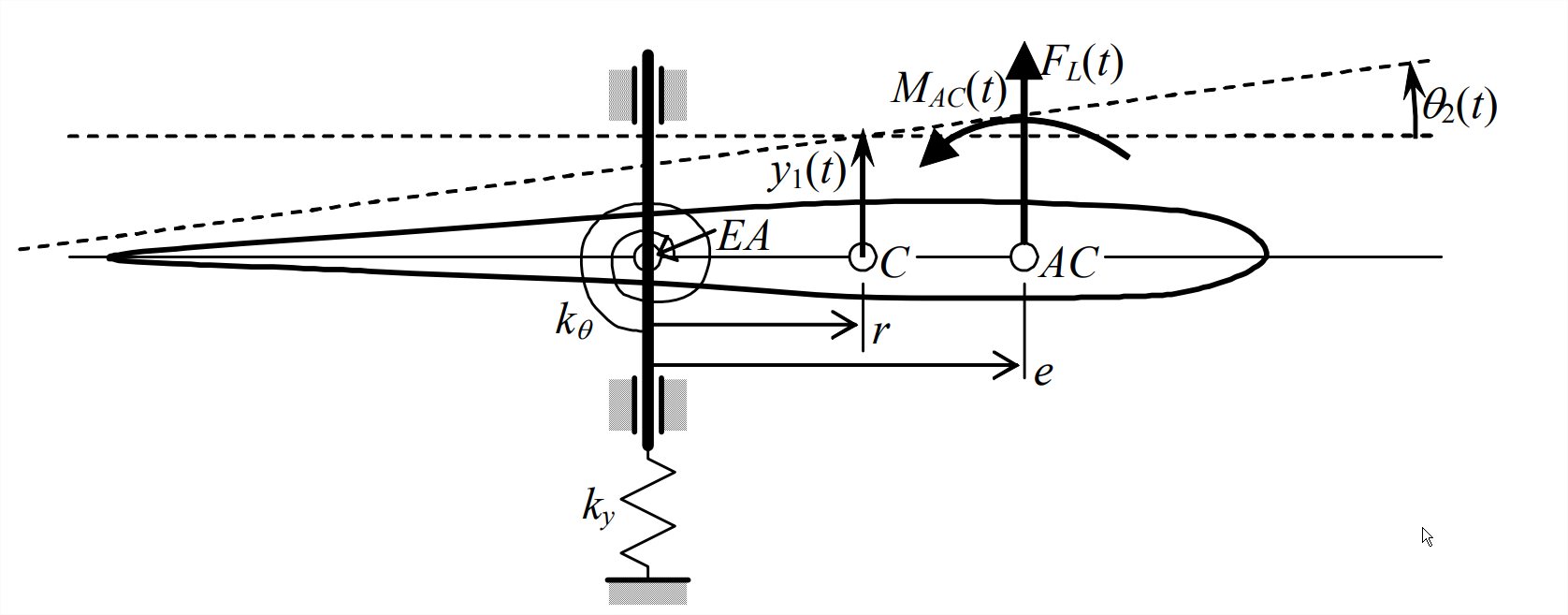
Los símbolos de grado de libertad\(y_{C}(t)\) y\(\theta(t)\) utilizados en el Capítulo 11 se cambian aquí, respectivamente, a\(y_{1}(t)\) y\(\theta_{2}(t)\), para denotar claramente que estas cantidades de movimiento son, respectivamente, grados de libertad (DOF) #1 y #2.
La ecuación matricial de movimiento en DOF\(y_{1}(t)\) y\(\theta_{2}(t)\), de la Ecuación 11.3.16 es
\ [\ left [\ begin {array} {cc}
m & 0\\
0 & J_ {C}
\ end {array}\ right]\ left [\ begin {array} {c}
\ ddot {y} _ {1}\
\ ddot {\ theta} _ {2}
\ end {array}\ right] +\ left [\ begin {array} {cc}
k_ {y} & -r k_ {y}\\
-r k_ {y} & k_ {\ theta} +r^ {2} k_ {y}
\ end {array}\ derecha]\ left [\ begin {array} {c}
y_ {1}\
\ theta_ {2}
\ end {array}\ right] =\ left [\ begin {array} {c}
F_ {L} (t)\\
(e-r) F_ {L} (t) +M_ {A C} (t)
\ final { array}\ derecho]\ label {eqn:12.25}\]
Para analizar la Ecuación\(\ref{eqn:12.25}\) para modos de vibración libre siguiendo el procedimiento descrito en el apartado anterior, establecemos a cero las acciones aerodinámicas aplicadas, y buscamos soluciones de movimiento del sistema no forzado en la forma:
\ [\ left [\ begin {array} {l}
y_ {1} (t)\
\ theta_ {2} (t)
\ end {array}\ right] =\ left [\ begin {array} {l}
Y_ {1}\
\ Theta_ {2}
\ end {array}\ right]\ cos\ omega t\ label {eqn:12.26}\
Sustituir la ecuación\(\ref{eqn:12.26}\) en ecuación\(\ref{eqn:12.25}\), cancelar el\(\cos \omega t\) término común y recopilar todos los coeficientes en una sola matriz cuadrada conduce a
\ [\ left [\ begin {array} {cc}
k_ {y} -\ omega^ {2} m & -r k_ {y}\\
-r k_ {y} & k_ {\ theta} +r^ {2} k_ {y} -\ omega^ {2} J_ {C}
\ end {array}\ derecha]\ izquierda [\ begin {array} c}
Y_ {1}\\
\ Theta_ {2}
\ end {array}\ derecha] =\ izquierda [\ comenzar {array} {l}
0\\
0
\ end {array}\ derecha]\ label {eqn:12.27}\]
Estableciendo a cero el determinante de la matriz de coeficientes da la ecuación cuadrática para las frecuencias naturales (la ecuación característica del problema de vibración libre),
Para valores físicamente realistas de los parámetros en Ecuación\(\ref{eqn:12.28}\), hay dos raíces reales positivas\(\omega_{1}^{2}<\omega_{2}^{2}\), una para cada uno de los modos de vibración,\(n=1,2\). Después de que se hayan encontrado estas raíces, pueden ser sustituidas de nuevo en cualquiera de las ecuaciones escalares de la ecuación matricial\(\ref{eqn:12.27}\) para dar ecuaciones para las formas de modo. Elegimos usar la primera ecuación escalar (porque tiene menos términos que la segunda), y resolvemos para el componente de forma de modo tono\(\Theta_{2}\) en términos de componente de traslación vertical\(Y_1\):
Existe una característica física interesante del movimiento en un modo de vibración pura que a veces es exhibida por cuerpos como el modelo de sección típica de la Figura\(\PageIndex{1}\), cuerpos que se trasladan y giran: mientras que la mayor parte del cuerpo está vibrando a una frecuencia natural\(\omega_{n}\), podría haber una particular punto en el cuerpo que está completamente inmóvil. Tal punto se llama nodo o punto nodal del modo de vibración. Podemos determinar la ubicación de un punto nodal en la sección típica haciendo referencia a la Figura\(\PageIndex{2}\), que muestra tanto el perfil aerodinámico en la posición de equilibrio estático como la línea de cuerda desplazada en algún instante arbitrario durante un ciclo de vibración modal pura. Definimos en el diagrama un\(x\) eje estacionario con su origen en el centro\(C\) de masa del perfil aerodinámico en la posición de equilibrio estático. El

La coordenada xnp se muestra en la intersección de la línea de cuerda de equilibrio estático y la línea de cuerda desplazada es el punto nodal. Usando la geometría de rotación pequeña y la notación en Figura\(\PageIndex{2}\), tenemos\(y_{1}(t) \approx-x_{n p} \theta_{2}(t)\); el signo menos es necesario porque\(x_{n p}\) como se muestra es negativo (popa del punto\(C\)), pero los valores de\(y_{1}(t)\) y\(\theta_{2}(t)\) mostrados son positivos. Por lo tanto, la ubicación del punto nodal para el modo de vibración\(n\) viene dada por
Si el modo\(n\) es mayormente traslación, con poca rotación, entonces la coordenada podría tener una magnitud tan grande que no haya un punto inmóvil a lo largo de la cuerda del perfil aerodinámico. Sin embargo, si hay un punto nodal en una sección típica en una prueba de vibración, se puede observar fácilmente rociando un poco de arena sobre el perfil aerodinámico cerca del punto nodal. A medida que el cuerpo vibra, la arena migrará lejos de las superficies oscilantes y se acumulará en el punto nodal inmóvil.
En lugar de tratar con un número excesivo de símbolos algebraicos en ecuaciones como la Ecuación\(\ref{eqn:12.28}\), ahora es conveniente considerar un ejemplo numérico. Una cierta sección típica de túnel de viento tiene una cuerda de 12 pulgadas, pesa\(mg\) = 5.00 lb, tiene un “peso” rotacional alrededor de su centro de masa\(J_{C} g\) = 90.0 lb-pulgada 2, y tiene su centro de masa ubicado\(r\) = 3.00 pulgadas adelante del eje en el que es soportado por un ligero flexible vigas que funcionan como resortes. Las constantes de resorte proporcionadas por las vigas son\(k_{y}\) = 51.0 lb/pulgada y\(k_\theta\) = 920 lb-pulgadas/radián. La sesión de MATLAB impresa a continuación evalúa ecuaciones\(\ref{eqn:12.28}\) a través\(\ref{eqn:12.30}\) de este caso numérico.
” mg=5.00; Jcg=90.0; r=3.00; g=386.1;% constantes de masa e inercia
” ky=51.0; kt=920; formato corto e% constantes de rigidez
” p= [mg*jcg/g^2 - (mg* (kt+ky*r^2) +JcG*ky) /g ky*kt] %coeffs de la Ec. (12-28)
p =
3.0187e-003 -2.9746e+001 4.6920e+004
” w_sqrd=raíces (p) %raíces w^2 de la ecuación cuadrática (12-28)
w_sqrd =
7.8822e+003
1.9720e+003
” wn= [sqrt (w_sqrd (2)) sqrt (w_sqrd (1))] %frecuencias naturales circulares (en rad/s) dispuestas en orden ascendente
wn =
4.4407e+001 8.8782e+001
” fn=wn/2/pi %frecuencias naturales cíclicas (en Hz)
fn =
7.0676e+000 1.4130e+001
” Th2n= (ky-mg/g*wn.^2)/(r*ky) %Eq. (12-29) para componentes de forma de modo\(\Theta\) 2n, con Y 1n = 1 pulgada
Th2n =
1.6642e-001 -3.3382e-001
” XnPN =( -1). /Th2n %Eq. (12-30) para ubicaciones de los puntos nodales
Los resultados numéricos de los cálculos de MATLAB se resumen en la siguiente tabla:
| Modo de vibración\(n\) | 1 | 2 |
| Frecuencia natural\(\omega_n\) y\(f_n=\omega_n/2 \pi\) |
\(\omega_1\)= 44.41 rad/s \(f_1\)= 7.068 Hz |
\(\omega_2\)= 44.41 88.78 rad/s \(f_2\)= 14.13 Hz |
| Forma de modo | \ (\ left [\ begin {array} {l} Y_ {11}\ \ Theta_ {21} \ end {array}\ right] =\ left [\ begin {array} {c} 1\ text {inch}\\ 0.1664\ mathrm {rad} \ end {array}\ right]\) |
\ (\ left [\ begin {array} {c} Y_ {12}\ \ Theta_ {22} \ end {array}\ right] =\ left [\ begin {array} {c} 1\ text {inch}\\ -0.3338\ mathrm {rad} \ end {array}\ right]\) |
| Ubicación del punto nodal\(\left(x_{n p}\right)_{n}\) | −6.01 pulgadas | +3.00 pulgadas |
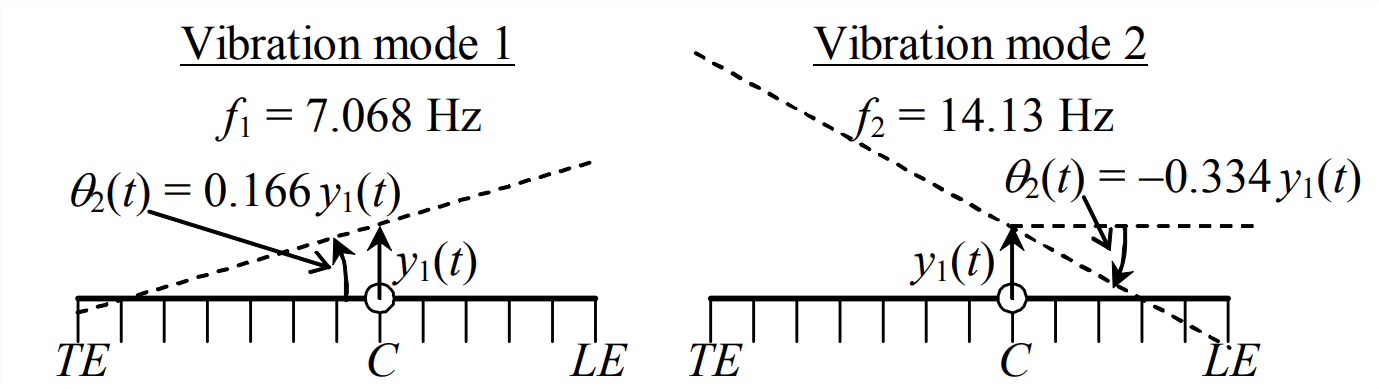
Los modos de vibración de esta sección típica también se muestran efectivamente en un formato gráfico, Figura\(\PageIndex{3}\), que es comparable a la Figura 12.2.2 para el sistema masa-resorte. La figura\(\PageIndex{3}\) indica el perfil aerodinámico en su posición de referencia con una línea de cuerda sólida, y en una posición desplazada modal con una línea de cuerda discontinua. Supongamos que el centro de masa\(C\) está ubicado a 5 pulgadas a popa del borde de ataque LE a lo largo de la cuerda de 12 pulgadas. En este caso, los puntos nodales de ambos modos (enumerados en la tabla anterior) se encuentran en el perfil aerodinámico como se muestra en la Fig. 12-6, no hacia delante\(LE\) ni hacia atrás del borde de salida\(TE\). Para mayor claridad gráfica, las magnitudes de los movimientos\(y_{1}(t)\) y se\(\theta_{2}(t)\) muestran muy exageradas en relación con el acorde de 12 pulgadas. Los movimientos reales de una sección típica realista serían decenas o cientos de veces más pequeños.