13.2: Diagrama de bloques de Laplace con ramas de retroalimentación
- Page ID
- 84675
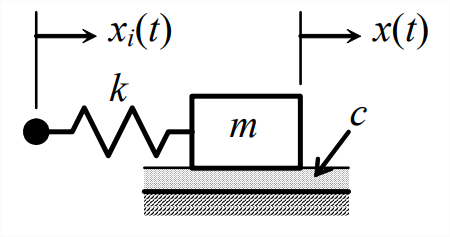
Pasemos más allá de los aspectos más básicos de los diagramas de bloques de Laplace analizando el\(k\) sistema\(m\) -\(c\) - con excitación de base que se muestra en la Figura\(\PageIndex{1}\). La entrada es la traslación\(x_i(t)\) base y la salida es la traslación masiva\(x(t)\). La ODE de movimiento para este sistema (de la tarea Problema 9.1) es
\[m \ddot{x}+c \dot{x}+k x=k x_{i}(t)\label{eqn:13.6} \]
Es conveniente denotar la transformada de entrada como\(L\left[x_{i}(t)\right]=X_{i}(s)\) y la transformada de salida como\(L[x(t)]=X(s)\). Tomando la transformada de Laplace de la ecuación\(\ref{eqn:13.6}\) con cero IC, con el propósito de derivar la función de transferencia, da
\[m s^{2} X(s)+c s X(s)+k X(s)=k X_{i}(s)\label{eqn:13.7} \]
Ecuación conduce\(\ref{eqn:13.7}\) claramente a la función de transferencia,
\[T F(s) \equiv \frac{X(s)}{X_{i}(s)}=\frac{k}{m s^{2}+c s+k}\label{eqn:13.8} \]
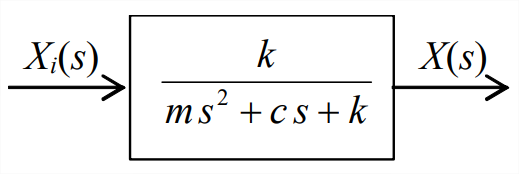
\(\ref{eqn:13.8}\)La ecuación se representa en el diagrama de bloques de Laplace de bucle abierto simple justo arriba.
Será instructivo para nuestro posterior estudio del control de retroalimentación desarrollar ahora un diagrama de bloques alternativo pero equivalente a partir de Ecuación\(\ref{eqn:13.7}\). Primero, transponemos al lado derecho todos los términos que no sean el\(X(s)\) término de orden superior:
\[m s^{2} X(s)=k X_{i}(s)-c s X(s)-k X(s)\label{eqn:13.9} \]
Ahora “resolvemos” algebraicamente para\(X(s)\) en el lado izquierdo de la Ecuación\(\ref{eqn:13.9}\) simplemente dividiendo por el coeficiente del lado izquierdo\(X(s)\):
Observe en Ecuación\(\ref{eqn:13.10}\) que la transformación de salida\(X(s)\) aparece tanto en los términos del lado derecho como en el lado izquierdo; estos términos del lado derecho implican retroalimentación. El uso de Ecuación\(\ref{eqn:13.10}\) conduce al siguiente diagrama de bloques con varios bloques de función de transferencia diferentes y con dos ramas de retroalimentación:
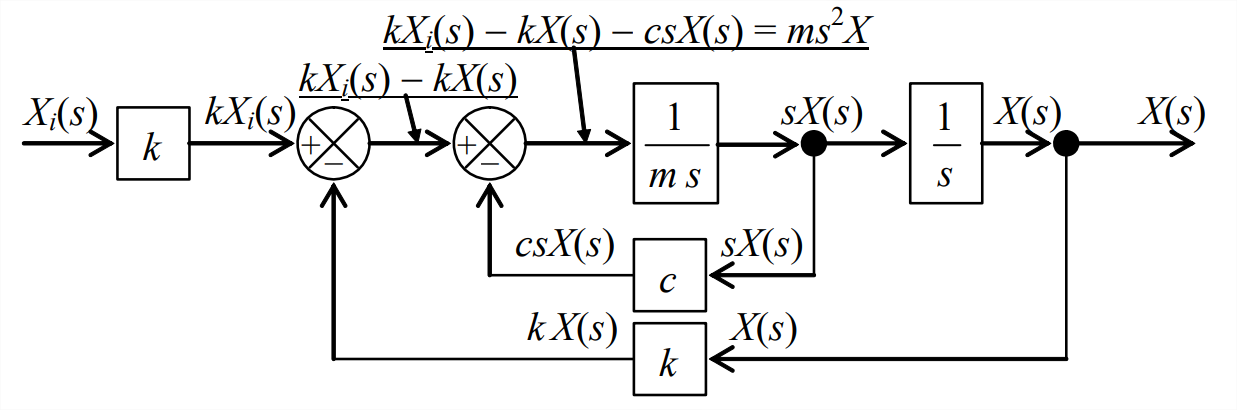
Las señales de entrada y salida para cada bloque están etiquetadas\(\PageIndex{3}\) en la Figura con el fin de ayudarle a relacionar el diagrama de bloques con la ecuación\(\ref{eqn:13.10}\), y debe comparar cuidadosamente la ecuación y el diagrama hasta que esté seguro de que entiende.
Además, diagrama de bloques Figura\(\PageIndex{3}\) introduce dos tipos de cruces. El primer tipo es un punto de ramificación simple (círculo negro), desde el cual la misma “señal” de salida de bloque viaja hacia adelante en dos ramas diferentes, como lo indican las etiquetas de señal en la Figura\(\PageIndex{3}\). El segundo tipo es una unión sumadora, que se muestra a la derecha con señales de entrada y salida etiquetadas. Esta unión sumadora está configurada para retroalimentación negativa, por lo que diferencia las dos señales de entrada,\(\operatorname{Out}(s)=\operatorname{In}_{1}(s)-\operatorname{In}_{2}(s)\).
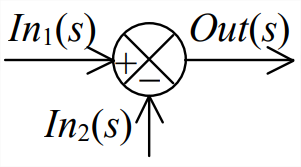
En esta sección, comenzamos con Ecuación ODE\(\ref{eqn:13.6}\) y desarrollamos a partir de ella el diagrama de bloques de Laplace Figura\(\PageIndex{3}\). Este enfoque es principalmente con el propósito de presentar algunas características importantes de los diagramas de bloques. Este enfoque es en realidad el reverso del procedimiento estándar para el análisis de los sistemas de control de retroalimentación, que consideraremos en capítulos posteriores. Ahí, comenzaremos con el diagrama de bloques de un sistema, algo así como Figura\(\PageIndex{3}\), y derivaremos de él la función de transferencia de bucle cerrado, CLTF (s)), que en este caso es solo Ecuación\(\ref{eqn:13.8}\). El proceso de\(CLTF(s)\) derivar del diagrama de bloques del sistema requerirá algunas operaciones nuevas en álgebra de diagrama de bloques; es conveniente posponer las descripciones de estas operaciones hasta que las necesitemos en capítulos posteriores.


