13.3: Respuesta Forzada de un Sistema m-c-k con Excitación Base

Será útil para nuestra introducción al control de retroalimentación en el Capítulo 14 si examinamos ahora la relación entre el movimiento de entrada\(x_{i}(t)\) y el movimiento de salida\(x(t)\) para el sistema mecánico de la Figura 13.2.1 y la Ecuación 13.2.1. Adoptemos aquí la perspectiva que queremos usar para controlar\(x(t)\);\(x_{i}(t)\) en particular para este sistema, supongamos que queremos hacer que el movimiento\(x(t)\) de masa\(m\) sea lo más cercano posible al movimiento de entrada\(x_{i}(t)\). Se puede visualizar intuitivamente desde la Figura 13.2.1 que si\(x_{i}(t)\) se impone muy lentamente, entonces\(x(t)\) será esencialmente lo mismo que\(x_{i}(t)\); en este caso, la fuerza inercial de la masa\(m\) será insignificante, y el resorte se\(k\) deformará solo ligeramente, por lo tanto actuando esencialmente como un eslabón rígido. (Por supuesto, se puede probar teóricamente este análisis cualitativo, por ejemplo, encontrando respuesta de frecuencia a una frecuencia de entrada muy baja.)

Pero, ¿\(x(t)\)se puede hacer el movimiento de salida cerca de la entrada\(x_{i}(t)\) si no\(x_{i}(t)\) se impone lentamente? Tu intuición probablemente no responde a esta pregunta porque, en este caso, la primavera\(k\) podría deformarse significativamente, y la fuerza inercial de la masa\(m\) podría no ser despreciable. Tendremos que analizar esta situación teóricamente. Hagámoslo especificando que el movimiento de entrada\(x_{i}(t)\) es una función escalonada de magnitud\(X_{H}\) impuesta en el tiempo\(t\) = 0. Una entrada de paso ideal no es simplemente rápida; de hecho, es la excitación base más rápida imaginable (aunque no físicamente realizable), porque la posición de la base cambia con velocidad infinita at\(t\) = 0 de\(x_{i}=0\) a\(x_{i}=X_{H}\). Entonces esta entrada ideal plantea un desafío formidable para el objetivo de control: ¿puede la traducción de salida\(x(t)\) aproximar de alguna manera razonable la traducción de entrada\(x_{i}(t)\), aunque inicialmente la traducción de entrada sea infinitamente rápida?

Para analizar este caso, primero adaptemos la Ecuación ODE 13.2.1 a la ODE estándar para sistemas amortiguados ^{de segundo} orden tal como se define en el Capítulo 9. Dividir la Ecuación 13.2.1 por\(m\), y luego aplicar las definiciones estándar La Ecuación 7.1.3 para la frecuencia natural no amortiguada\(\omega_{n}=\sqrt{k / m}\), y la Ecuación 9.1.6 para la relación de amortiguación viscosa,\(\zeta=c /(2 \sqrt{m k})\), arroja la ODE en la forma\(\ddot{x}+2 \zeta \omega_{n} \dot{x}+\omega_{n}^{2} x=\omega_{n}^{2} x_{i}(t)\). Al comparar esta ODE con la Ecuación 9.2.2 se muestra que la entrada\(x_{i}(t)\) para este\(k\) sistema particular excitado por bases\(m\) es exactamente igual a la cantidad de entrada estándar:\(x_{i}(t) \equiv u(t)\).\(c\) Definimos entrada de paso\(x_{i}(t)=X_{H} H(t)\). Por lo tanto\(X_{H} \equiv U\),, que es la magnitud general de entrada de paso de la Sección 9.6, y podemos escribir la solución de respuesta de paso para\(|\zeta|<1\) directamente desde la Ecuación 9.6.5:

\[x(t)=X_{H}\left[1-e^{-\zeta \omega_{n} t}\left(\cos \omega_{d} t+\frac{\zeta \omega_{n}}{\omega_{d}} \sin \omega_{d} t\right)\right], \text { for } 0 \leq t\label{eqn:13.11} \]

En Ecuación\(\ref{eqn:13.11}\), la frecuencia natural amortiguada es\(\omega_{d} \equiv \omega_{n} \sqrt{1-\zeta^{2}}\). Además, para su uso en la Figura\(\PageIndex{1}\), el periodo del sistema no amasado es\(T_{n}=2 \pi / \omega_{n}\). Recordemos que nuestro objetivo de control es hacer que el movimiento de salida sea al menos aproximadamente igual al movimiento de entrada. At\(t = 0\), el movimiento de entrada\(x_{i}(t)\) salta discontinuamente de 0 a\(X_{H}\), luego\(x_i\) permanece constante a partir de entonces, por lo que nos gustaría que el movimiento de salida se aproxime\(x(t)\) a esa entrada de paso lo más cerca posible. En particular, queremos que sea el valor final, de\(x(t)\) estado estacionario\(X_{H}\).

Es instructivo calcular y graficar Ecuación\(\ref{eqn:13.11}\) para unos pocos valores diferentes de\(\zeta\), asumiendo que el sistema está subamortiguado,\(0 \leq \zeta<1\). Los gráficos de respuesta escalonada se muestran en la Figura\(\PageIndex{1}\). Si el sistema no está amortiguado\(c = 0\), entonces la masa oscila para siempre (en teoría) sobre la posición final deseada,\(x=X_{H}\); en este caso ideal (con amortiguación cero), no se puede lograr el objetivo de control.

Figura\(\PageIndex{1}\): Control de excitación base de la posición de la masa para un\(k\) sistema\(m\)\(c\) - -. (Copyright; autor vía fuente)

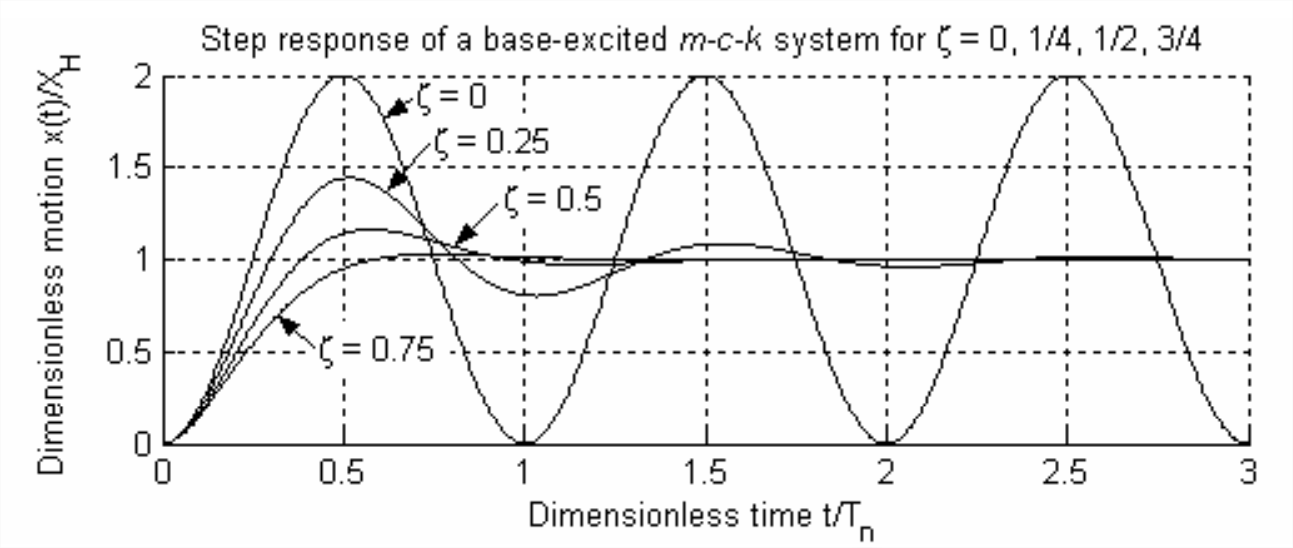
Sin embargo, la Figura\(\PageIndex{1}\) también demuestra que, si hay amortiguación positiva\(\zeta>0\), entonces la salida\(x(t)\) de movimiento, de hecho, se aproxima a la entrada de paso,\(x_{i}(t)=X_{H} H(t)\):\(x(t)\) se eleva desde 0, aunque con velocidad finita, y finalmente se asienta en el valor final deseado, \(x=X_{H}\).

Tenga en cuenta que las ecuaciones para especificaciones de respuesta escalonada (tiempo de subida, tiempo pico, relación máxima de sobreimpulso y tiempo de asentamiento) derivadas en la Sección 9.8 son aplicables a este caso de excitación de un\(k\) sistema\(m\)\(c\) - por movimiento base.

El sistema de masa-amortiguador-resorte excitado por base de la Figura 13.2.1 es un prototipo instructivo para el control de retroalimentación de salida de la posición mecánica, que es el tema del Capítulo 14. Por lo tanto, volveremos a referirnos a este sistema y a los resultados de las Secciones 13.2 y 13.3 para aclarar y justificar algunos de los desarrollos del sistema de control presentados en el Capítulo 14.