14.2: Definiciones y ejemplos de sistemas de control de bucle abierto

Como un intento inicial de producir el historial de movimiento deseado\(\theta(t)\), probablemente sea más natural simplemente buscar la configuración de entrada\(r(t)\) que haga el trabajo por completo, sin la necesidad de ningún refinamiento de diseño adicional. Este tipo de control se denomina control de bucle abierto, por razones que se darán más adelante. La figura\(\PageIndex{1}\) representa un sistema de control de bucle abierto.

Figura\(\PageIndex{1}\): Diagrama funcional del sistema de control de posición de rotor de bucle abierto. (Copyright; autor vía fuente)

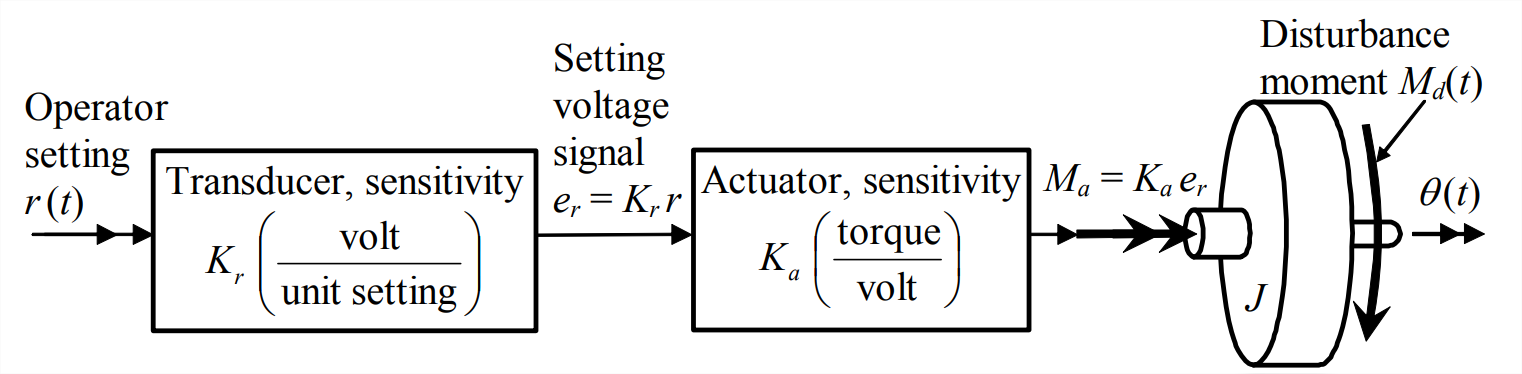
La configuración del operador\(r(t)\) se muestra en la figura\(\PageIndex{1}\) como una cantidad general, y se supone que el transductor de entrada es un dispositivo lineal general que produce una señal de voltaje\(e_{r}(t)=K_{r} r(t)\); si el dispositivo de entrada fuera un dial giratorio, por ejemplo, la configuración del operador podría ser una posición rotacional en grados, y el transductor podría ser una resistencia variable en un circuito divisor de voltaje (ver tarea Problemas 5.1 y 5.9), con sensibilidad calibrada con precisión de\(K_r\) voltios por grado. También se supone que el actuador es un dispositivo lineal general que produce momento de control\(M_{a}(t)=K_{a} e_{r}(t)=K_{a} K_{r} r(t)\); si se tratara de un actuador electromagnético, por ejemplo, probablemente consistiría en un amplificador de potencia y un motor, ambos diseñados para funcionar linealmente. En la práctica, las constantes de sensibilidad del dispositivo no tienen que ser positivas y muchas veces son negativas, pero supongamos aquí que todas son positivas (\(K_a > 0\),\(K_r > 0\), etc.) solo para evitar complicaciones innecesarias.

También se muestra en la Figura\(\PageIndex{1}\) el momento de perturbación\(M_{d}(t)\) que actúa sobre el rotor. En la terminología de control, una perturbación es alguna acción extraña sobre la planta, no la acción de control pretendida. En el sistema de la Figura\(\PageIndex{1}\), por ejemplo, un momento de actuador producido por ruido eléctrico no deseado en la circuitería sería una perturbación interna, y un momento producido por el viento o impacto de objetos sólidos sobre el rotor sería una perturbación externa. Las perturbaciones suelen ser aleatorias, o al menos impredecibles, por lo que normalmente no podemos escribir ecuaciones para describir su variación con el tiempo. En la mayoría de los casos, las perturbaciones tienden a influir negativamente en el desempeño de un sistema de control.

Analicemos el sistema de control de la Figura\(\PageIndex{1}\). El momento total que actúa sobre el rotor es\(M_{a}(t)+M_{d}(t)\), de manera que la Ecuación 14.1.1 se convierte

\[J \ddot{\theta}=M_{a}(t)+M_{d}(t)=K_{a} K_{r} r(t)+M_{d}(t)\label{eqn:14.4} \]

La perturbación\(M_{d}(t)\) en la ecuación\(\ref{eqn:14.4}\) es la némesis del control de bucle abierto, así que consideremos inicialmente el caso con perturbación cero,\(M_{d}(t)=0\). Si tenemos una ecuación para el historial de movimiento deseado\(\theta(t)\), entonces podemos resolver la ecuación\(\ref{eqn:14.4}\) directamente para la configuración del operador requerida:

\[r(t)=\frac{J}{K_{a} K_{r}} \ddot{\theta}\label{eqn:14.5} \]

Este método de búsqueda\(r(t)\) es fácil, y el control de bucle abierto parece ser una herramienta de ingeniería factible. Sin embargo, el control de bucle abierto tiene algunas deficiencias graves. Un ejemplo más detallado ayudará a revelar estas deficiencias, por lo que consideramos a continuación una aplicación de control de actitud de bucle abierto para una nave espacial.

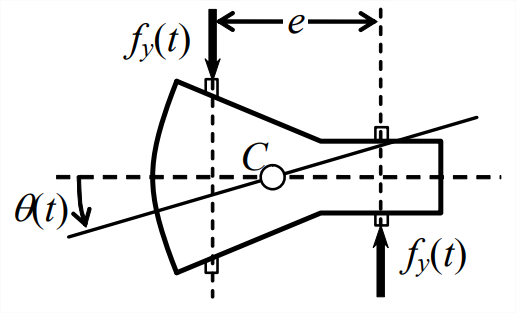
Supongamos que una cápsula que transporta astronautas está reingresando a la atmósfera terrestre\(\PageIndex{2}\), Figura, y que el ángulo de cabeceo\(\theta(t)\) debe ser controlado para posicionar el escudo térmico para un funcionamiento óptimo y evitar caídas inestables. Dos pares colineales de propulsores de gas (generalmente alimentados por productos químicos líquidos) están separados por el brazo de momento e de manera que accionan la rotación por un par (momento puro), sin provocar que el centro\(C\) de masa se traslada. El disparo de los dos propulsores mostrados activos en la Figura\(\PageIndex{2}\) produce un par positivo, y el disparo de los dos propulsores colineales opuestos produciría un par negativo. Para simplificar el análisis, supongamos que los propulsores son regulables continuamente, de modo que la fuerza de empuje se relaciona linealmente con la configuración del operador mediante

\[f_{v}(t)=K r(t)\label{eqn:14.6} \]

Figura\(\PageIndex{2}\): Control de paso de una cápsula de reentrada. (Copyright; autor vía fuente)

En Ecuación\(\ref{eqn:14.6}\),\(K\) es una constante de sensibilidad positiva, con dimensiones apropiadas dependiendo del carácter específico de\(r(t)\). Entonces el momento de control es\(M_{a}(t)=e f_{y}(t)=e K r(t)\), así que en la ecuación de movimiento equivalente a Ecuación\(\ref{eqn:14.4}\) es

\[J \ddot{\theta}=M_{a}(t)+M_{d}(t)=e K r(t)+M_{d}(t)\label{eqn:14.7} \]

en la que J es la inercia rotacional de la cápsula alrededor del centro de masa\(C\). Si descuidamos todas las perturbaciones posibles\(M_{d}(t)=0\), entonces podemos resolver la ecuación\(\ref{eqn:14.7}\) para la configuración del operador requerida en términos de la maniobra de cabeceo deseada:

\[r(t)=\frac{J}{e K} \ddot{\theta}\label{eqn:14.8} \]

Por ejemplo, exijamos que la nave espacial rote suavemente desde\(\theta = 0\) el ángulo de cabeceo final\(\theta=\theta_{f}\) durante\(t_f\) segundos, de acuerdo con la historia de tiempo inferior graficada en la Figura\(\PageIndex{3}\), que se expresa por la ecuación ¹

\[\theta(t)=\frac{\theta_{f}}{\pi}\left[\frac{\pi}{t_{f}} t-\frac{1}{2} \sin \left(\frac{2 \pi}{t_{f}} t\right)\right]\label{eqn:14.9} \]

para\(0 \leq t \leq t_{f}\). Diferenciar la Ecuación\(\ref{eqn:14.9}\) dos veces y luego sustituir el resultado en Ecuación\(\ref{eqn:14.8}\) lleva a

\[r(t)=r_{A} \sin \left(\frac{2 \pi}{t_{f}} t\right), \quad r_{A} \equiv \frac{2 \pi J \theta_{f}}{e K t_{f}^{2}}, \quad \text { for } 0 \leq t \leq t_{f}\label{eqn:14.10} \]

Esta configuración de entrada de referencia\(r(t)\) se muestra en la gráfica superior de la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Ejemplo de configuración del operador y maniobra de cabeceo resultante para la cápsula de reentrada. (Copyright; autor vía fuente)

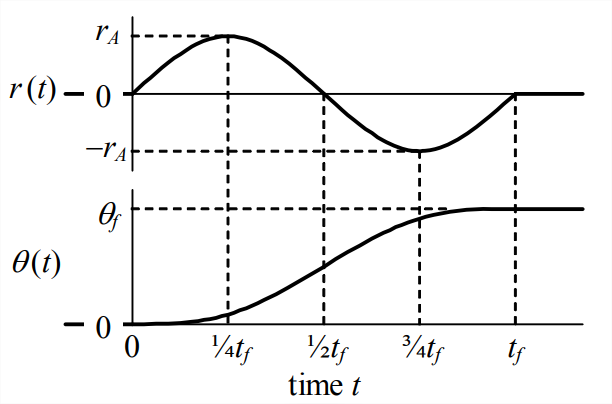
Nótese que Ecuaciones\(\ref{eqn:14.9}\)\(\ref{eqn:14.10}\) y Figura\(\PageIndex{3}\) ilustran el teorema impulso-momento para la rotación 1-DOF, que es directamente análogo al teorema impulso-momento para la traducción 1-DOF (Sección 8.2). El momento de control es proporcional a\(r(t)\)\(M_{a}(t)=e K r(t)\), por lo que el historial\(r(t)\) temporal muestra que el impulso de momento total (área bajo la curva de momento) en esta maniobra es cero; dado que el impulso total es cero, el momento angular final (\(t \geq t_{f}\)) también es cero,\(J \dot{\theta}=0\), por lo que la nave espacial es girado a la posición final\(\theta=\theta_{f}\) con velocidad rotacional final cero,\(\dot{\theta}=0\).

Hagamos una pausa para una revisión de la realidad. Una característica del equipo de control descrito para esta maniobra de nave espacial no es prácticamente realista: los propulsores de gas calificados para espacio de uso común son generadores de fuerza no lineales encendido-apagado (aproximadamente); no son regulables continuamente como se supone en este ejemplo, Ecuación\(\ref{eqn:14.6}\). De hecho, los propulsores de gas se utilizan para accionar el control de posición y actitud de las naves espaciales, pero su carácter de encendido-apagado produce un movimiento más áspero (cambios bruscos en la aceleración) que el de Equation\(\ref{eqn:14.9}\); ver Sarafin, 1995, pp. 636-637. Una maniobra suave como Ecuación\(\ref{eqn:14.9}\) sería accionada en la práctica por una rueda de reacción calificada para espacio o un giroscopio de momento de control. Hemos asumido los hipotéticos propulsores de gas estrangulado para este ejemplo solo porque es fácil visualizar esta situación y describirla en ecuaciones.

Ahora, con referencia al ejemplo anterior de control de actitud de naves espaciales, evaluemos el control de bucle abierto representado generalmente por la Figura\(\PageIndex{1}\), con particular interés en identificar las siguientes deficiencias:

1. Observe de la Figura\(\PageIndex{3}\) que la salida no\(\theta(t)\) es una función monótona de valor único de configuración del operador\(r(t)\). Por ejemplo, a\(r = 0\) allí corresponden tres valores de salida diferentes:\(\theta = 0\) antes de la maniobra,\(\theta=1 / 2 \theta_{f}\) durante la maniobra, y\(\theta=\theta_{f}\) después de la maniobra. Este tipo de relación funcional complicada no es necesariamente una deficiencia operativa, pero ciertamente es contraria a la expectativa de la ingeniería natural de una relación única, monótona y a menudo lineal entre causa y efecto.
2. Ecuaciones\(\ref{eqn:14.5}\)\(\ref{eqn:14.8}\), y\(\ref{eqn:14.10}\) muestran que la validez de la configuración\(r(t)\) derivada del operador depende directamente de la precisión de los parámetros de la planta y de las sensibilidades del sistema de control, y de la fidelidad del modelo teórico del sistema. Si, por ejemplo, utilizamos un valor inexacto de inercia rotacional\(J\) (una posibilidad distinta para la mayoría de los vehículos, ya que la quema de combustible cambia las inercias), o si los propulsores no funcionan exactamente como los modelamos, entonces el derivado\(r(t)\) claramente no conducirá al tiempo exacto de rotación deseado historia,\(\theta(t)\).
3. Las\(r(t)\) Ecuaciones\(\ref{eqn:14.5}\) y\(\ref{eqn:14.8}\) se predican en la ausencia de perturbaciones; pero si\(M_{d}(t) \neq 0\), entonces las derivadas no\(r(t)\) lograrán producir la exacta deseada\(\theta(t)\). En la práctica, los disturbios impredecibles son comunes, y no deben ignorarse. Por ejemplo, los momentos que pueden actuar sobre una nave espacial que vuelve a entrar podrían ser producidos por el arrastre atmosférico, el impacto de los desechos espaciales, los astronautas que cambian de posición dentro del vehículo, etc.

Las deficiencias 2 y 3 anteriores pueden describirse de una manera más general: el rendimiento de un sistema de control de bucle abierto depende en gran medida de la calidad del modelo teórico del sistema y su entorno; en otras palabras, el rendimiento del control es altamente sensible a las imperfecciones en el teórico modelo, que son inevitables para la mayoría de las situaciones reales de ingeniería. ²

Es una característica fundamental y debilidad del control de bucle abierto que la salida real no sea medida y comparada con la salida deseada, con el propósito de evaluar el error de salida e intentar reducir el error. Un remedio sencillo y natural para esta debilidad es “cerrar el bucle” con retroalimentación, que se describe en la siguiente sección. Tenga en cuenta que la ausencia de una rama de retroalimentación de la Figura\(\PageIndex{1}\) lleva a la designación “bucle abierto”. Pero incluso esta designación es al menos un poco engañosa porque no hay ningún “bucle”; ¡simplemente hay una sola rama que transporta señales que fluyen hacia adelante!

¹ Historia del tiempo de maniobra La ecuación\(\ref{eqn:14.9}\) proviene de Sarafin, 1995, páginas 644-645, un libro que incluye interesantes discusiones adicionales sobre el control de actitud de las naves espaciales.

² En el lenguaje de la ingeniería de control, un sistema de control se describe como robusto si su rendimiento y estabilidad son insensibles a influencias potencialmente perjudiciales como perturbaciones, deficiencias en el modelo teórico de la planta y mediciones de respuesta inexactas debido a dinámica del sensor.