14.5: Control de Circuito Cerrado de la Posición del Rotor (2)

Volvamos a visitar el sistema de control de posición-retroalimentación de la Sección 14.3 para, primero, evaluar su desempeño de control y, a continuación, desarrollar una adición al sistema que mejore el desempeño.

Es fácil evaluar el rendimiento del control con solo considerar la versión SISO de ODE of motion Equation 14.3.4, que es

\[J \ddot{\theta}+K_{a} K_{\theta} \theta=K_{a} K_{r} r(t)\label{eqn:14.19} \]

Como se señaló anteriormente, la respuesta pseudo-estática de Ecuación\(\ref{eqn:14.19}\) es\(\theta_{p s}(t)=\left[K_{r} / K_{\theta}\right] r(t)\); esta sería una buena respuesta controlada, pero no es necesariamente la respuesta total. Por lo tanto, consideremos con más detalle la respuesta transitoria total. \(\ref{eqn:14.19}\)La ecuación es una ODE de ^segundo orden no amortiguada del tipo analizado extensamente en el Capítulo 7. Al dividir la Ecuación\(\ref{eqn:14.19}\) por\(J\) y luego definir los parámetros apropiados, podemos adaptar esta ODE a la forma estándar Ecuación 7.1.5,\(\ddot{\theta}+\omega_{n}^{2} \theta=\omega_{n}^{2} u(t)\), en la que está la frecuencia natural\(\omega_{n}=\sqrt{K_{a} K_{\theta} / J}\), y la cantidad de entrada estándar es\(u(t)=\left[K_{r} / K_{\theta}\right] r(t)\). También podemos adaptar cualquier solución de respuesta adecuada ya derivada en los Capítulos 7 y 8 a este sistema de control de posición-retroalimentación. Por ejemplo, si la configuración del operador es la función de paso\(r(t)=R_{H} H(t)\), entonces\(u(t)=\left[K_{r} / K_{\theta}\right] R_{H} H(t) \equiv U H(t)\), entonces la solución estándar Ecuación 7.3.8 conduce a la respuesta de paso\(\theta(t)=\left(K_{r} / K_{\theta}\right) R_{H}\left(1-\cos \omega_{n} t\right)\). Esta respuesta escalonada se traza en la figura de la derecha, con el periodo definido como\(T_{n}=2 \pi / \omega_{n}\). Debido a la ausencia de amortiguación, la respuesta oscila para siempre sobre la respuesta seudoestática constante deseada,\(\theta_{p s}=\left(K_{r} / K_{\theta}\right) R_{H}\). La respuesta nunca se asienta\(\theta_{p s}\), por lo que el sistema de control no logra ofrecer el rendimiento deseado.

Figura\(\PageIndex{1}\) (Copyright; autor vía fuente)

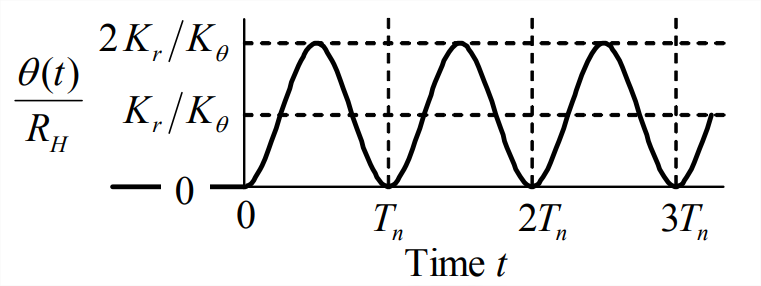
Debemos concluir de este ejemplo que la ausencia de amortiguación hace que el sistema de control de posición-retroalimentación de la Sección 14.3 (Figura 14.3.1) sea inadecuado para la mayoría, si no todas las aplicaciones de ingeniería de control. Sin embargo, hay una característica de diseño relativamente simple que se puede agregar al sistema de control, una característica que proporcionará amortiguación al sistema y mejorará en gran medida el rendimiento del control.

Figura\(\PageIndex{2}\): Diagrama de bloques de Laplace con ramas de retroalimentación para un\(k\) sistema\(m\) -\(c\) - excitado por bases. (Copyright; autor vía fuente)

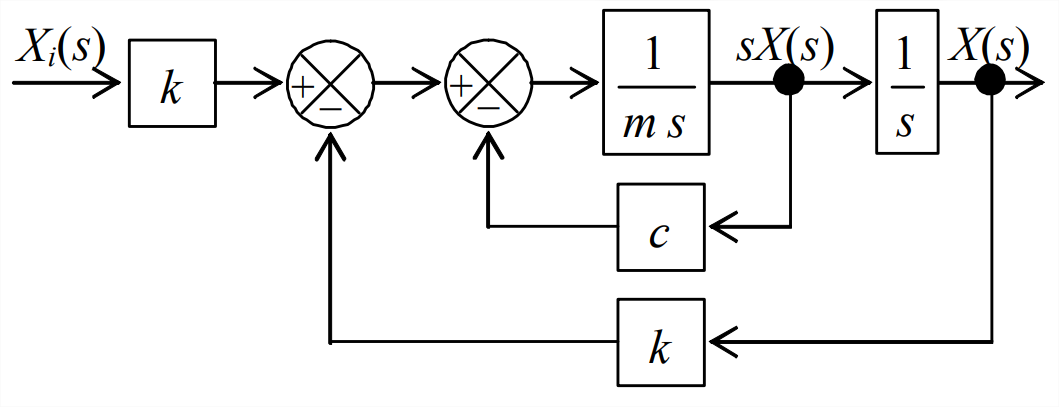
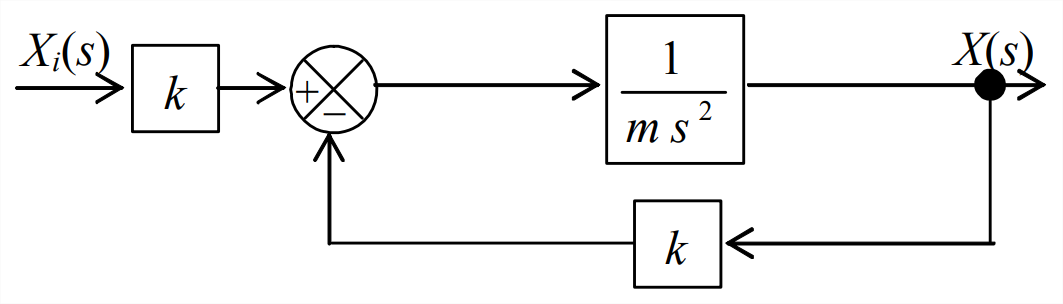
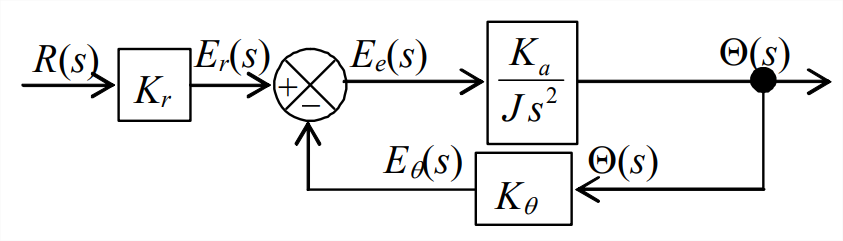
Con el fin de describir la motivación de esta nueva característica del diseño de control, volvamos a visitar el\(k\) sistema\(m\) -\(c\) - excitado por bases de las Secciones 13.2 y 13.3. Los elementos principales de la Figura 13.2.3, el diagrama de bloques de Laplace de ese sistema, se reproducen en la Figura\(\PageIndex{2}\). El bucle de retroalimentación interno hace que Figura sea\(\PageIndex{2}\) más complicado que cualquier diagrama de bloques del sistema de control que hayamos encontrado anteriormente en este capítulo. Considere, sin embargo, el caso de la amortiguación cero\(c = 0\), para lo cual el sistema es un sistema de masa-resorte (\(m\)-\(k\)) no amortiguado, excitado por la base, y la Figura\(\PageIndex{2}\) pierde el bucle de retroalimentación interno, adquiriendo la apariencia más simple de la Figura\(\PageIndex{3}\). Ahora, comparemos el diagrama de bloques de Laplace del sistema excitado por base (\(m\)-\(k\)) con el del sistema de control de posición-retroalimentación del rotor, Figura\(\PageIndex{4}\), que se repite aquí. Los diagramas de bloques de Laplace de los dos sistemas tienen formas casi idénticas,\(\PageIndex{4}\) siendo, por ejemplo, constantes\(K_r\) y\(K_{a} / J\) en Figura directamente análogas, respectivamente, a constantes\(k\) y\(1 / m\) en Figura\(\PageIndex{3}\). Solo la posibilidad en la Figura de\(\PageIndex{4}\) que la constante del bloque de entrada\(K_{r}\) y la constante del bloque de retroalimentación\(K_{\theta}\) puedan ser diferentes evita que la Figura\(\PageIndex{4}\) sea completamente análoga a la Figura\(\PageIndex{3}\). Se trata de una diferencia menor que no tiene efectos sustantivos en la siguiente discusión.

Figura\(\PageIndex{3}\): Diagrama de bloques de Laplace con rama de retroalimentación para un\(k\) sistema excitado por base\(m\). (Copyright; autor vía fuente)

Figura\(\PageIndex{4}\): Diagrama de bloques de Laplace del sistema de control de posición-retroalimentación SISO. (Copyright; autor vía fuente)

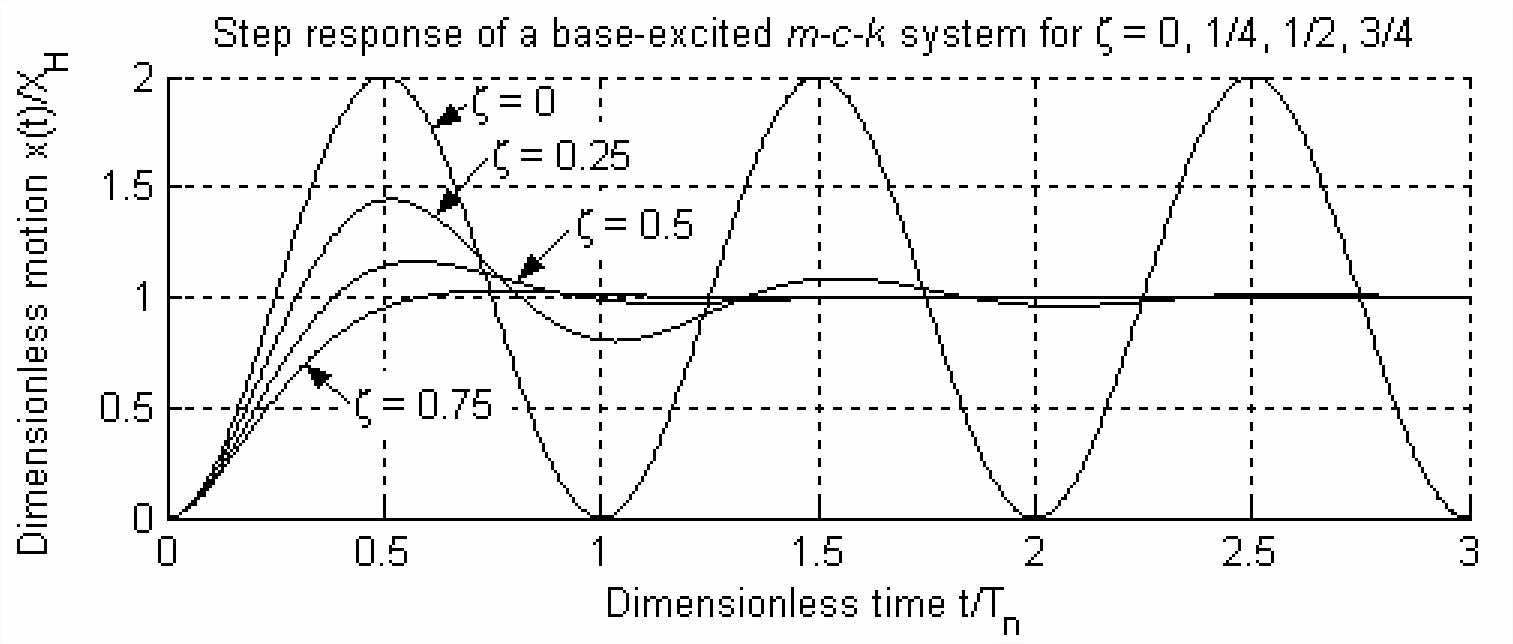
Explotemos las similitudes entre el\(k\) sistema\(m\) -\(c\) - excitado por bases y el sistema de control de la posición del rotor para guiarnos hacia un método para mejorar este último. Primero, nos referimos de nuevo a la solución en la Sección 13.3 para la respuesta del\(k\) sistema excitado por base\(m\) a la entrada escalonada\(x_{i}(t)=X_{H} H(t)\).\(c\) La respuesta de paso se presenta gráficamente en Figura\(\PageIndex{5}\), la cual se repite en la siguiente página para su conveniencia.

Recordemos las siguientes definiciones para el\(k\) sistema\(m\)\(c\) - -:\(\omega_{n}=\sqrt{k / m}\)\(T_{n}=2 \pi / \omega_{n}\), y\(\zeta=c /(2 \sqrt{m k})\). \(\PageIndex{5}\)Obsérvese en la Figura que la adición de amortiguación positiva (\(c>0 \Rightarrow \zeta>0\)) al sistema no amortiguado produce una salida\(x(t)\) que se aproxima a la entrada; por lo tanto, el\(k\) sistema\(m\) -\(c\) - amortiguado positivamente es, de hecho, un sistema de control adecuado, mientras que el sistema sin amortiguar\(m\) - \(k\)sistema no lo es.

Figura\(\PageIndex{5}\): Control de excitación base de la posición de la masa para un\(k\) sistema\(m\)\(c\) - -. (Copyright; autor vía fuente)

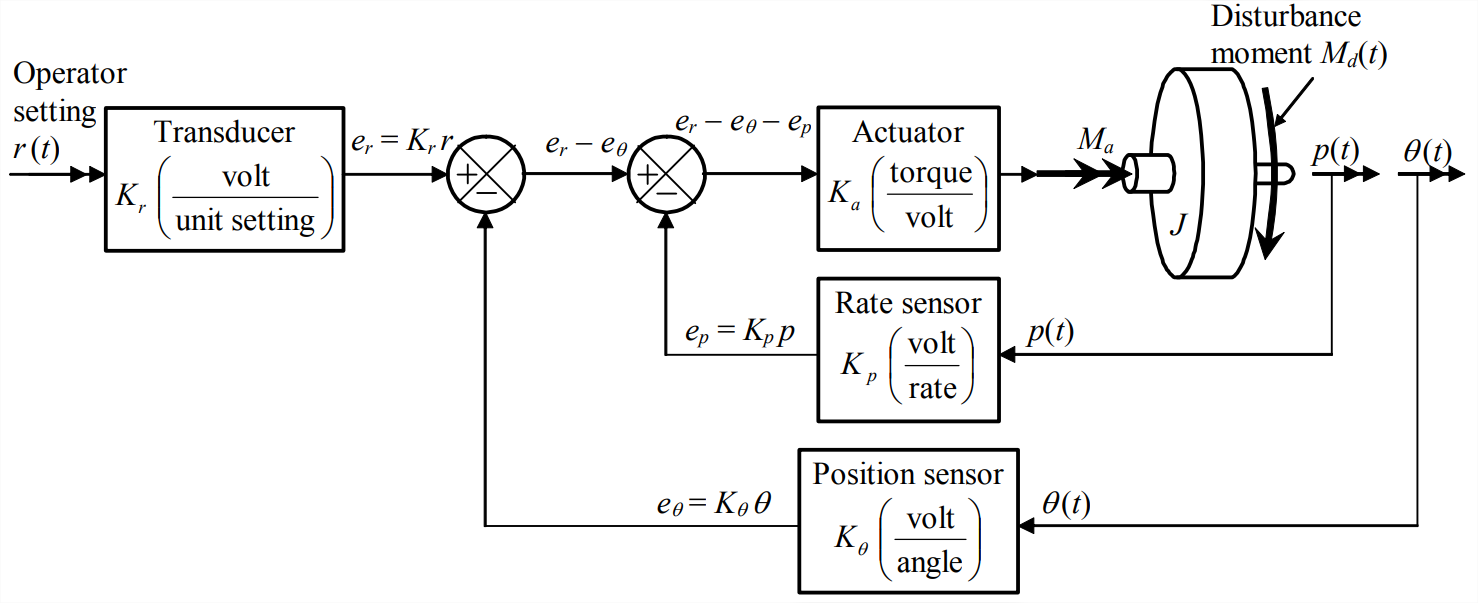
¿Podemos modificar el sistema de control de posición del rotor sin amortiguar de tal manera que tenga el mismo tipo de amortiguación positiva y, por lo tanto, un rendimiento de control adecuado, que el\(k\) sistema\(m\)\(c\) - -? Diagrama de bloques La figura\(\PageIndex{2}\) para el\(k\) sistema amortiguado\(m\) positivamente sugiere que podríamos mejorar el sistema de control de la posición del rotor agregando un bucle de retroalimentación interno a su diagrama de bloques\(\PageIndex{4}\), Figura, un bucle que es similar al bucle interno de la Figura\(\PageIndex{2}\).\(c\) Pero, ¿existen operaciones físicas prácticas y dispositivos correspondientes a la adición puramente matemática de este tipo de bucle al diagrama de bloques de Laplace Figura\(\PageIndex{4}\)? Para responder a esta pregunta, observemos que la señal de retroalimentación de Laplace del bucle interno en Figura\(\PageIndex{2}\) es\(s X(s)\), que es la transformada de Laplace de velocidad\(\dot{x}(t)\). Por lo tanto, el bucle interno de la Figura\(\PageIndex{2}\) representa matemáticamente las operaciones físicas de detectar la velocidad de salida y multiplicar esa velocidad por constante negativa\(−c\) para crear una fuerza de amortiguación que se opone al movimiento de la masa\(m\). Podemos realizar la operación física análoga para el sistema de control de posición del rotor midiendo la velocidad de rotación de salida\(p(t) \equiv \dot{\theta}(t)\) con un sensor apropiado (como un giroscopio de velocidad) y alimentando esa señal negativamente de nuevo a la entrada del actuador. La figura\(\PageIndex{6}\) representa el sistema de control de posición del rotor modificado, con esta retroalimentación de velocidad (para proporcionar amortiguación positiva) y la retroalimentación de posición original (para proporcionar rigidez positiva).

Figura\(\PageIndex{6}\): Diagrama funcional del sistema de control de posición de rotor con retroalimentación de posición y retroalimentación de velocidad. (Copyright; autor vía fuente)

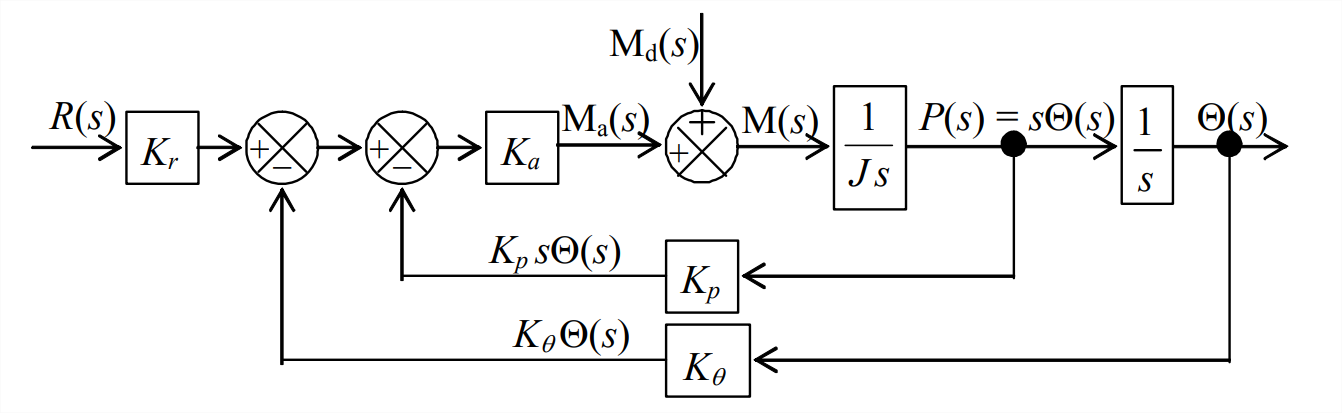
La Figura\(\PageIndex{7}\) es el diagrama de bloques de Laplace correspondiente al diagrama funcional Figura\(\PageIndex{6}\). Para medir y retroalimentar la velocidad de rotación, la forma apropiada de la planta ODE de movimiento Ecuación 14.1.1 es\(J \dot{p}=M(t)\), por lo que la función de transferencia de planta apropiada en el nuevo bucle interno es\(L[p(t)] / L[M(t)] \equiv P(s) / \mathrm{M}(s)=1 /(J s)\). Además, la definición de velocidad de rotación conduce a la función de transferencia de integración de rama delantera,\(\Theta(s) / P(s)=1 / s\). Comparando Figura\(\PageIndex{7}\) con Figura\(\PageIndex{2}\) para el\(k\) sistema\(m\) -\(c\) - excitado por base, vemos que los dos diagramas de bloques de Laplace tienen formas casi idénticas, excepto por la presencia del momento de perturbación en la Figura\(\PageIndex{7}\). Así, y para resumir, hemos modificado el sistema de control de posición del rotor para agregar amortiguación positiva, utilizando como modelo el\(k\) sistema\(m\) -\(c\) - excitado por base.

Figura\(\PageIndex{7}\): Diagrama de bloques de Laplace del sistema de control de posición de rotor con retroalimentación de posición y retroalimentación de velocidad. (Copyright; autor vía fuente)

Los tipos de control posición-retroalimentación y velocidad-retroalimentación ilustrados por las figuras\(\PageIndex{6}\) y\(\PageIndex{7}\) son operaciones de salida relativamente simples: este control implica no más que operaciones aritméticas básicas en las señales de salida detectadas, sin ninguna modificación de la señal de error en el rama delantera. El capítulo 15 introduce el control por operaciones de error de entrada, lo que implica operaciones matemáticas más generales sobre una sola señal de error.

A continuación, analicemos en detalle la versión SISO del sistema de control de posición de rotor modificado. Así, establecemos\(M_{d}(t)=0\) y\(\mathrm{M}_{\mathrm{d}}(s)=0\), y volvemos a dibujar Figura\(\PageIndex{7}\) como diagrama de bloques SISO Figura\(\PageIndex{8}\). Nuestros objetivos son: primero, derivar de\(\PageIndex{8}\) la Figura la función de transferencia de bucle cerrado,\(\operatorname{CLTF}(s) \equiv \Theta(s) / R(s)\); segundo, inferir de\(\operatorname{CLTF}(s)\) las características del sistema SISO.

Figura\(\PageIndex{8}\): Diagrama de bloques de Laplace del sistema de control de posición de rotor SISO con retroalimentación de posición y retroalimentación de velocidad. (Copyright; autor vía fuente)

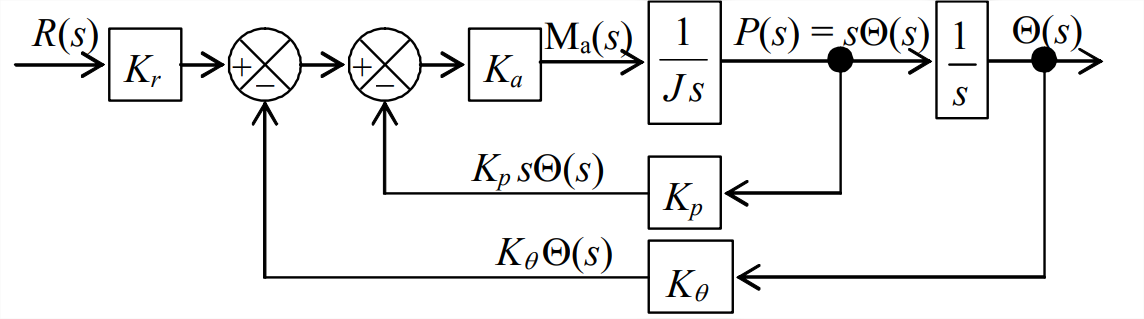
Podríamos resolver la Figura del diagrama de bloques\(\PageIndex{8}\) mediante el método de “fuerza bruta” de aplicar la Ecuación 14.4.7 primero al bucle interno, luego al bucle externo. Sin embargo, podemos lograr el mismo resultado de manera más simple usando algún álgebra sensible de diagrama de bloques. El enfoque en cada paso es modificar un bloque y/o rama para simplificar el diagrama sin cambiar las señales de salida más importantes. El primer paso obvio, es combinar los dos bloques en la rama delantera del bucle interno en la Figura\(\PageIndex{8}\) en función de transferencia\(K_{a} /(J s)\).

Figura\(\PageIndex{9}\) (Copyright; autor vía fuente)

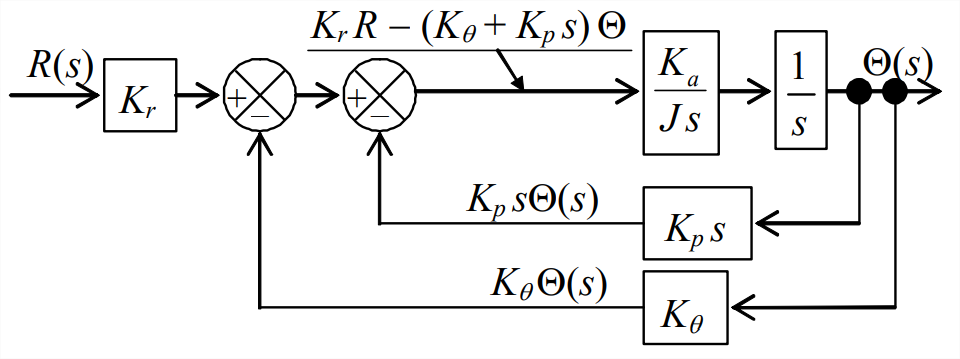
A continuación, movemos el punto de ramificación del bucle interno a la derecha del bloque de integración, y modificamos en consecuencia la función de transferencia de retroalimentación del bucle interno, como se muestra a continuación.

Figura\(\PageIndex{10}\) (Copyright; autor vía fuente)

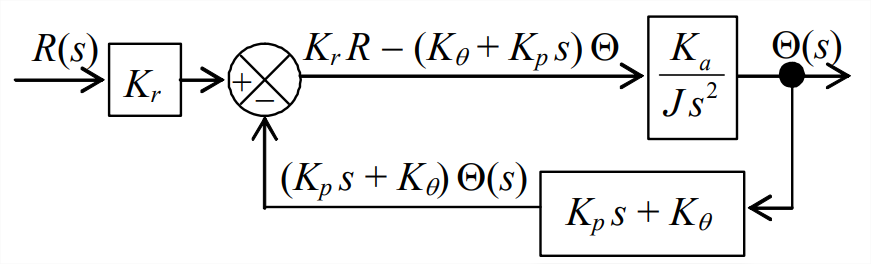
A continuación, multiplicamos los dos bloques de la rama hacia adelante dentro de los bucles en función de transferencia\(K_{a} /\left(J s^{2}\right)\). Ahora, ambas ramas de retroalimentación se originan esencialmente en el mismo punto de ramificación y terminan en la misma unión de suma, por lo que las combinamos en una sola rama de retroalimentación con una función de transferencia apropiada, como se muestra a la derecha. Este diagrama de bloques tiene un solo bucle, por lo que podemos aplicar la Ecuación 14.4.7 con los siguientes polinomios de función de transferencia:\(N_{G}=K_{a}\)\(D_{G}=J s^{2}\),\(N_{H}=K_{p} s+K_{\theta}\), y\(D_{H}=1\). El resultado es:

\[\frac{N_{G} D_{H}}{D_{G} D_{H}+N_{G} N_{H}}=\frac{K_{a} \times 1}{J s^{2} \times 1+K_{a} \times\left(K_{p} s+K_{\theta}\right)}=\frac{K_{a}}{J s^{2}+K_{a} K_{p} s+K_{a} K_{\theta}} \nonumber \]

Finalmente, multiplicar esta función de transferencia de bucle por la sensibilidad del transductor de entrada da

\[\operatorname{CLTF}(s) \equiv \frac{\Theta(s)}{R(s)}=\frac{K_{r} K_{a}}{J s^{2}+K_{a} K_{p} s+K_{a} K_{\theta}}\label{eqn:14.20} \]

Echemos la función de transferencia del sistema Ecuación\(\ref{eqn:14.20}\) en una forma que muestre más claramente las características fundamentales del sistema de bucle cerrado. Nuevamente utilizamos como guía el\(k\) sistema\(m\) -\(c\) - excitado por bases de la Sección 13.2. La frecuencia natural no amortiguada de ese sistema es\(\omega_{n}=\sqrt{k / m}\), y la relación de amortiguación viscosa es\(\zeta=c /(2 \sqrt{m k})\). Usando estas definiciones, podemos expresar la función de transferencia Ecuación 13.2.3 en términos de estas características fundamentales del sistema en lugar de los parámetros físicos\(m\)\(c\), y\(k\):

\[T F(s) \equiv \frac{X(s)}{X_{i}(s)}=\frac{k}{m s^{2}+c s+k}=\frac{k / m}{s^{2}+(c / m) s+k / m}=\frac{\omega_{n}^{2}}{s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}}\label{eqn:14.21} \]

Manipulando Ecuación\(\ref{eqn:14.20}\) de manera similar, con un paso adicional para dar cuenta de la posibilidad de que\(K_{r} \neq K_{\theta}\), da:

\[\operatorname{CLTF}(s) \equiv \frac{\Theta(s)}{R(s)}=\frac{K_{r}}{K_{\theta}} \times \frac{K_{a} K_{\theta} / J}{s^{2}+\left(K_{a} K_{p} / J\right) s+K_{a} K_{\theta} / J}=\frac{K_{r}}{K_{\theta}} \times \frac{\omega_{n}^{2}}{s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}}\label{eqn:14.22} \]

En Ecuación,\(\ref{eqn:14.22}\) la frecuencia natural no amortiguada y la relación de amortiguación viscosa del sistema de control de posición del rotor son

\[\omega_{n}=\sqrt{\frac{K_{a} K_{\theta}}{J}} \quad \text { and } \quad \zeta=\frac{K_{a} K_{p}}{2 J \omega_{n}}\label{eqn:14.23} \]

\(\ref{eqn:14.22}\)La ecuación difiere en forma de la ecuación\(\ref{eqn:14.21}\) solo en presencia de multiplicador pseudo-estático\(K_{r} / K_{\theta}\), que se define en la Ecuación 14.3.5.

El sistema con función de transferencia Ecuación\(\ref{eqn:14.21}\) se comporta como un sistema de control debe: en este caso, como un sistema amortiguado positivamente, ^{de segundo} orden. Por ejemplo, si los parámetros en Ecuación\(\ref{eqn:14.22}\) se seleccionan de tal manera que\(\zeta\) esté en el rango de 0.3 a 0.5, y si la configuración del operador es la función de paso\(r(t)=R_{H} H(t)\), entonces la transformada inversa de Laplace desarrollada en la tarea Problema 9.12 da el tipo de respuesta de paso que se muestra en la figura de la derecha. La salida no puede seguir exactamente esta entrada infinitamente rápida, pero se eleva rápidamente y se asienta rápidamente a la respuesta pseudo-estática deseada. Este ejemplo ilustra una característica general de los sistemas de control: generalmente es imposible lograr una precisión absoluta instantáneamente (en este caso, la respuesta pseudo-estática), pero un buen sistema de control puede lograr una precisión prácticamente aceptable, con un lapso de tiempo prácticamente aceptable entre la entrada y la salida deseada.

Se observó anteriormente que la retroalimentación de posición a través del sensor con ganancia\(K_{\theta}\) tiene el efecto de unir entre la configuración del operador y la inercia del rotor un resorte restaurador artificial con rigidez constante\(K_{a} K_{\theta}\). Vemos ahora, adicionalmente, que la retroalimentación de velocidad a través del sensor con ganancia\(K_{p}\) tiene el efecto de imponer sobre el movimiento absoluto del rotor un amortiguador viscoso artificial con constante de amortiguación\(K_{a} K_{p}\).

Finalmente, observemos que el desempeño favorable y estable de este sistema de control de posición de rotor depende fuertemente de la positividad de las constantes\(K_{a} K_{\theta}\) y\(K_{a} K_{p}\). En la práctica, es posible (de hecho, demasiado fácil) hacer negativas estas constantes, generalmente por accidente o negligencia, lo que podría provocar que el sistema sea inestable. Los capítulos 16 y 17 examinan con más detalle el importante tema de la estabilidad del sistema.