14.7: Capítulo 14 Tarea

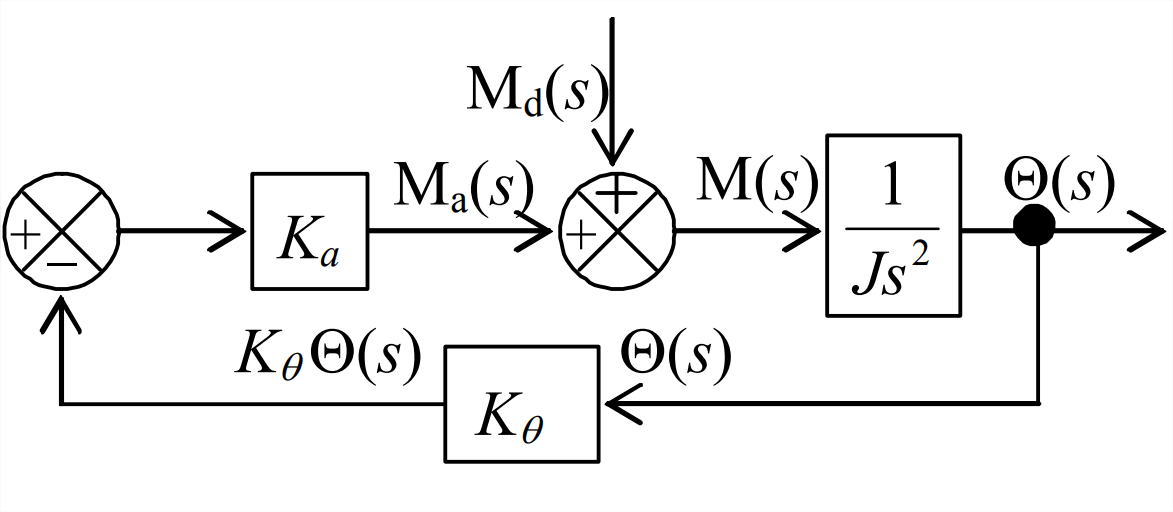
1. En la Sección 14.3 para el sistema de control de posición del rotor con retroalimentación de posición, la función de transferencia que relaciona la posición del rotor de salida con la configuración del operador de entrada, con perturbación cero, se deriva mediante una serie de operaciones algebraicas de diagrama de bloques para resolver (simplificar) Figura 14.3.3. En la práctica, para la evaluación de la calidad del sistema de control, a menudo se requiere también determinar la función de transferencia que relaciona la posición del rotor de salida con la perturbación, con ajuste cero del operador. El diagrama de bloques apropiado para esa tarea en este caso proviene de la Figura 14.3.2, con\(R(s) = 0\), como se muestra a la izquierda. Derivar de este diagrama de bloques la función de transferencia\(\frac{\Theta(s)}{\mathrm{M}_{\mathrm{d}}(s)}=\frac{1}{J s^{2}+K_{e} K_{\theta}}\). Esta tarea no es difícil: solo escribe\(\mathrm{M}_{\mathrm{a}}(s)\) en términos de\(\Theta(s)\), entonces\(\mathrm{M}(s)=\mathrm{M}_{\mathrm{a}}(s)+\mathrm{M}_{\mathrm{d}}(s)\), y\(\mathrm{M}(s) \times 1 / J s^{2}=\Theta(s)\), qué pasos deberían llevarte al resultado requerido. Este resultado también se puede derivar directamente de la ODE de movimiento Ecuación 14.3.4, pero la asignación aquí es derivarlo del diagrama de bloques, para darle práctica con álgebra de diagrama de bloques.

   

   Figura\(\PageIndex{1}\) (Copyright; autor vía fuente)

2. En algunos sistemas, la información se alimenta tanto hacia adelante como hacia atrás. Cada uno de los diagramas de bloques de Laplace La figura\(\PageIndex{2}\) y que\(\PageIndex{3}\) se muestra a continuación incluye tanto una rama de alimentación directa como una rama de retroalimentación de unidad. Transferir funciones\(F(s)\) y\(G(s)\) representar elementos arbitrarios de planta, filtro, sensor, etc. del sistema. (También podríamos incluir un bloque de función de transferencia en la rama unidad-retroalimentación, pero su valor sería simplemente 1, por lo que es una práctica estándar omitir ese bloque obvio). Para la (s) parte (s) asignada (s), derivar la ecuación algebraica para la función de transferencia del sistema\(X(s) / R(s)\),, en términos de\(F(s)\) y\(G(s)\).

   1. 

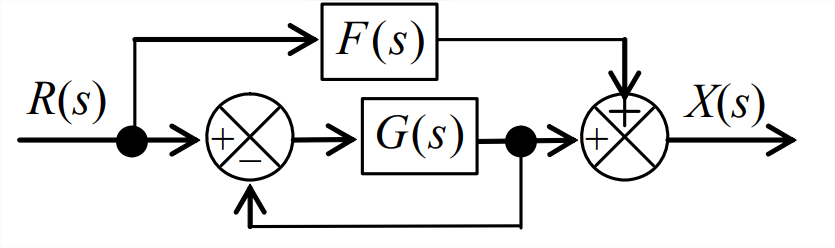
      Figura\(\PageIndex{2}\) (Copyright; autor vía fuente)

   2. 

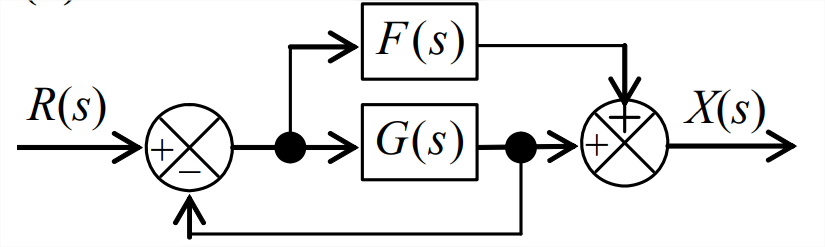
      Figura\(\PageIndex{3}\) (Copyright; autor vía fuente)

   3. El filtro mecánico de paso alto amortiguador-resorte de serie idealizado que se muestra en la Figura 3.7.4 tiene la ODE gobernante con dinámica del lado derecho (RHS)\(\dot{x}_{o}+\left(1 / \tau_{1}\right) x_{o}=\dot{x}_{i}(t)\), Ecuación 3.7.6. La función de transferencia de esta ODE es claramente\(X_{o}(s) / X_{i}(s)=s /\left(s+1 / \tau_{1}\right)\), dónde\(L\left[x_{i}(t)\right] \equiv X_{i}(s)\) y\(L\left[x_{o}(t)\right] \equiv X_{o}(s)\). Con la definición de una nueva variable independiente\(x_{d}(t)\) y la ecuación auxiliar\(x_{o}(t)=x_{d}(t)+x_{i}(t)\), la ODE se convierte en una forma alternativa sin dinámica RHS\(\dot{x}_{d}+\left(1 / \tau_{1}\right) x_{d}=-\left(1 / \tau_{1}\right) x_{i}(t)\), Ecuación 3.7.8. Construya un diagrama de bloques de Laplace usando la ODE alternativa y la ecuación auxiliar; este diagrama debe tener entrada\(X_{i}(s)\) a la izquierda y salida\(X_{o}(s)\) a la derecha, y debe incluir una rama de alimentación directa. Utilice álgebra de diagrama de bloques en este diagrama para derivar nuevamente la función de transferencia del sistema\(X_{o}(s) / X_{i}(s)=s /\left(s+1 / \tau_{1}\right)\).
3. Considera un sistema representado por el diagrama de bloques de Laplace algo general a la derecha. Constante\(K_{r}\) es una ganancia del sensor de entrada, y funciones de transferencia\(G_{1}(s)\)\(G_{2}(s)\),\(H_{1}(s)\), y\(H_{2}(s)\) representan elementos arbitrarios de la planta, filtro, sensor, etc. del sistema. Utilice álgebra de diagrama de bloques para mostrar en detalle que la función de transferencia de bucle cerrado es\[\operatorname{CLTF}(s) \equiv \frac{X(s)}{R(s)}=\frac{K_{r} G_{1} G_{2}}{1+G_{1} H_{1}+G_{1} G_{2} H_{2}} \nonumber \]

   

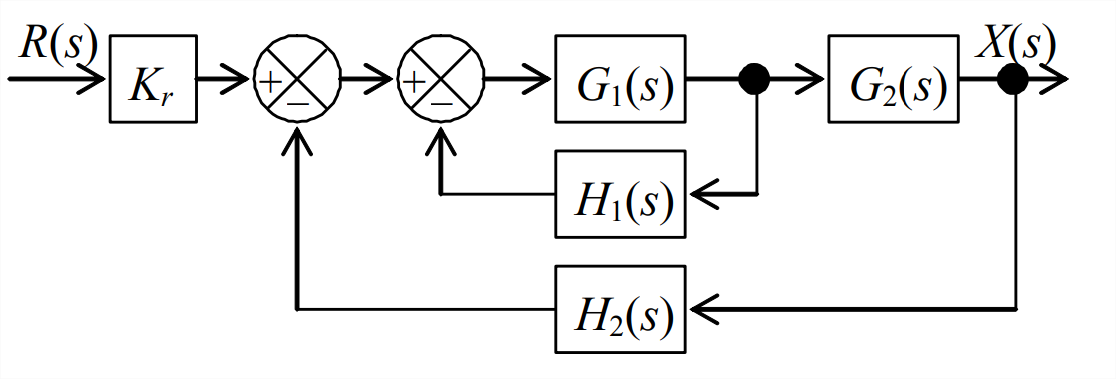
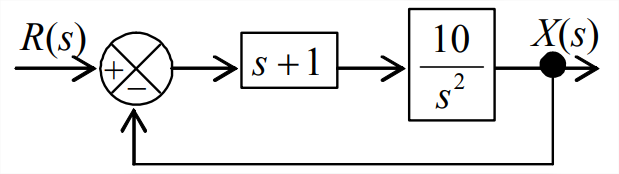
   Figura\(\PageIndex{4}\) (Copyright; autor vía fuente)

4. Considera un sistema representado por el diagrama de bloques a continuación. La rama de retroalimentación es una ruta unidad-retroalimentación; podríamos incluir un bloque de función de transferencia en esa rama, pero su valor sería simplemente 1, por lo que es una práctica estándar omitir ese bloque obvio.
   1. Mostrar que la función de transferencia de bucle cerrado es\[C L T F(s)=\frac{X(s)}{R(s)}=\frac{10(s+1)}{s^{2}+10 s+10} \nonumber \]

      

      Figura\(\PageIndex{5}\) (Copyright; autor vía fuente)

   2. Evaluar la ecuación cuadrática del denominador para calcular la relación de amortiguación viscosa\(\zeta\), lo que debería indicar que el sistema de bucle cerrado está sobreamortiguado.
   3. Facturar el denominador cuadrático en la forma\(\left(s-p_{1}\right)\left(s-p_{2}\right)\), encontrar los valores de los polos\(p_{1}\) y\(p_{2}\). (respuesta parcial:\(p_{1}=-1.127\) s ⁻¹)
   4. Supongamos que los CI son cero y que la entrada es una función de paso,\(r(t)=5 H(t)\). Determinar la ecuación algebraica completa para la salida\(x(t)\). Primero expresa\(X(s)\) en una expansión de fracción parcial, luego encuentra la transformada inversa de Laplace. Usa tu\(x(t)\) ecuación para encontrar el valor final, después de todo\(\lim _{t \rightarrow \infty} x(t)\), el movimiento dinámico se ha amortiguado. (respuesta parcial: uno de los términos en la ecuación para\(x(t)\) debe ser\(-5.728 e^{-8.873 t}\).)
5. Considere el control de posición de una rueda de reacción (de la Sección 3.3) por retroalimentación de posición más retroalimentación de velocidad, para lo cual el diagrama de bloques de Laplace del sistema es:

   

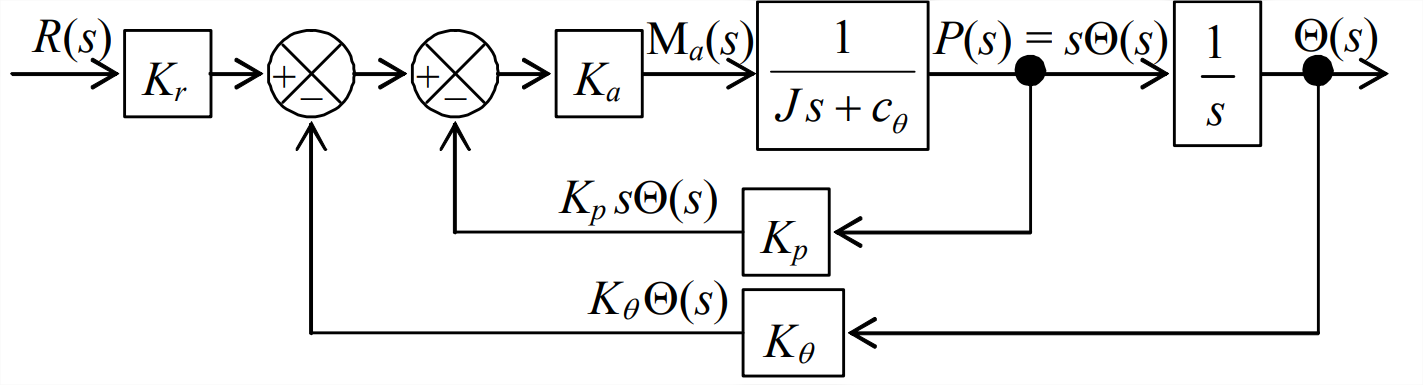
   Figura\(\PageIndex{6}\) (Copyright; autor vía fuente)

   Este diagrama de bloques es idéntico a la Figura 14.5.8, excepto que la función de transferencia de planta de la Ecuación 3.3.2 se debe\(1 /\left(J s+c_{\theta}\right)\)\(1 / J s\), no solo, a la presencia de fricción del rodamiento con supuesta constante de amortiguación viscosa\(c_{\theta}\). Se midieron los siguientes datos para un pequeño conjunto de rueda de reacción de laboratorio:\[J=2.56 \times 10^{-3} \mathrm{lb} \text { -inch-sec }^{2}, c_{\theta}=0.020 \frac{\text { ounce inch }}{\mathrm{rad} / \mathrm{s}}, K_{a}=0.950 \frac{\text { ounce inch }}{\mathrm{V}} \nonumber \] Para los casos asignados, las sensibilidades del transductor y del sensor del sistema de control son las que se muestran en las columnas 2, 3 y 4 de la siguiente tabla:

   Caso	\(K_{r}\)(V/rad)	\(K_{\theta}\)(V/rad)	\(K_{p}\)(VS/Rad)	\(t_{r}\)(s)	\(\bar{x}_{p}\)
   1	15	10	0.36	0.1280	0.3858
   2	1.5	1.5	0.27	0.4507	0.1117
   3	14	21	0.35	0.08163	0.5355
   4	3.5	3.5	0.24	0.2255	0.3260

   1. Calcule a partir de los valores de las columnas de la tabla 2, 3 y 4 las siguientes cantidades para este sistema de bucle cerrado: multiplicador pseudo-estático\(K_{r} / K_{\theta}\), frecuencia natural no amortiguada\(\omega_{n}\) (rad/s)\(\zeta\), relación de amortiguación viscosa y frecuencia natural amortiguada\(\omega_{d}\) (rad/s).
   2. Supongamos que la entrada es una función de paso,\(r(t)=R_{H} H(t)\), con\(R_{H}=30\) grados de magnitud. Para la respuesta escalonada posterior, calcule el tiempo de subida\(t_{r}\), el tiempo pico\(t_{p}\), la relación\(\bar{x}_{p}\) máxima de sobreimpulso y el tiempo de asentamiento\(t_{s}\) (ver Sección 9.8). Además, calcule el valor estático final de la posición de la rueda,\(\lim _{t \rightarrow \infty} \theta(t)\) en grados, después de que todo el movimiento dinámico se haya amortiguado. Las respuestas parciales se dan en las columnas 5 y 6 de la tabla anterior para ayudarte a saber si estás, o no estás en el camino correcto, pero aún debes mostrar todas las derivaciones y cálculos que conduzcan a estas respuestas.
   3. Para la misma entrada de paso que en la parte 14.5.2, use MATLAB para calcular y trazar la respuesta de paso\(\theta(t)\) en grados desde\(t=0\) hasta al menos el tiempo de asentamiento\(t=t_{s}\).
6. En la Sección 14.5 para el sistema de control de posición del rotor con retroalimentación de posición y retroalimentación de velocidad, la función de transferencia que relaciona la posición\(\Theta(s)\) del rotor de salida con la configuración del operador de entrada\(R(s)\), con perturbación cero, se deriva mediante una serie de operaciones algebraicas de diagrama de bloques para resolver (simplificar) Figura 14.5.8. En la práctica, para la evaluación de la calidad del sistema de control, a menudo se requiere también determinar la función de transferencia que relaciona la posición del rotor de salida con la perturbación, con ajuste cero del operador. El diagrama de bloques de Laplace apropiado para esa tarea en este caso proviene de la Figura 14.5.7, con\(R(s) = 0\), como se muestra en la figura a la derecha. Derivar de este diagrama de bloques la ecuación algebraica para la función de transferencia\(\frac{\Theta(s)}{\mathrm{M}_{\mathrm{d}}(s)}\).

   

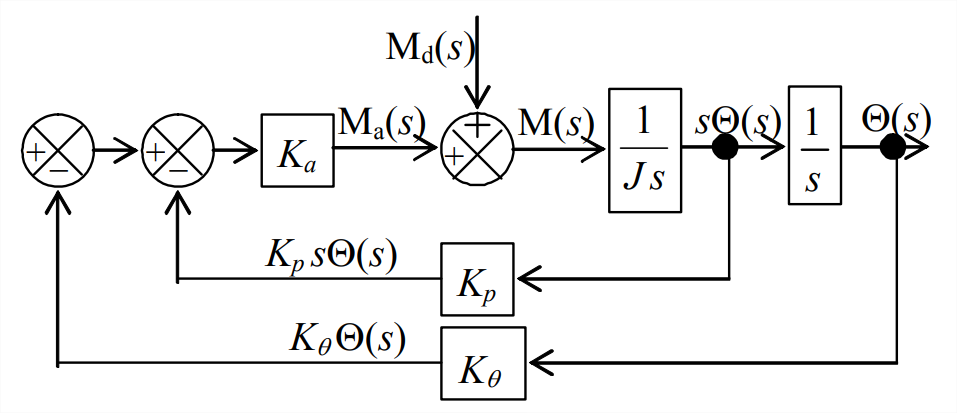
   Figura\(\PageIndex{7}\) (Copyright; autor vía fuente)

7. Considere un sistema representado por el diagrama de bloques de Laplace a la derecha. La rama externa de retroalimentación es una ruta de retroalimentación unitaria; podríamos incluir un bloque de función de transferencia en esa rama, pero su valor sería simplemente 1, por lo que es una práctica estándar omitir ese bloque obvio.

   

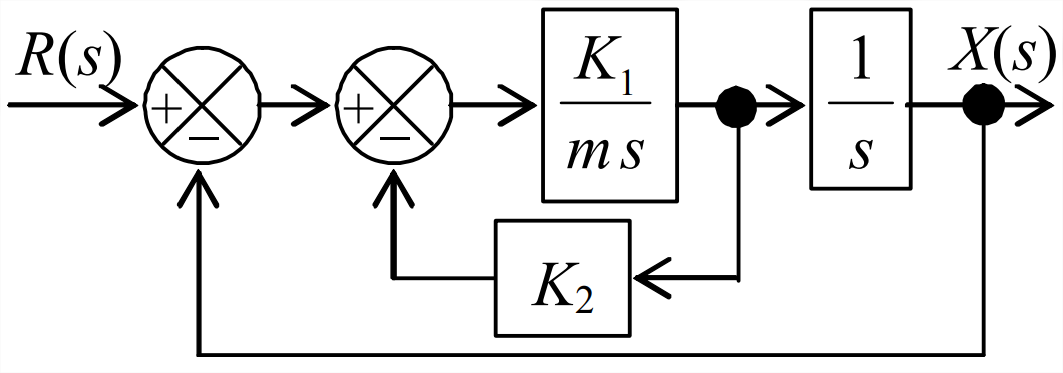
   Figura\(\PageIndex{8}\) (Copyright; autor vía fuente)

   1. Utilice el resultado del Problema 14.3 o cualquier otro método de su elección para mostrar que la función de transferencia de bucle cerrado es\[\frac{X(s)}{R(s)}=\frac{K_{1}}{m s^{2}+K_{1} K_{2} s+K_{1}} \nonumber \]
   2. Supongamos que los CI son cero y que la entrada a este sistema es una función de paso,\(r(t) = R_{H} H(t)\). Para el (los) caso (s) asignado (s), el valor del parámetro de tipo masa\(m\) (en unidades consistentes) se da en la columna 2 de la siguiente tabla. Calcular los valores de constantes\(K_1\) y\(K_2\) (en unidades consistentes) que producirán los valores de relación máxima de sobreimpulso\(\bar{x}_{p}\) y tiempo pico dados en las columnas 3 y 4 de la tabla (ver Sección 9.8). Tenga en cuenta que este es un ejercicio de diseño: está calculando valores de parámetros del sistema que están destinados a producir objetivos de control especificados. Completa el problema calculando también el tiempo de subida\(t_r\) y el tiempo de asentamiento\(t_s\). Las respuestas parciales se dan en las columnas 5 y 6 de la tabla a continuación para ayudarle a saber si está, o no está en el camino correcto, pero aún debe mostrar todas las derivaciones y cálculos que conduzcan a estas respuestas.
   3. Que la magnitud del paso de la parte 14.7.2 sea\(R_{H}=0.753\) (en unidades consistentes). Calcule el valor final\(\lim _{t \rightarrow \infty} x(t)\), después de que todo el movimiento dinámico se haya amortiguado.