15.2: Ejemplos de P y PI Control

La figura\(\PageIndex{1}\) de la siguiente página representa una planta mecánica que es apropiada para ilustrar el control P y el control PI. Un rotor ligero se sumerge en un líquido viscoso, de manera que el momento de amortiguación impuesto sobre el rotor es\(-c_{\theta} \dot{\theta}\). El rotor está unido al dispositivo mecánico de ajuste del operador (una rueda de control, por ejemplo) a través de un resorte de torsión altamente flexible que tiene constante de rigidez rotacional\(k_{\theta}\). El rotor tiene una inercia rotacional suficientemente baja\(J\), y la constante de amortiguación viscosa\(c_{\theta}\) es suficientemente grande, lo que suponemos que el momento\(-J \ddot{\theta}\) inercial es insignificante en comparación con los momentos de amortiguación y estructurales.

Figura\(\PageIndex{1}\): Rotor ligero sumergido en un líquido viscoso, con conexión a la entrada a través de un muelle de torsión suave. (Copyright; autor vía fuente)

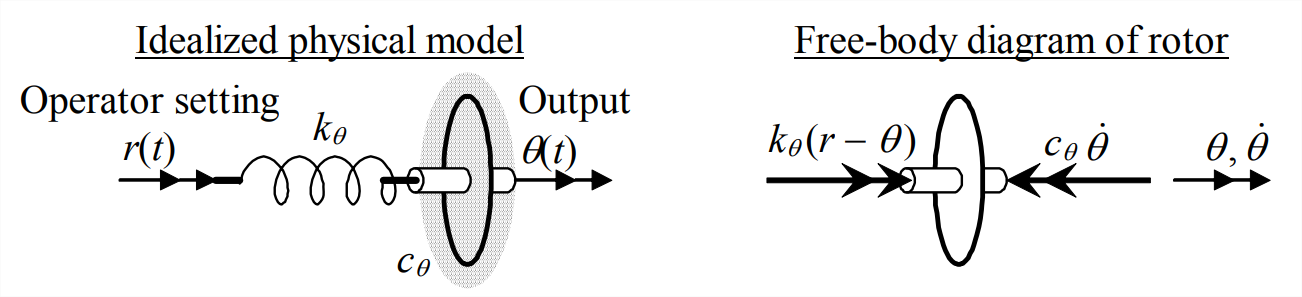
La ecuación de movimiento proviene del FBD en la Figura\(\PageIndex{1}\):

\[k_{\theta}(r-\theta)-c_{\theta} \dot{\theta}=J \ddot{\theta} \approx 0 \Rightarrow \frac{c_{\theta}}{k_{\theta}} \dot{\theta}+\theta=r \Rightarrow \tau_{1} \dot{\theta}+\theta=r(t), \text { where } \tau_{1}=\frac{c_{\theta}}{k_{\theta}}\label{eqn:15.4} \]

Tomando la transformada de Laplace de Ecuación\(\ref{eqn:15.4}\) da la función básica de transferencia de planta:

\[\operatorname{PTF}(s)=\frac{L[\theta(t)]}{L[r(t)]} \equiv \frac{\Theta(s)}{R(s)}=\frac{1}{\tau_{1} s+1}\label{eqn:15.5} \]

Claramente, esta planta mecánica idealizada de bucle abierto por sí misma es un sistema simple de ^primer orden con constante de tiempo\(\tau_{1}=c_{\theta} / k_{\theta}\); además, este sistema es el equivalente rotacional del filtro de paso bajo amortiguador-resorte de la serie traslacional descrito en la Figura 3.7.4 y la Ecuación 3.7.5.

La entrada a la planta es el ángulo\(r(t)\) de ajuste del operador y la salida es la posición del rotor\(\theta(t)\). De la ecuación ODE\(\ref{eqn:15.4}\), vemos que la salida pseudo-estática es exactamente igual a la entrada,\(\theta_{p s}(t)=r(t)\). Entonces, especifiquemos que nuestro objetivo de control para este sistema es hacer que la salida real\(\theta(t)\) esté lo más cerca posible de la entrada\(r(t)\). Para desarrollar una sensación física por el comportamiento de la planta de bucle abierto en la Figura\(\PageIndex{1}\), supongamos que el operador mueve rápidamente la rueda de control hacia un lado para que la entrada\(r(t)\) esté cerca de una función de paso. El resorte de torsión se enrollará inmediatamente con más fuerza, e impondrá un momento sobre el rotor. Sin embargo, como podemos visualizar intuitivamente, la restricción viscosa sobre el rotor evitará que se mueva tan rápido como la entrada, y el ángulo del rotor retardará la entrada. A medida que pasa el tiempo y el resorte de torsión se desenrolla gradualmente, el ángulo del rotor eventualmente se asentará en el ángulo de entrada.

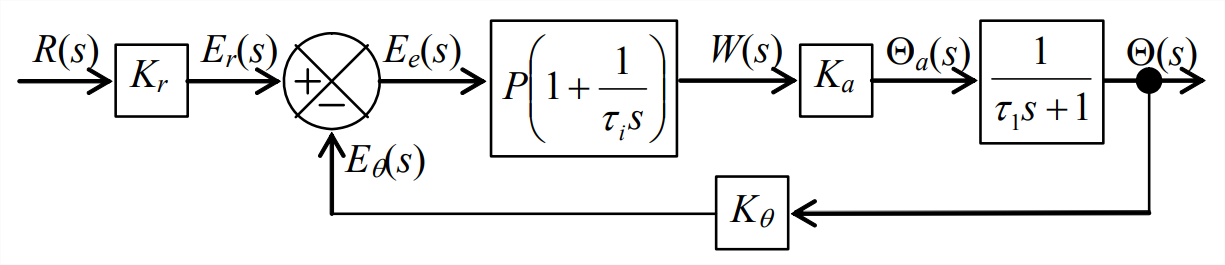
Supongamos que la respuesta de bucle abierto es demasiado lenta para nuestros propósitos, y que queremos acelerar la respuesta mediante el uso de sensores, un actuador, retroalimentación y control P o PI en el sistema representado en la página siguiente, en forma funcional en la Figura\(\PageIndex{2}\), y como un diagrama de bloques de Laplace correspondiente en la Figura \(\PageIndex{3}\). La función de transferencia en la Figura\(\PageIndex{3}\) para el controlador P o PI proviene de la Ecuación 15.1.2, y la función de transferencia para la planta de rotor-resorte-líquido proviene de la Ecuación\(\ref{eqn:15.5}\). El transductor de entrada y el sensor de posición de salida mostrados en las Figuras\(\PageIndex{2}\) y\(\PageIndex{3}\) son familiares del Capítulo 14 (en la Figura 14.3.1, por ejemplo). Pero el “actuador de posición” es algo nuevo. Mientras que la salida de la mayoría de los motores es el par, la salida de este actuador de posición se especifica como posición rotacional. Para que un actuador se comporte de esta manera se requiere un sistema de control de retroalimentación dentro del propio actuador; esta es una característica de los sistemas de control que ahora hacemos una pausa para examinar.

Figura\(\PageIndex{2}\): Diagrama funcional de un sistema para controlar la posición de un rotor conectado por resorte en un líquido viscoso, basado en un control proporcional-integral. (Copyright; autor vía fuente)

Figura\(\PageIndex{3}\): Diagrama de bloques de Laplace de un sistema para controlar la posición de un rotor conectado por resorte en un líquido viscoso, basado en proporcional-integral. (Copyright; autor vía fuente)

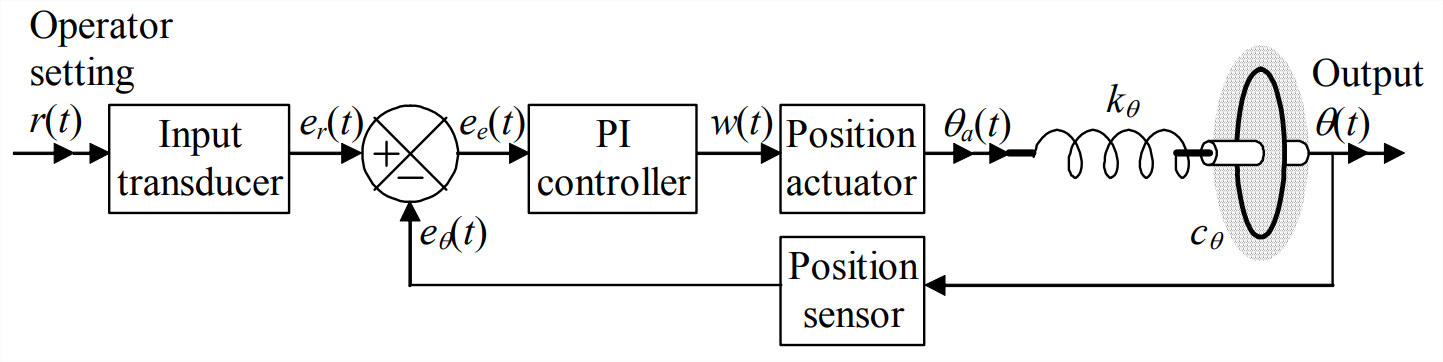
De hecho, la mayoría de los actuadores y sensores de todo tipo son en sí mismos sistemas dinámicos complicados, a menudo con circuitos de retroalimentación internos. Pero esto plantea la siguiente pregunta: si hay sistemas de control dentro de los actuadores y/o sensores, entonces ¿por qué no se incluyen los detalles de estos sistemas en las funciones de transferencia del dispositivo o subsistema que se muestran en diagramas de bloques como la Figura\(\PageIndex{3}\)?

Una respuesta general a esta pregunta se basa en las “velocidades” relativas de diferentes sistemas. Para ilustrar este concepto de velocidad del sistema, imaginamos que dos sistemas estándar de ^segundo orden, A y B, tienen valores equivalentes de relación de amortiguación viscosa subcrítica\(\zeta\), pero que la frecuencia natural no amortiguada del Sistema A es 100 veces mayor que la del Sistema B,\(\omega_{n A} / \omega_{n B} = 100\). En consecuencia, el tiempo de asentamiento del Sistema A para las entradas de paso,\(t_{s A}=4 /\left(\zeta \omega_{n A}\right)\) [Ecuación 9.8.11], es solo 0.01 el del Sistema B; en este caso, consideramos que “la dinámica del Sistema A” es “100 veces más rápida” que “la dinámica del Sistema B.” Los ingenieros suelen seleccionar para un sistema de control sensores ¹ y, cuando sea posible, actuadores que son mucho más rápidos que la dinámica de la planta bajo control; en tales casos, generalmente aproximamos el comportamiento de un sensor o actuador con una constante de sensibilidad lineal simple, en ecuaciones tales como\(e_{r}(t)=K_{r} r(t)\),\(e_{\theta}(t)=K_{\theta} \theta(t)\), y\(\theta_{a}(t)=K_{a} w(t)\), todos los cuales están representados en la Figura\(\PageIndex{3}\). En estos casos, estamos haciendo la aproximación de que las dinámicas de los sensores y actuadores son esencialmente infinitamente rápidas y son independientes de, o “desacopladas” de la dinámica de la planta.

Tenga en cuenta, sin embargo, que la dinámica completa de los dispositivos utilizados para el control, especialmente los actuadores, no siempre puede considerarse desacoplada de la dinámica de la planta. Por un ejemplo, las dinámicas de un actuador de reacción-masa (tarea Problema 10.15) en un sistema de control de vibraciones suelen estar inextricablemente acopladas con las de la planta estructural, como en la tarea Problema 12.6. Para otro ejemplo, tarea Problema 15.7 es un ejercicio de incorporar la dinámica de un actuador de posición en un modelo de sistema de control; en este caso, el proceso implica incluso más que simplemente insertar la función de transferencia del actuador en serie dentro del diagrama de bloques del sistema general. En otro ejemplo más, Dettmer, 1995, Sección 1.3.4 describe un sistema de control para el cual fue necesario dar cuenta de las características dinámicas tanto de sensores como de actuadores.

Volviendo ahora al sistema de control de posición de rotor de Figuras\(\PageIndex{2}\) y\(\PageIndex{3}\), nuestro objetivo es hacer que la salida siga la entrada\(\theta(t) \approx r(t)\), por lo que es apropiado definir una configuración de bucle abierto revisada (relativa a la Figura\(\PageIndex{1}\)). Si el bucle de retroalimentación en la Fig. 15- 5 se rompiera, y si el controlador PI no estuviera presente (\(P\)= 1,\(b_i\) = 0), entonces la función de transferencia para este sistema de bucle abierto claramente sería\(K_{r} \times K_{a} \times 1 /\left(\tau_{1} s+1\right)\). Queremos que esto sea lo mismo que el de la planta desnuda (desprovista de dispositivos de control), Ecuación\(\ref{eqn:15.5}\), así que supongamos que tenemos la capacidad de establecer las sensibilidades del transductor de entrada y el actuador de posición para que\(K_{r} \times K_{a}=1\). Además, simplificará enormemente el álgebra en los siguientes desarrollos si suponemos además que podemos usar sensores idénticos en el ángulo de entrada y el ángulo de salida en la ruta de retroalimentación, de manera que eso\(K_{r}=K_{\theta}\). Para resumir, aplicaremos las siguientes restricciones a las sensibilidades del dispositivo:

\[K_{r} \times K_{a}=1 \quad \text { and } \quad \frac{K_{\theta}}{K_{r}}=1\label{eqn:15.6} \]

Para comparar los rendimientos del sistema de bucle abierto y de bucle cerrado, consideremos la respuesta (desde cero condiciones iniciales) hasta la entrada por pasos\(r(t)=R_{H} H(t) \Rightarrow R(s)=R_{H} / s\). Luego, para el sistema de bucle abierto, el uso de la función de transferencia Ecuación\(\ref{eqn:15.5}\) y expansión de fracción parcial da

\[\Theta(s)=R_{H} \frac{1}{s} \frac{1}{\tau_{1} s+1}=R_{H}\left(\frac{1}{s}-\frac{1}{s+1 / \tau_{1}}\right)\label{eqn:15.7} \]

Tomando la transformada inversa de Laplace da la respuesta escalonada del sistema de bucle abierto:

\[\theta(t)=R_{H}\left(1-e^{-t / \tau_{1}}\right), \text { for } t \geq 0\label{eqn:15.8} \]

\(\ref{eqn:15.8}\)^{La ecuación es simple respuesta escalonada de primer orden del tipo que se muestra en la Figura 3.4.2.} Al final de esta sección, se realiza una evaluación numérica comparativa de esta respuesta de bucle abierto y respuestas escalonadas para los tipos P e PI de control de bucle cerrado. Por ahora, sin embargo, solo observemos a partir de la ecuación\(\ref{eqn:15.8}\) que el valor asintótico o “final” de respuesta por tiempos mucho mayores que la constante de tiempo\(\tau_{1}\) es igual a la magnitud de la entrada de paso, según sea necesario:

\[\lim _{t \rightarrow \infty} \theta(t)=R_{H}\label{eqn:15.9} \]

A continuación, analicemos el control proporcional (P) de bucle cerrado, para lo cual\(b_{i}=0\) en la Figura\(\PageIndex{3}\). Así, para el bucle cerrado de la Figura\(\PageIndex{3}\), tenemos para la Ecuación 14.4.6 los polinomios\(N_{G}=P \times K_{a}\)\(D_{G}=\tau_{1} s+1\),\(N_{H}=K_{\theta}\),\(D_{H}=1\), y, que usamos para encontrar lo siguiente\(CLTF(s)\):

\[\frac{\Theta(s)}{R(s)}=K_{r} \times \frac{N_{G} D_{H}}{D_{G} D_{H}+N_{G} N_{H}}=\frac{K_{r} P K_{a}}{\tau_{1} s+1+P K_{a} K_{\theta}}=K_{r} K_{a} \frac{P}{\tau_{1} s+1+K_{r} K_{a} \frac{K_{\theta}}{K_{r}} P} \nonumber \]

Con la simplificación de suposiciones Ecuación\(\ref{eqn:15.6}\), esto se convierte

\[C L T F(s)=\frac{\Theta(s)}{R(s)}=\frac{P}{\tau_{1} s+1+P}=\frac{P}{1+P} \frac{1}{\left(\frac{\tau_{1}}{1+P}\right) s+1} \equiv \frac{P}{1+P} \frac{1}{\tau_{1 P} s+1}\label{eqn:15.10} \]

en la que la nueva constante de tiempo para el sistema controlado proporcionalmente es

\[\tau_{1 P} \equiv \frac{\tau_{1}}{1+P}\label{eqn:15.11} \]

Para la entrada de pasos\(r(t)=R_{H} H(t) \Rightarrow R(s)=R_{H} / s\), la ecuación\(\ref{eqn:15.10}\) da la transformación

\[\Theta(s)=\frac{R_{H}}{s} \times C L T F(s)=R_{H} \frac{P}{1+P} \times \frac{1}{s} \frac{1}{\tau_{1 P} s+1}\label{eqn:15.12} \]

Por lo tanto, encontramos la respuesta escalonada del sistema controlado proporcionalmente simplemente comparando la Ecuación\(\ref{eqn:15.12}\) con la Ecuación\(\ref{eqn:15.7}\) y luego modificando la Ecuación\(\ref{eqn:15.8}\) apropiadamente:

\[\theta(t)=R_{H} \frac{P}{1+P}\left(1-e^{-t / \tau_{1} p}\right), \text { for } t \geq 0\label{eqn:15.13} \]

El valor asintótico o “final” de la respuesta escalonada controlada proporcionalmente para tiempos mucho mayores que la constante de tiempo\(\tau_{1 P}\) es:

\[\lim _{t \rightarrow \infty} \theta(t)=R_{H} \frac{P}{1+P}\label{eqn:15.14} \]

Esta situación brinda la oportunidad de introducir el teorema del valor final e ilustrar su aplicación; esta es una herramienta matemática útil que se deriva en la siguiente sección. Este teorema nos permite encontrar el valor asintótico finito de una función de tiempo\(f(t)\), asumiendo que tal valor existe, basado únicamente en la transformada de Laplace\(L[f(t)]=F(s)\), sin requerir que la ecuación para\(f(t)\) estar disponible:

\[\lim _{t \rightarrow \infty} f(t)=\lim _{s \rightarrow 0}[s F(s)]\label{eqn:15.15} \]

Para la respuesta escalonada del sistema controlado proporcionalmente, el teorema del valor final y la Ecuación\(\ref{eqn:15.12}\) dan

\[\lim _{t \rightarrow \infty} \theta(t)=\lim _{s \rightarrow 0} s \times \Theta(s)=\lim _{s \rightarrow 0}\left(s \times R_{H} \frac{P}{1+P} \frac{1}{s} \frac{1}{\tau_{1 P} s+1}\right)=\lim _{s \rightarrow 0}\left(R_{H} \frac{P}{1+P} \frac{1}{\tau_{1 P} s+1}\right)=R_{H} \frac{P}{1+P} \nonumber \]

Este es otro método más fácil para encontrar el resultado Ecuación\(\ref{eqn:15.14}\). El teorema del valor final no fue necesario para derivar la solución asintótica correcta para este simple caso, pero será una herramienta útil y ahorradora de mano de obra para casos más complicados en el futuro.

Comparando la Ecuación\(\ref{eqn:15.14}\) con el valor asintótico requerido\(\lim _{t \rightarrow \infty} \theta(t)=R_{H}\)\(\ref{eqn:15.9}\), Ecuación, vemos que\(P /(1+P) \neq 1\), porque, el sistema controlado proporcionalmente no satisface exactamente el requisito. Examinemos los posibles valores de ganancia proporcional\(P\). La ecuación\(\ref{eqn:15.11}\) requiere\(P>-1\) que para que el sistema sea estable,\(\tau_{1 P}>0\). \(\ref{eqn:15.13}\)La ecuación requiere\(P > 0\) eso para que la respuesta tenga el mismo signo que la entrada. Además,\(P\) debe ser un número positivo lo más grande posible, dentro de limitaciones prácticas de hardware, ya que

1. cuanto mayor sea el valor de\(P\), menor es la constante de tiempo\(\tau_{1 P}\), lo que hace que el sistema sea más rápido que el sistema de bucle abierto, y
2. cuanto mayor sea el valor de\(P\), más cerca está el valor asintótico de la salida al valor de la entrada, de la Ecuación\(\ref{eqn:15.14}\).

El valor\(P = 4\) es una ganancia proporcional de uso común. Pero incluso para un valor grande y positivo de\(P\), la respuesta en estado estacionario será al menos un poco menor que la entrada. El error de salida en estado estacionario, también conocido como desplazamiento, se define como

\[\Delta \theta_{\text {offeet}} \equiv R_{H}-R_{H} \frac{P}{1+P}=\frac{R_{H}}{1+P}\label{eqn:15.16} \]

Se requiere un gran valor\(P > 9\),, para reducir el desplazamiento a menos del 10% de la salida de estado estacionario deseada.

Existe una explicación simple para el desplazamiento producido por el control proporcional (P), lo que también sugerirá un remedio. Los diagramas de bloques Figura\(\PageIndex{2}\) y Figura\(\PageIndex{3}\) muestran que el valor final de\(\theta_{a}\) debe ser distinto de cero, igual al valor final de salida\(\theta\). Es decir, el resorte de torsión debe estar completamente relajado (descargado) al final del proceso de control, lo cual es obvio físicamente. Además, trazando hacia atrás en las ramas hacia adelante de los bucles en Figuras\(\PageIndex{2}\) y\(\PageIndex{3}\), encontramos los otros valores finales relevantes:\(w=\theta_{a} / K_{a}=\theta / K_{a}\), y, con\(b_{i}=0\),\(e_{e}=w / P=\theta_{a} /\left(K_{a} P\right)=\theta /\left(K_{a} P\right) \neq 0\). Idealmente, la señal de error final\(e_{e}=e_{r}-e_{\theta}\) debería ser cero, correspondiendo a que la salida sea exactamente el valor final deseado; sin embargo, el argumento anterior muestra que el error final para el control P por sí solo es inevitablemente distinto de cero. Este argumento también sugiere que buscamos alguna manera de hacer que el error final sea igual a cero,\(e_{e}=0\), pero aún así preservar la entrada distinta de cero en el actuador de posición,\(w \neq 0\), de modo que\(\theta_{a} \neq 0\), y para que la salida final sea igual al valor deseado,\(\theta=r\). La acción integral (I) puede producir este efecto: si agregamos un término a\(w\) eso es proporcional a la integral de la señal de error\(\int_{\tau=0}^{\tau=t} e_{e}(\tau) d \tau\), entonces podemos tener una señal de control final distinta de cero,\(w \neq 0\), aunque el error final en sí sea cero,\(e_{e}=0\).

Por lo tanto, encontremos a continuación la función de transferencia de bucle cerrado para el control proporcional-integral (PI) de bucle cerrado (\(b_{i}=1\)). Para el bucle cerrado en la Figura\(\PageIndex{3}\), la función de transferencia de rama directa es\(G=P\left(1+\frac{1}{\tau_{i} s}\right) \times K_{a} \times \frac{1}{\tau_{1} s+1}=\frac{P K_{a}\left(\tau_{i} s+1\right)}{\tau_{i} s\left(\tau_{1} s+1\right)}\), así\(N_{G}=P K_{a}\left(\tau_{i} s+1\right)\) y\(D_{G}=\tau_{i} s\left(\tau_{1} s+1\right)\). Para la rama de retroalimentación,\(N_{H}=K_{\theta}\) y\(D_{H}=1\). Por lo tanto, la Ecuación 14.4.6 da lo siguiente\(CLTF(s)\)):

\ [\ begin {alineado}
\ frac {\ Theta (s)} {R (s)} &=K_ {r}\ veces\ frac {N_ {G} D_ {H}} {D_ {G} D_ {H} +N_ {G} N_ {H}} =\ frac {K_ {r} P K_ {a}\ izquierda (\ tau_ {i} s+1\ derecha)} {\ tau_ {i} s\ izquierda (\ tau_ {1} s+1\ derecha) +P K_ {a}\ izquierda (\ tau_ {i} s+1\ derecha) K_ {\ theta}}\\
&=K_ {r} K_ {a}\ frac {P\ izquierda (\ tau_ {i} s+1\ derecha) } {\ tau_ {i} s\ izquierda (\ tau_ {1} s+1\ derecha) +K_ {r} K_ {a}\ frac {K_ {\ theta}} {K_ {r}} P\ izquierda (\ tau_ {i} s+1\ derecha)}
\ end {alineado}\ nonumber\]

Con la simplificación de suposiciones Ecuación\(\ref{eqn:15.6}\), esto se convierte

\[\frac{\Theta(s)}{R(s)}=\frac{P\left(\tau_{i} s+1\right)}{\tau_{i} s\left(\tau_{1} s+1\right)+P\left(\tau_{i} s+1\right)}=\frac{P\left(\tau_{i} s+1\right)}{\tau_{i} \tau_{1} s^{2}+(1+P) \tau_{i} s+P}\label{eqn:15.17} \]

Antes de analizar la Ecuación con más\(\ref{eqn:15.17}\) detalle, primero determinemos si, como se predijo anteriormente, el control PI elimina el desplazamiento del control P de la Ecuación\(\ref{eqn:15.16}\). Para la entrada de pasos\(r(t)=R_{H} H(t) \Rightarrow R(s)=R_{H} / s\), la ecuación\(\ref{eqn:15.17}\) da la transformación

\[\Theta(s)=\frac{R_{H}}{s} \frac{P\left(\tau_{i} s+1\right)}{\tau_{i} s\left(\tau_{1} s+1\right)+P\left(\tau_{i} s+1\right)}\label{eqn:15.18} \]

Aplicando teorema de valor final Ecuación\(\ref{eqn:15.15}\) a Ecuación\(\ref{eqn:15.18}\) da

\[\lim _{t \rightarrow \infty} \theta(t)=\lim _{s \rightarrow 0} s \times \Theta(s)=\lim _{s \rightarrow 0}\left(\frac{R_{H} P\left(\tau_{i} s+1\right)}{\tau_{i} s\left(\tau_{1} s+1\right)+P\left(\tau_{i} s+1\right)}\right)=\lim _{s \rightarrow 0}\left(R_{H} \frac{P}{P}\right)=R_{H}\label{eqn:15.19} \]

Por lo tanto, la acción integral efectivamente elimina el error que es inevitable del control puramente proporcional.

Volviendo a la ecuación de la función de transferencia\(\ref{eqn:15.17}\), vemos que la acción integral ha aumentado el orden del sistema a ^2º orden desde el ^primer orden de la planta. En consecuencia, podemos reescribir la función de transferencia en términos de parámetros apropiados para un sistema ^{de segundo} orden:

\[\frac{\Theta(s)}{R(s)}=\frac{\frac{P}{\tau_{i} \tau_{1}}\left(\tau_{i} s+1\right)}{s^{2}+\frac{1+P}{\tau_{1}} s+\frac{P}{\tau_{i} \tau_{1}}} \equiv \frac{\omega_{n}^{2}\left(\tau_{i} s+1\right)}{s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}}\label{eqn:15.20} \]

en el que la frecuencia natural no amortiguada y la relación de amortiguación viscosa son, respectivamente,

\[\omega_{n}=\sqrt{\frac{P}{\tau_{i} \tau_{1}}} \text { and } \zeta=\frac{1}{2 \omega_{n}} \frac{1+P}{\tau_{1}}=\frac{1}{2} \sqrt{\frac{\tau_{i}}{\tau_{1}}} \frac{1+P}{\sqrt{P}}\label{eqn:15.21} \]

Obsérvese que este sistema no es un sistema estándar ^{de segundo} orden, como se define en la Ecuación 9.2.2. El término\(\omega_{n}^{2} \tau_{i} s\) en el numerador de Ecuación\(\ref{eqn:15.20}\) hace que este sistema no sea estándar; ese término corresponde a la dinámica del lado derecho en la ODE describiendo el sistema, que es\(\ddot{\theta}+2 \zeta \omega_{n} \dot{\theta}+\omega_{n}^{2} \theta=\omega_{n}^{2}\left(\tau_{i} \dot{r}+r\right)\). El carácter no estándar significa, entre otras cosas, que las especificaciones de respuesta escalonada derivadas en la Sección 9.8 no se aplican exactamente para este sistema.

Para la comparación con los casos anteriores de control de bucle abierto y P, resolvamos la respuesta del sistema controlado por PI a la entrada por pasos\(r(t)=R_{H} H(t) \Rightarrow R(s)=R_{H} / s\). La ecuación\(\ref{eqn:15.20}\) da la transformación

\[\Theta(s)=\frac{R_{H}}{s} \frac{\omega_{n}^{2}\left(\tau_{i} s+1\right)}{s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}}=R_{H}\left[\frac{\omega_{n}^{2} \tau_{i}}{\omega_{d}} \frac{\omega_{d}}{\left(s+\zeta \omega_{n}\right)^{2}+\omega_{d}^{2}}+\frac{1}{s} \frac{\omega_{n}^{2}}{\left(s+\zeta \omega_{n}\right)^{2}+\omega_{d}^{2}}\right]\label{eqn:15.22} \]

La segunda forma de Ecuación\(\ref{eqn:15.22}\) se escribe sujeta a la condición\(|\zeta|<1\), de manera que\(\omega_{d}^{2} \equiv\omega_{n}^{2}\left(1-\zeta^{2}\right)>0\); ya que\(\zeta>0\) a partir de la Ecuación\(\ref{eqn:15.21}\), esto significa que asumimos que el sistema está subamortiguado, al menos inicialmente. Con Ecuación\(\ref{eqn:15.22}\) en la segunda forma, podemos aplicar las siguientes transformaciones inversas de Laplace. Primero, las Ecuaciones 9.3.5, 9.3.8 y 9.3.9 dan:

\[L^{-1}\left[\frac{\omega_{d}}{\left(s+\zeta \omega_{n}\right)^{2}+\omega_{d}^{2}}\right]=e^{-\zeta \omega_{n} t} \sin \omega_{d} t\label{eqn:15.23} \]

A continuación, las Ecuaciones 9.3.5 y 9.6.5 dan (ver tarea Problema 9.12):

\[L^{-1}\left[\frac{1}{s} \frac{\omega_{n}^{2}}{\left(s+\zeta \omega_{n}\right)^{2}+\omega_{d}^{2}}\right]=1-e^{-\zeta \omega_{n} t}\left(\cos \omega_{d} t+\frac{\zeta \omega_{n}}{\omega_{d}} \sin \omega_{d} t\right)\label{eqn:15.24} \]

Sustituir la ecuación\(\ref{eqn:15.23}\) y la ecuación\(\ref{eqn:15.24}\) en la transformada inversa de la ecuación\(\ref{eqn:15.22}\), luego combinar términos apropiadamente, da la respuesta escalonada del sistema bajo amortiguado controlado por PI:

\[\theta(t)=R_{H}\left[1-e^{-\zeta \omega_{n} t}\left(\cos \omega_{d} t+\frac{\zeta \omega_{n}-\omega_{n}^{2} \tau_{i}}{\omega_{d}} \sin \omega_{d} t\right)\right], \text { for } 0 \leq \zeta<1 \text { and } 0 \leq t\label{eqn:15.25} \]

En el ejemplo numérico a seguir, encontraremos casos tanto de subamortiguación como de sobreamortiguación; por lo tanto, es apropiado aplicar la ecuación de conversión 9.10.2 a la ecuación de respuesta subamortiguada\(\ref{eqn:15.25}\) Ecuación para escribir la siguiente ecuación para la respuesta escalonada de la ecuación controlada por PI sistema sobreamortiguado:

\[\theta(t)=R_{H}\left[1-e^{-\zeta \omega_{n} t}\left(\cosh \mu_{d} t+\frac{\zeta \omega_{n}-\omega_{n}^{2} \tau_{i}}{\mu_{d}} \sinh \mu_{d} t\right)\right], \text { for } 1<\zeta \text { and } 0 \leq t\label{eqn:15.26} \]

en el que\(\mu_{d}=\omega_{d} \sqrt{\zeta^{2}-1}\).

Ahora que hemos derivado las ecuaciones para la respuesta escalonada, evaluemos un caso numérico con parámetros físicamente plausibles; en particular, calculemos y comparemos las respuestas escalonadas: Ecuación\(\ref{eqn:15.8}\) para el sistema de bucle abierto; Ecuación\(\ref{eqn:15.13}\) para el sistema controlado por P; y Ecuación\(\ref{eqn:15.25}\) o Ecuación\(\ref{eqn:15.26}\) para el sistema controlado por PI. Dejamos que la constante de tiempo del sistema de bucle abierto tenga el valor\(c_{\theta} / k_{\theta} \equiv \tau_{1}=1\) s, y usamos el valor típico\(P = 4\) para la ganancia proporcional. Para el sistema controlado por PI, consideramos tres constantes de tiempo integrales diferentes,\(\tau_{i}=\) 1/3, 2/3 y 1 s. El siguiente es un archivo M de MATLAB que calcula las respuestas de paso y las traza en una sola gráfica:

%Matlabdemo151.m

%Sistema de primer orden: rotor conectado por resorte en un fluido viscoso

% de respuestas de paso: bucle abierto, controlado por P y controlado por PI

t=0:. 01:4;

tau1=1;% constante de tiempo del sistema de bucle abierto = 1 seg

Thol=1-exp (-t/tau1);% de relación de respuesta de paso de bucle abierto

P=4; Tau1P=tau1/ (1+P);

THP=p/ (1+P) * (1-exp (-t/Tau1P));% de relación de respuesta escalonada, P control

parcela (t, tHol, t, ThP), mantener

taui= [1/3 2/3 1];% de relaciones de respuesta escalonada, tres casos de control IP

para ni= 1:3,

wn=sqrt (P/ (taui (ni) *tau1)); zeta= (1+P)/(2*wn*tau1);

sig=zeta*wn; caso_taui_zeta= [ni taui (ni) zeta]

si zeta < 1

wd=wn*sqrt (1-zeta^2);

ThPi (ni,:) =1-exp (-sig*t). * (cos (wd*t) + (sig-wn^2*taui (ni)) /wd*sin (wd*t));

else

md=wn*sqrt (zeta^2-1);

ThPi (ni,:) =1-exp (-sig*t). * (cosh (md*t) + (sig-wn^2*taui (ni)) /md*sinh (md*t));

final

parcela (t, ThPi (ni,:), 'k')

final

grid, xlabel ('Tiempo t (seg) '), ylabel ('Relación de respuesta de paso\ theta (t) /R_H')

title ('Control de posición de un rotor conectado por resorte en un fluido viscoso')

El comando MATLAB y la salida resultante se imprimen a continuación. Los tres casos mostrados son para el control PI con constante de tiempo integral (“taui”)\(\tau_i\) = 1/3, 2/3 y 1 seg; anotar los valores de relación de amortiguación viscosa (“zeta”)\(\zeta\): el sistema está subamortiguado por\(\tau_i\) = 1/3 s, pero sobreamortiguado para\(\tau_i\) = 2/3 y 1 s.

>> MatlabDemo151

Parcela actual mantenida

caso_taui_zeta =

1.0000 0.3333 0.7217

caso_taui_zeta =

2.0000 0.6667 1.0206

caso_taui_zeta =

3.0000 1.0000 1.2500

La figura\(\PageIndex{4}\) es la salida gráfica del archivo M de MATLAB.

Figura\(\PageIndex{4}\): Respuestas escalonadas para control sin control (bucle abierto), control proporcional (P) y control proporcional-integral (PI). (Copyright; autor vía fuente)

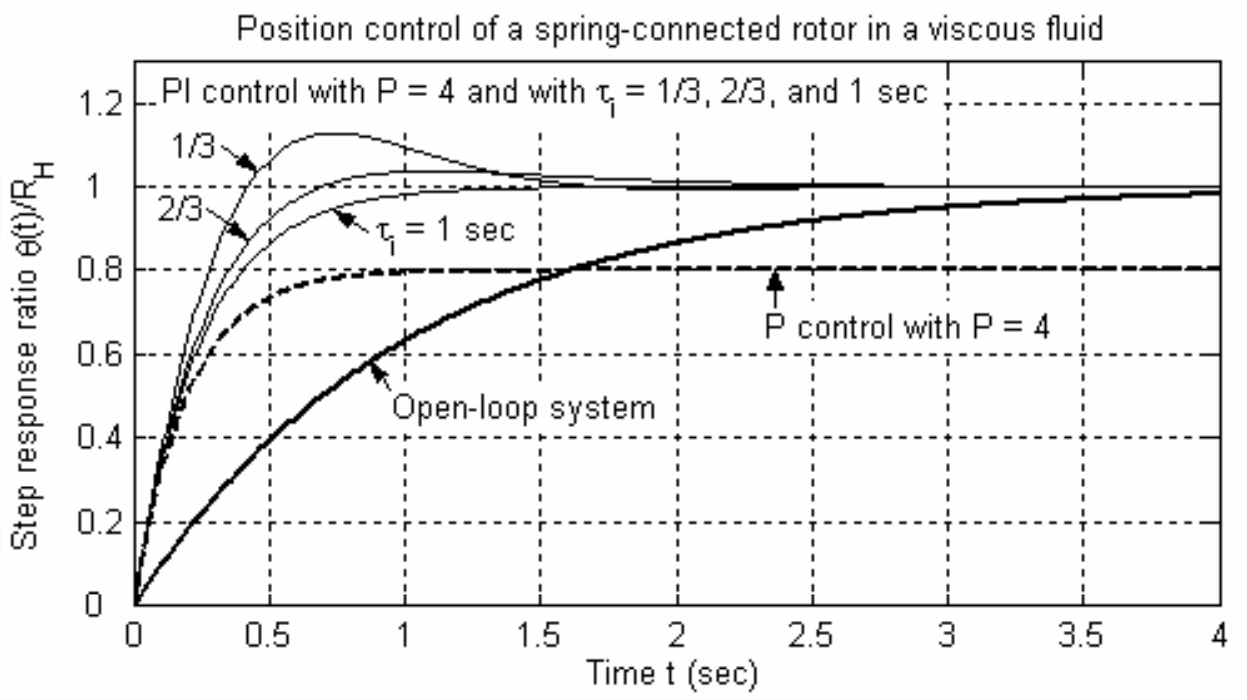
La figura\(\PageIndex{4}\) ilustra claramente los resultados obtenidos previamente con respecto a las constantes de tiempo para el control de bucle abierto y P, y los valores finales de respuesta escalonada para bucle abierto, control P y control PI. Los nuevos e interesantes resultados de la Figura\(\PageIndex{4}\) se relacionan con la respuesta escalonada del sistema bajo control de PI. Para los tres valores de\(\tau_{i}\), la velocidad de respuesta es mucho más rápida que la del sistema de bucle abierto, y comparable a la del control P. Además, existe una compensación de diseño para este sistema de ^segundo orden entre el tiempo de subida y el sobreimpulso. Recordemos de la Sección 9.8 que el tiempo de subida es el tiempo requerido para que la respuesta primero alcance el valor deseado, y el sobreimpulso es la cantidad máxima en la que la respuesta excede el valor deseado. Para la mayoría de los casos, al diseñador de control le gustaría hacer que el tiempo de subida sea lo más rápido posible y minimizar el sobreimpulso. No obstante, la Figura\(\PageIndex{4}\) muestra que no podemos hacer ambas cosas simultáneamente en este caso: el tiempo de subida es el más rápido para los pequeños\(\tau_{i}\), pero el sobreimpulso se minimiza o se elimina con mayores\(\tau_{i}\). Por lo tanto, el diseñador de control debe comprometer y seleccionar un valor\(\tau_{i}\) que produzca valores prácticamente aceptables tanto de tiempo de subida como de sobreimpulso, aunque ninguno de los parámetros de respuesta sería el mejor posible.

Es interesante observar también de la Figura\(\PageIndex{4}\) que, para este sistema no estándar de ^segundo orden, hay sobreimpulso para\(\tau_{i}\) = 2/3 s\(\Rightarrow \zeta\) = 1.02; en otras palabras, hay sobreimpulso a pesar de que el sistema está sobreamortiguado. Esto es diferente de la respuesta escalonada de un sistema de ^segundo orden estándar amortiguado positivamente (Sección 9.8), para lo cual el sobreimpulso puede ocurrir solo si\(0 \leq \zeta<1\).

¹ Ejemplos que aparecen en este libro de tales sensores son el acelerómetro [tarea Problema 10.12.2], el giroscopio de tasa (Ejemplo 9.2.2 en la Sección 9.2, y tarea Problema 9.18), y el giroscopio de integración de tasa (tarea Problema 9.19).