15.5: Capítulo 15 Tarea

1. Considere la función de transferencia de bucle cerrado Ecuación 15.4.3, con definiciones Ecuación 15.4.4, para el control de posición de un rotor mediante un controlador PD ideal.
   1. Supongamos que conocemos la inercia\(J\) rotacional\(K_{a}\), la sensibilidad del actuador y las sensibilidades iguales del transductor de entrada y retroalimentación\(K_{r}=K_{\theta}\), y que queremos especificar (es decir, “diseñar”) la frecuencia natural no amortiguada\(\omega_{n}\) y la relación de amortiguación viscosa\(\zeta\) para este sistema controlado. Por lo tanto, necesitamos determinar los valores apropiados para la ganancia proporcional\(P\) y la constante de tiempo derivada\(\tau_{d}\), que estableceríamos en el controlador PD. Para un sistema en particular, tenemos\(J=2.56 \mathrm{e}-3\) lb-s de ² pulgadas (el valor para una rueda de aluminio pequeña de aproximadamente cuatro pulgadas de diámetro, Figura 3.3.1), y el producto\(K_{r} K_{a}=0.0350\) lb-inch/rad; especifiquemos\(f_{n}=\omega_{n} / 2 \pi=1.00\) Hz (para que el tiempo de aumento de respuesta escalonada sea alrededor de ¼ s) y\(\zeta=+0.1\) (demasiado bajo para sistemas de control más prácticos, pero se adapta a los propósitos generales de este problema). Calcular los valores requeridos de\(P\) y\(\tau_{d}\) (s).
   2. Utilice la operación de residuo MATLAB (ver tarea Problema 2.15) para expandir la función de transferencia [con los valores numéricos de la parte 15.1.1] en una expansión de fracción parcial. Los polos son críticos para la estabilidad de cualquier sistema, que es el tema del Capítulo 16. Para este sistema, se debe encontrar un par de polos que son conjugados complejos, y su parte real debe ser negativa, esto significa que el sistema es estable.
   3. Que la entrada sea un paso,\(r(t)=R_{H} H(t)\). Primero, aplicar el teorema del valor final para encontrar\(\lim _{t \rightarrow \infty} \theta(t)\). A continuación, use transformaciones inversas Ecuaciones 15.2.22 y 15.2.23 [o simplemente adapte adecuadamente la ecuación de respuesta de paso 15.2.24 a este caso] para mostrar que la respuesta de paso es\[\theta(t)=R_{H}\left[1-e^{-\zeta \omega_{n} t}\left(\cos \omega_{d} t-\frac{\zeta \omega_{n}}{\omega_{d}} \sin \omega_{d} t\right)\right], \text { for }|\zeta|<1 \text { and } \omega_{d}=\omega_{n} \sqrt{1-\zeta^{2}} \nonumber \] Finalmente, deje que la magnitud del paso de entrada sea\(R_{H}=0.1\) radián, con los valores numéricos de la parte 15.1.1, y use MATLAB para trazar la salida \(\theta(t)\)en el intervalo de tiempo 0-2.5 s, aproximadamente 2½ ciclos.
   4. Para simular lo que pasaría si cometiste un error y obtuviste la señal equivocada para\(\tau_{d}\) (y por lo tanto para\(\zeta\))\(\zeta=-0.1\), deja, y repite las operaciones de las partes 15.1.2 y 15.1.3. Si puedes trazar\(\theta(t)\) para ambos\(\zeta=+0.1\) y\(\zeta=-0.1\) en la misma gráfica, mejorará la comparación de los dos casos. Porque\(\zeta=-0.1\), se debe encontrar que la parte real de los polos conjugados complejos es positiva; el historial de tiempo asociado\(\theta(t)\) debe indicar sistema en estabilidad. Observe para este sistema inestable que el teorema del valor final predice incorrectamente un valor de estado estacionario finito para esta respuesta escalonada.
2. Considera el control PID ideal de la posición de un rotor que tenga inercia significativa\(J\). Demos cuenta también de un momento de perturbación\(M_{d}(t)\) que actúa sobre el rotor. El diagrama de bloques de Laplace para este sistema ^{de tercer} orden se dibuja arriba. En los siguientes ejercicios, supongamos que este sistema es estable.

   

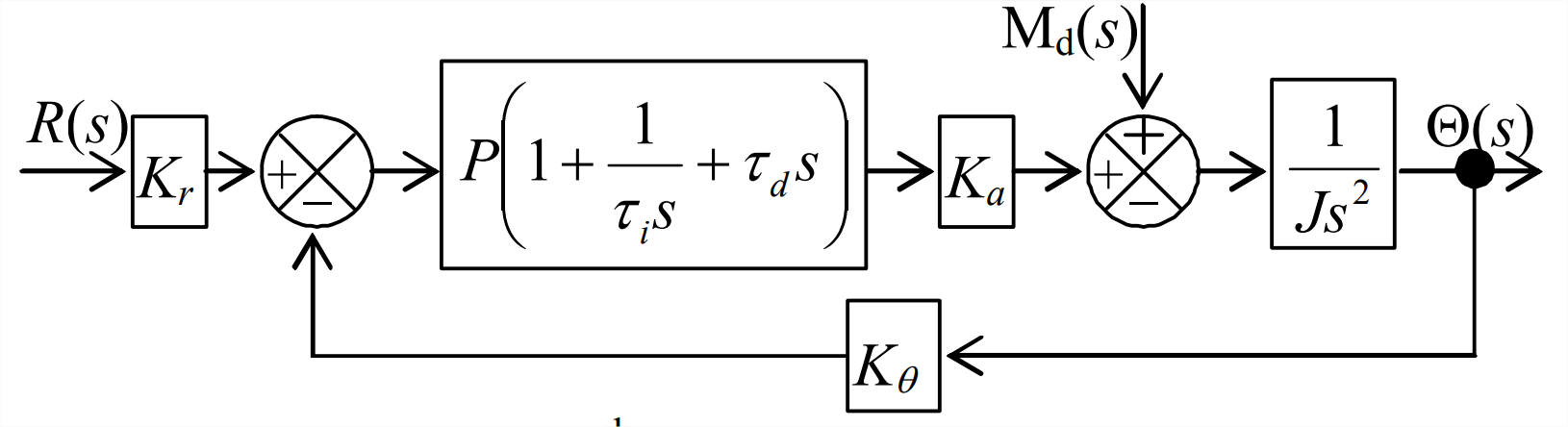
   Figura\(\PageIndex{1}\) (Copyright; autor vía fuente)

   1. Para la perturbación cero\(\mathrm{M}_{\mathrm{d}}(s)=0\),, derivar la ecuación algebraica para la función de transferencia de bucle cerrado\(\Theta(s) / R(s)\). Para entrada paso,\(r(t)=R_{H} H(t)\), aplicar el teorema del valor final para encontrar\(\lim _{t \rightarrow \infty} \theta(t)\).
   2. Para entrada cero,\(R(s)=0\), derivar la ecuación algebraica para la función de transferencia de bucle cerrado\(\Theta(s) / \mathrm{M}_{\mathrm{d}}(s)\). Para perturbación escalonada\(M_{d}(t)=M_{H} H(t)\),, aplicar el teorema del valor final para encontrar\(\lim _{t \rightarrow \infty} \theta(t)\). Un sistema de control debe suprimir la salida permanente debido a una perturbación escalonada.
3. Considera el control PI de la velocidad (no posición) de un rotor que tenga inercia significativa\(J\). El sensor en la salida es un tacómetro con ganancia constante\(K_p\), por lo que la señal eléctrica que se retroalimenta es\(K_{p} \dot{\theta}\). (Esta configuración ilustra una regla general en el diseño del sistema de control: detectar y retroalimentar la cantidad que desea controlar). Se trata de un modelo simplificado, por ejemplo, del sistema de control de crucero de un automóvil. Permitamos también un momento de perturbación\(M_{d}(t)\) actuando sobre el rotor. El diagrama de bloques de Laplace para este sistema está a la izquierda.

   

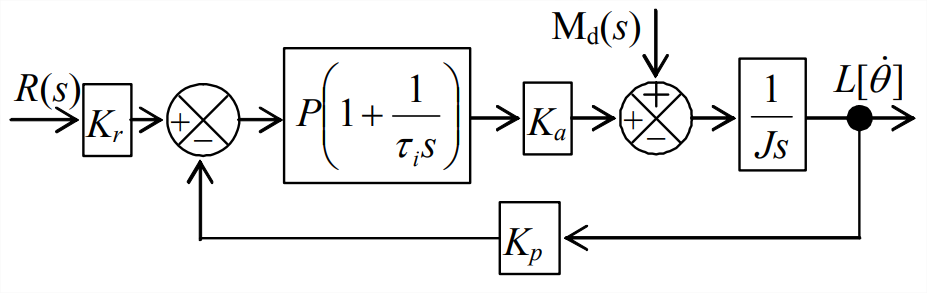
   Figura\(\PageIndex{2}\) (Copyright; autor vía fuente)

   1. Para la perturbación cero,\(\mathrm{M}_{\mathrm{d}}(s)=0\), derivar la ecuación algebraica en términos de todos los parámetros en el diagrama de bloques de Laplace para la función de transferencia de bucle cerrado\(L[\dot{\theta}] / R(s)\) que relaciona la velocidad de rotación de salida\(\dot{\theta}(t)\) con el comando de entrada\(r(t)\). Para la entrada por paso\(r(t)=R_{H} \times H(t)\),, aplique el teorema del valor final para encontrar la ecuación algebraica para\(\lim _{t \rightarrow \infty} \dot{\theta}(t)\), asumiendo que existe este valor asintótico. Explique (quizás usando un ejemplo de su propia experiencia, como un sistema de control de cruceros) la importancia física de la relación entre\(K_{r} / K_{p}\) la sensibilidad entrada-transductor y la sensibilidad del tacómetro.
   2. Derivar ecuaciones algebraicas para frecuencia natural no amortiguada\(\omega_{n}\) y relación\(\zeta\) de amortiguación viscosa de este sistema controlado, en términos de inercia\(J\), sensibilidad del actuador\(K_{a}\), sensibilidad del tacómetro\(K_{p}\)\(P\), ganancia proporcional y constante de tiempo integral\(\tau_{i}\).
4. En este problema, producirá gráficamente y comparará las funciones de frecuencia-respuesta del diferenciador exacto, pero físicamente irrealizable\(x_{d} \equiv \dot{e}_{e}\) (que se utiliza en este libro para el control ideal de PD) y un diferenciador aproximado, pero físicamente realizable que tiene el carácter de un filtro de paso alto.
   1. La sección 15.4 da la ODE del diferenciador aproximado como\(\varepsilon \tau_{d} \dot{x}_{d}+x_{d}=\dot{e}_{e}\),\(\tau_{d}\) siendo la constante de tiempo derivada positiva y\(\mathcal{E}\) siendo un número positivo pequeño en el rango 0.1-0.3; muestran que la función compleja frecuencia-respuesta (FRF) de la señal de salida\(x_{d}(t)\) relativa a la entrada la señal\(e_{e}(t)\) es\(F R F(\omega)=j \omega /\left(1+j \omega \varepsilon \tau_{d}\right)\).
   2. Para la respuesta de frecuencia, la señal de entrada tiene la forma sinusoidal de estado estacionario\(e_{e}(t)=E_{e} \cos \omega t\) y la señal de salida tiene la forma correspondiente\(x_{d}(t)=X_{d}(\omega) \cos (\omega t+\phi)\). Utilice la FRF de la parte 15.4.1 para mostrar que las ecuaciones para la relación de magnitud FRF y la fase del diferenciador aproximado son\(\frac{X_{d}(\omega)}{\omega_{b} E_{e}}=\frac{\bar{\omega}}{\sqrt{1+\bar{\omega}^{2}}}\) y\(\phi(\omega)=\frac{\pi}{2}-\tan ^{-1} \bar{\omega}\), en las que la frecuencia de ruptura es\(\omega_{b} \equiv 1 /\left(\varepsilon \tau_{d}\right)=2 \pi f_{b}\) y la relación de frecuencia adimensional es\(\bar{\omega} \equiv \omega / \omega_{b}=f / f_{b}\). Utilice la ecuación de relación de magnitud para derivar ecuaciones para las asíntotas de baja frecuencia y alta frecuencia, y esbozar esas asíntotas en una gráfica logarítmica como la Figura 4.3.3. El diferenciador aproximado debe exhibir el carácter de un filtro de paso alto, análogo al sistema de tarea Problema 4.4. Usa las asíntotas como envolvente para guiarte en el bosquejo de la curva real de\(X_{d}(\omega) /\left(\omega_{b} E_{e}\right)\), como se hace en la Figura 4.3.3. Finalmente, en una gráfica semilogarítmica debajo de la gráfica log-log (análoga a la Figura 4.3.2), esbozar la variación con frecuencia de fase\(\phi(\omega)\).
   3. Ahora considere el diferenciador exacto, con ecuación\(x_{d} \equiv \dot{e}_{e}\). Repita todos los pasos de las partes 15.4.1 y 15.4.2 para el diferenciador exacto, esbozando las curvas de relación magnitud y fase en las gráficas de la parte 15.4.2, pero en algún color o estilo de línea diferente, para que las curvas para diferenciadores exactos y aproximados sean claramente distinguibles. Debe ser capaz de inferir de estas gráficas finales los rangos de frecuencia sobre los cuales el diferenciador aproximado es razonablemente exacto, o inexacto.
5. Considere la función de transferencia de la posición del rotor controlado por PD de la Sección 15.4, Ecuación 15.4.3 con igual sensibilidad del transductor de entrada y retroalimentación,\(K_{r}=K_{\theta}\), en la forma\(\frac{\Theta(s)}{R(s)}=\frac{K_{r} P K_{a}\left(1+\tau_{d} s\right)}{J s^{2}+K_{r} P K_{a} \tau_{d} s+K_{r} P K_{a}}\). Utilice esta función de transferencia y el diagrama de bloques de la Figura 15.4.2 para escribir la ecuación algebraica para la función de transferencia del controlador PD,\(W(s) / R(s)\). Ahora, examine la naturaleza de\(W(s) / R(s)\) en los siguientes pasos:
   1. Encuentra el orden\(m\) del polinomio numerador y el orden\(n\) del polinomio denominador de\(W(s) / R(s)\). ¿Esta función de transferencia es causal o acausal, y qué significa eso en teoría respecto al realismo físico de\(W(s) / R(s)\)?
   2. Supongamos que la entrada es la función de paso infinitamente rápido\(r(t)=R_{H} H(t)\) de la tarea Problema 15.1.3. Demostrar que la transformación controlador-salida\(W(s)\) debe tener un término directo constante, como se define en la tarea Problema 2.15. ¿Cuál es el componente de respuesta temporal\(w(t)\) que corresponde al término directo de\(W(s)\), y es esta una señal físicamente realizable de un dispositivo real? Sus conclusiones de las partes 15.5.1 y 15.5.2 deben ser compatibles.
   3. Si concluyes en las partes 15.5.1 y 15.5.2 que algo es físicamente poco realista sobre estos resultados teóricos, entonces ¿qué hay en el análisis teórico que hace que los resultados sean defectuosos? Proponer un remedio que produzca resultados físicamente realizables, y mostrar sucintamente, con ecuaciones algebraicas apropiadas y explicación escrita (pero sin cálculos), por qué su remedio propuesto debería funcionar.
6. Considera el control de la actitud de tono de una nave espacial\(\theta(t)\), para lo cual la ODE del movimiento, de la Ecuación 14.2.4, es J\ ddot {\ theta} =M_ {a} (t) +M_ {d} (t), donde\(M_{d}(t)\) es un momento de perturbación. En este problema, aplicará una forma físicamente realizable de control PD, con el momento del actuador de control definido como\(M_{a}(t)=K_{a} \times w(t)\), donde\(K_{a}\) está la sensibilidad del actuador. La señal de salida del controlador PD realizable es\(*w(t)=P\left[e_{e}(t)+\tau_{d} x_{d}(t)\right]\), donde\(x_{d}(t)\) está la variable dependiente en la ODE\(\varepsilon \tau_{d} \dot{x}_{d}+x_{d}=\dot{e}_{e}\) (ver la discusión relevante en la Sección 15.4). El error de entrada es\(e_{e}(t)=K_{r} r(t)-K_{\theta} \theta(t)\), dónde\(r(t)\) está la configuración del operador de entrada,\(K_r\) y\(K_\theta\) son las sensibilidades del transductor en, respectivamente, la retroalimentación de entrada y salida.
   1. Dibuje y etiquete completamente el diagrama de bloques de Laplace de este sistema, de entrada\(R(s)\equiv L[r(t)]\) a salida\(\Theta(s) \equiv L[\theta(t)]\), incluyendo la señal de momento de perturbación\(\mathrm{M}_{\mathrm{d}}(s)=L\left[M_{d}(t)\right]\).
   2. Para\(\mathrm{M}_{\mathrm{d}}(s)=0\), derivar del diagrama de bloques de la parte 15.6.1 la función de transferencia de bucle cerrado\(\operatorname{CLTF}(s)=\Theta(s) / R(s)=\operatorname{Num}(s) / \operatorname{Den}(s)\), donde\(\operatorname{Num}(s)\) y\(\operatorname{Den}(s)\) son polinomios en potencias de\(s\). Respuesta parcial:\(\operatorname{Den}(s)=J s^{2}\left(\varepsilon \tau_{d} s+1\right)+P K_{a} K_{\theta}\left[\tau_{d}(1+\varepsilon) s+1\right]\)
   3. Para entrada paso,\(r(t)=R_{H} H(t)\), aplicar el teorema del valor final para encontrar\(\lim _{t \rightarrow \infty} \theta(t)\), siempre que el sistema sea estable.
   4. ¿\(\operatorname{CLTF}(s)\)En qué se diferencia en la parte 15.6.2, para una forma físicamente realizable de control PD, de la función de transferencia de bucle cerrado correspondiente que aplica para un controlador PD ideal pero irrealizable, para lo cual\(w(t)=P\left[e_{e}(t)+\tau_{d} \dot{e}_{d}(t)\right]\)? [No vuelva a derivar esto\(\operatorname{CLTF}(s)\) de cero; en su lugar, solo haga una simple sustitución en el\(\operatorname{CLTF}(s)\) de la parte 15.6.2.] Discutir en una o dos oraciones.
7. Consideremos el “actuador de posición” representado en el diagrama funcional Figura 15.2.2, que representa un sistema para el control de un rotor sumergido en un líquido viscoso. Supongamos que el actuador de posición es el sistema de control de la posición del rotor de la Figura 14.5.6, y que la Figura 14.5.7 es el diagrama de bloques de Laplace del actuador. Su tarea en este problema es revisar el diagrama de bloques Laplace del sistema de control de rotor sumergido, Figura 15.2.3, para incorporar la dinámica posición-actuador, reemplazando el bloque simplificado de ganancia del actuador\(K_{a}\) con una versión apropiada de la Figura 14.5.7, y haciendo necesario cualquier otro modificaciones. Se requieren al menos tres cambios significativos, siendo los dos primeros notacionales. (1) Debe volver a etiquetar la entrada de la Figura 14.5.7 modificada a\(W(s) \equiv L[w(t)]\), reemplazando\(R(s)\), y también re-etiquetar la salida a\(\Theta_{a}(s) \equiv L\left[\theta_{a}(t)\right]\), reemplazando\(\Theta(s)\). (2) Para evitar la ambigüedad notacional, debe volver a etiquetar todos los componentes del sistema en la Figura 14.5.7 que tengan símbolo subíndice\(K\)\(Q\), con símbolo subíndice, por ejemplo, en la Figura 14.5.7 revisada\(K_{r} \rightarrow Q\)\(K_{a} \rightarrow Q\), y, etc. (3) Es necesario reconocer que el resorte de rotación con rigidez\(k_{\theta}\) que se muestra en la Figura 15.2.2 impone al actuador de posición un momento\(k_{d}\left(\theta-\theta_{a}\right)\). Las cantidades etiquetadas en las Figuras 14.5.6 y 14.5.7 que pueden representar momento\(k_{d}\left(\theta-\theta_{a}\right)\) son, respectivamente,\(M_{d}(t)\) y\(\mathrm{M}_{\mathrm{d}}(s)\), por ejemplo,\(\mathrm{M}_{\mathrm{d}}(s)=k_{\theta}\left[\Theta(s)-\Theta_{a}(s)\right]\). (Sin embargo, el momento\(k_{\theta}\left(\theta-\theta_{a}\right)\) está claramente definido y no en absoluto aleatorio o impredecible matemáticamente, por lo que no es realmente una perturbación en el sentido definido en la Sección 14.2, con referencia a la Figura 14.2.1.) Contabilizando los ítems (1) - (3) y cualquier otra necesidad, dibuje un diagrama de bloques de Laplace del sistema de control de rotor sumergido, un diagrama que incorpora la dinámica posición-actuador de la Figura 14.5.7. Este diagrama de bloques será algo más largo que otros que aparecen en este libro. No se requiere que simplifique este diagrama de bloques para derivar una expresión algebraica para la función de transferencia de bucle cerrado; es posible hacerlo usando las operaciones de álgebra de diagrama de bloques descritas en los Capítulos 13 y 14, pero el proceso sería complicado algebraicamente, y sería producir una ecuación muy larga y desordenada para\(\operatorname{CLTF}(s)\). Los procesos modernos que utilizan software informático especializado son más apropiados que el álgebra a mano para una tarea como esta. Por ejemplo, si tuviera valores numéricos para todos los parámetros del sistema (\(J\)\(k_{\theta}\),\(Q_{r}\),\(\dots\),\(\tau_{1}\),\(P\),, etc.), entonces podría generar fácilmente una sola ecuación para\(\operatorname{CLTF}(s)\) con MATLAB usando las funciones tf, y retroalimentación y series (o, en lugar de series, simplemente la operación de multiplicación de la función de transferencia).