16.2: Sistemas de rotor controlado por PD estable y Snstable

En esta sección, analizamos en detalle un ejemplo específico de la teoría desarrollada en la Sección 16.1. La situación considerada es ideal control proporcional-derivado (PD) de posición\(\theta(t)\) de un rotor con inercia significativa\(J\), como se describe en la Sección 15.4 y tarea Problema 15.1. La sensibilidad de los transductores idénticos de entrada y salida-retroalimentación se denota\(K_{r}=K_{\theta}\), la sensibilidad del actuador de momento es\(K_{a}\), y, para el controlador PD ideal, la ganancia proporcional es\(P\) y la constante de tiempo derivada es\(\tau_{d}\). La función de transferencia de este sistema, de las Ecuaciones 15.4.3 y 15.4.4, es

\[\frac{\Theta(s)}{R(s)}=\frac{\omega_{n}^{2}\left(\tau_{d} s+1\right)}{s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}}\label{eqn:16.14} \]

con 2 ^parámetros estándar del sistema de pedido definidos como

\[\omega_{n}=\sqrt{\frac{K_{r} K_{a} P}{J}} \text { and } \zeta=\frac{1}{2} \omega_{n} \tau_{d}\label{eqn:15.28} \]

Lo primero que podemos hacer con la función de transferencia Ecuación\(\ref{eqn:16.14}\) es inferir la ecuación diferencial ordinaria del sistema (ODE) mediante la transformación inversa de Laplace:

\[\left[s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}\right] \Theta(s)=\left[\omega_{n}^{2}\left(\tau_{d} s+1\right)\right] R(s) \Rightarrow \ddot{\theta}+2 \zeta \omega_{n} \dot{\theta}+\omega_{n}^{2} \theta=\omega_{n}^{2}\left(\tau_{d} \dot{r}+r\right)\label{eqn:16.15} \]

Recordemos que la función de transferencia se basa en cero ICs para la salida. Pero ahora queremos dar cuenta de los CI, así que tomemos la transformación completa de Laplace de la ODE, incluyendo los CI posiblemente distintos de cero, la tasa de rotación inicial\(\dot{\theta}(0) \equiv \dot{\theta}_{0}\) y la posición inicial\(\theta(0) \equiv \theta_{0}\):

\[\left[s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}\right] \Theta(s)-s \theta_{0}-\dot{\theta}_{0}-2 \zeta \omega_{n} \theta_{0}=\left[\omega_{n}^{2}\left(\tau_{d} s+1\right)\right] R(s)\label{eqn:16.16} \]

La solución de la ecuación\(\ref{eqn:16.16}\) para la transformación de salida es

\[\Theta(s)=\frac{\theta_{0} s+\left(\dot{\theta}_{0}+2 \zeta \omega_{n} \theta_{0}\right)}{s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}}+\frac{\omega_{n}^{2}\left(\tau_{d} s+1\right)}{s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}} R(s)\label{eqn:16.17} \]

Comparar solución de transformación específica Ecuación\(\ref{eqn:16.17}\) con la forma general Ecuación 16.1.5. A continuación, factoricemos el polinomio denominador de la función de transferencia. Es conveniente para ello asumir eso\(|\zeta|<1\), y definir la frecuencia natural positiva, real, amortiguada como\(\omega_{d}=\omega_{n} \sqrt{1-\zeta^{2}}\). Puede derivar fácilmente de la fórmula cuadrática (o simplemente sustituir en el lado derecho para verificar) la factorización:

\[s^{2}+2 \zeta \omega_{n} s+\omega_{n}^{2}=(s-p)(s-\bar{p}), \text { where the complex pole is } p=-\zeta \omega_{n}+j \omega_{d}\label{eqn:16.18} \]

Por lo tanto, reescribimos la ecuación de transformación\(\ref{eqn:16.17}\), y la expresamos en términos de componentes de respuesta IC y respuesta forzada:

\[\Theta(s)=\frac{\theta_{0} s+\left(\dot{\theta}_{0}+2 \zeta \omega_{n} \theta_{0}\right)}{(s-p)(s-\bar{p})}+\frac{\omega_{n}^{2}\left(\tau_{d} s+1\right)}{(s-p)(s-\bar{p})} R(s) \equiv \Theta_{i c}(s)+\Theta_{f}(s)\label{eqn:16.19} \]

El término de respuesta IC de la ecuación\(\ref{eqn:16.19}\) se expande en forma de fracción parcial:

\[\Theta_{i c}(s) \equiv \frac{\theta_{0} s+\left(\dot{\theta}_{0}+2 \zeta \omega_{n} \theta_{0}\right)}{(s-p)(s-\bar{p})}=\frac{C}{(s-p)}+\frac{\bar{C}}{(s-\bar{p})}\label{eqn:16.20} \]

Usando el método convencional de ahorro de mano de obra parcial-fracción-expansión de las Secciones 2.2 y 2.3, y\(p=-\zeta \omega_{n}+j \omega_{d}\) de la Ecuación\(\ref{eqn:16.18}\), y un poco de álgebra, encontramos el siguiente residuo complejo de la Ecuación\(\ref{eqn:16.20}\):

\[C=\left[(s-p) \Theta_{i c}(s)\right]_{s=p}=\left[\frac{\theta_{0} p+\left(\dot{\theta}_{0}+2 \zeta \omega_{n} \theta_{0}\right)}{(s-\bar{p})}\right]_{s=p}=\frac{1}{2}\left(\theta_{0}-j \frac{\dot{\theta}_{0}+\zeta \omega_{n} \theta_{0}}{\omega_{d}}\right)\label{eqn:16.21} \]

Por lo tanto, la sustitución de Ecuaciones\(\ref{eqn:16.18}\) y\(\ref{eqn:16.20}\) en la ecuación de transformación inversa 16.1.12 da la respuesta IC [con\(C\) dada por la ecuación\(\ref{eqn:16.21}\)]:

\[\theta_{i c}(t)=L^{-1}\left[\Theta_{i c}(s)\right]=2|C| e^{-\zeta \omega_{n} t} \cos \left(\omega_{d} t+\angle C\right)\label{eqn:16.22} \]

A continuación, derivemos la respuesta forzada de este sistema controlado a una entrada específica, no trivial, el pulso exponencial en rampa\(r(t)=R_{p}(t / \tau) e^{-t / \tau}\), cuyo valor máximo es\(r_{\max }=r(t=\tau)=R_{p} e^{-1}\). La transformada de Laplace de este pulso es\(R(s)=\left(R_{p} / \tau\right) /(s+1 / \tau)^{2}\). La transformación de la respuesta forzada, de Ecuación\(\ref{eqn:16.19}\), es

\[L\left[\theta_{f}(t)\right]=\frac{\omega_{n}^{2}\left(\tau_{d} s+1\right)}{(s-p)(s-\bar{p})} R(s)=\frac{\omega_{n}^{2}\left(\tau_{d} s+1\right)}{(s-p)(s-\bar{p})} \frac{R_{p} / \tau}{(s+1 / \tau)^{2}}=R_{p} \frac{\omega_{n}^{2}}{\tau} \frac{\tau_{d} s+1}{(s-p)(s-\bar{p})(s+1 / \tau)^{2}}\label{eqn:16.23} \]

La fracción de polinomios en Ecuación se\(\ref{eqn:16.23}\) puede expandir en la siguiente forma:

\[L\left[\theta_{f}(t)\right] / R_{p} \frac{\omega_{n}^{2}}{\tau} \equiv F_{f}(s)=\frac{\tau_{d} s+1}{(s-p)(s-\bar{p})(s+1 / \tau)^{2}}=\frac{C R}{s-p}+\frac{\overline{C R}}{s-\bar{p}}+\frac{A}{(s+1 / \tau)^{2}}+\frac{B}{s+1 / \tau}\label{eqn:16.24} \]

\(CR\)\(A\),, y\(B\) son constantes que necesitamos encontrar. No nos hemos encontrado previamente con un caso de polos repetidos como este. Los dos últimos términos del lado derecho en Ecuación\(\ref{eqn:16.24}\) muestran la forma que debe tener una expansión de fracción parcial para polos repetidos (Ogata, 1998, p. 33). Encontramos residuos complejos\(CR\) utilizando el método convencional:

\[C R=\left[(s-p) F_{f}(s)\right]_{s=p}=\frac{\tau_{d} p+1}{(p-\bar{p})(p+1 / \tau)^{2}}=\frac{\tau_{d} p+1}{j 2 \omega_{d}(p+1 / \tau)^{2}}\label{eqn:16.25} \]

en el que\(p=-\zeta \omega_{n}+j \omega_{d}\). Para encontrar constantes\(A\) y\(B\), es útil multiplicar a través de Ecuación\(\ref{eqn:16.24}\) por el factor denominador con polos repetidos (Ogata, 1998, p. 33):

\[(s+1 / \tau)^{2} F_{f}(s)=\frac{\tau_{d} s+1}{(s-p)(s-\bar{p})}=(s+1 / \tau)^{2}\left(\frac{C R}{s-p}+\frac{\overline{C R}}{s-\bar{p}}\right)+A+(s+1 / \tau) B\label{eqn:16.26} \]

A partir de Ecuación\(\ref{eqn:16.26}\), encontramos fácilmente constante\(A\) usando el método convencional:

\[A=\left[(s+1 / \tau)^{2} F_{f}(s)\right]_{s=-1 / \tau}=\frac{-\tau_{d} / \tau+1}{(-1 / \tau-p)(-1 / \tau-\bar{p})}=\frac{1-\tau_{d} / \tau}{(1 / \tau+p)(1 / \tau+\bar{p})}\label{eqn:16.27} \]

Encontrar constante\(B\) se agiliza diferenciando primero la ecuación\(\ref{eqn:16.26}\) con respecto a\(s\), de modo que esa constante\(B\) se mantiene sola en el último término del lado derecho:

\[\frac{d}{d s}\left[(s+1 / \tau)^{2} F_{f}(s)\right]=\frac{(s-p)(s-\bar{p}) \tau_{d}-\left(\tau_{d} s+1\right)(2 s-p-\bar{p})}{[(s-p)(s-\bar{p})]^{2}} \nonumber \]

\[=\frac{d}{d s}\left[(s+1 / \tau)^{2}\left(\frac{C R}{s-p}+\frac{\overline{C R}}{s-\bar{p}}\right)\right]+B\label{eqn:16.28} \]

\[=2(s+1 / \tau)\left(\frac{C R}{s-p}+\frac{\overline{C R}}{s-\bar{p}}\right)+(s+1 / \tau)^{2} \frac{d}{d s}\left(\frac{C R}{s-p}+\frac{\overline{C R}}{s-\bar{p}}\right)+B \nonumber \]

Por lo tanto, encontramos constante\(B\) evaluando Ecuación\(\ref{eqn:16.28}\) en\(s=-1 / \tau\):

\[B=\left\{\frac{(s-p)(s-\bar{p}) \tau_{d}-\left(\tau_{d} s+1\right)(2 s-p-\bar{p})}{[(s-p)(s-\bar{p})]^{2}}\right\}_{s=-1 / z} \nonumber \]

\[=\frac{(1 / \tau+p)(1 / \tau+\bar{p}) \tau_{d}+\left(1-\tau_{d} / \tau\right)(2 / \tau+p+\bar{p})}{[(1 / \tau+p)(1 / \tau+\bar{p})]^{2}}\label{eqn:16.29} \]

A pesar de\(p\) que es complejo\(p=-\zeta \omega_{n}+j \omega_{d}\), las constantes\(A\) en Ecuación\(\ref{eqn:16.27}\) y\(B\) en Ecuación\(\ref{eqn:16.29}\) resultan ser reales. Los factores que parecen ser complejos son:\((1 / \tau+p)(1 / \tau+\bar{p})=\left(1 / \tau-\zeta \omega_{n}+j \omega_{d}\right)\left(1 / \tau-\zeta \omega_{n}-j \omega_{d}\right)=\left(1 / \tau-\zeta \omega_{n}\right)^{2}+\omega_{d}^{2}\), que es real; y\(2 / \tau+p+\bar{p}=2\left(1 / \tau-\zeta \omega_{n}\right)\), que también es real. Así, las fórmulas finales, más claramente reales para las constantes\(A\) en Ecuación\(\ref{eqn:16.27}\) y\(B\) en Ecuación\(\ref{eqn:16.29}\) son

\[A=\frac{1-\tau_{d} / \tau}{\left(1 / \tau-\zeta \omega_{n}\right)^{2}+\omega_{d}^{2}}, B=\frac{\left[\left(1 / \tau-\zeta \omega_{n}\right)^{2}+\omega_{d}^{2}\right] \tau_{d}+2\left(1-\tau_{d} / \tau\right)\left(1 / \tau-\zeta \omega_{n}\right)}{\left[\left(1 / \tau-\zeta \omega_{n}\right)^{2}+\omega_{d}^{2}\right]^{2}}\label{eqn:16.30} \]

Con residuo complejo\(CR\) de Ecuación\(\ref{eqn:16.25}\), y constantes reales\(A\) y\(B\) de Ecuación\(\ref{eqn:16.30}\), la ecuación de respuesta forzada se encuentra a partir de la transformada inversa de la Ecuación\(\ref{eqn:16.24}\):

\[\theta_{f}(t)=R_{p} \frac{\omega_{n}^{2}}{\tau} L^{-1}\left[F_{f}(s)\right]=R_{p} \frac{\omega_{n}^{2}}{\tau}\left[2|C R| e^{-\zeta \omega_{n} t} \cos \left(\omega_{d} t+\angle C R\right)+(A t+B) e^{-t / \tau}\right]\label{eqn:16.31} \]

Los términos\((A t+B) e^{-t / \tau}\) en Ecuación\(\ref{eqn:16.31}\) están asociados con los polos de la función de forzamiento\(r(t)=R_{p}(t / \tau) e^{-t / \tau}\). Observe que estos términos varían en el tiempo de manera similar a\(r(t)\), pero que no tienen influencia sobre la estabilidad positiva o negativa del sistema. Sólo la función exponencial\(e^{-\zeta \omega_{n} t}\), que está en el término asociada con los polos del sistema (función de transferencia), determina el estado de estabilidad del sistema.

La ecuación de salida completa es la combinación de Ecuación de respuesta IC\(\ref{eqn:16.22}\) y Ecuación de respuesta forzada\(\ref{eqn:16.31}\):

\[\theta(t)=\theta_{i c}(t)+\theta_{f}(t)\label{eqn:16.32} \]

Calculemos y trazemos las respuestas para un sistema en particular. Los parámetros básicos son: inercia del rotor\(J=0.00256\) lb-s ² -inch (la inercia de una pequeña rueda de aluminio de aproximadamente cuatro pulgadas de diámetro); y producto de sensibilidades\(K_{r} K_{a}=0.0350\) lb-pulgadas/radián. Especificemos para el sistema de bucle cerrado: frecuencia natural no amortiguada\(f_{n}=\omega_{n} /(2 \pi)=1.0\) Hz (para que el tiempo de aumento de respuesta escalonada sea de alrededor de ¼ s); y relaciones de amortiguación\(\zeta=+0.12\) para un caso de estabilidad positiva, y\(\zeta=-0.03\) para un caso de inestabilidad. El archivo MATLAB a continuación utiliza la Ecuación 15.4.4 para calcular la ganancia proporcional\(P=\omega_{n}^{2} J /\left(K_{r} K_{a}\right)=2.888\) y las constantes de tiempo derivadas\(\tau_{d}=2 \zeta / \omega_{n}=0.0382\) s y −0.00955 s enumeradas en la salida alfanumérica para los dos casos diferentes.

Para tener condiciones iniciales no triviales, especifiquemos la velocidad de rotación inicial\(\dot{\theta}(0) \equiv \dot{\theta}_{0}=-0.29\) rad/s y el\(\theta(0) \equiv \theta_{0}=-0.025\) radián de posición inicial. Para la función de entrada ramped-exponencial\(r(t)=R_{p}(t / \tau) e^{-t / \tau}\), especifiquemos magnitud\(R_{p}=0.1 \times e\) radián = 0.2718 radianes y constante de tiempo\(\tau=1.5\) s, de manera que\(r_{\max }=R_{p} e^{-1}=0.1\) radian en el tiempo\(t=1.5\) s. (La mayoría de los valores de entrada especificados anteriormente fueron elegidos por ensayo y error para producir gráficos claros e instructivos salida.)

A continuación se muestra un archivo M de script MATLAB para calcular y graficar la respuesta:

%Matlabdemo161.m

% de estabilidad de un rotor controlado por PD

%Excitación con condiciones iniciales y pulso exponencial en rampa

J=2.56e-3; Krka=0.035; fn=1; wn=2*pi*fn; p=Wn^2*J/KRKa;

disp ('P ='), disp (P)

zeta= [0.12 -0.03];

para nc= 1:2;

zt=zeta (nc); wd=wn*sqrt (1-zt^2); p=-zt*wn+j*wd; td=2*zt/WN;

disp ('Caso #, zeta, Td, p ='), disp ([nc zt Td p])

%respuesta de condición inicial

th0=-0.025; dth0=-0.29;

C =( th0-j* (dth0+zt*wn*th0) /wd) /2; ABC=ABS (C); ANC=Ángulo (C);

t=0:. 05:10;

Thic=2*ABC*exp (-zt*wn*t). *cos (wd*t+ANC);

%Respuesta forzada

Rp=0.1*exp (1); tau=1.5; R=RP/tau*t.*exp (-t/tau);

CR= (TD*p+1)/(j*2*wd* (p+1/tau) ^2); ABCR=ABS (CR); ANCR=Ángulo (CR);

C1=1-TD/tau; c2=1/tau-zt*wn; c3=c2^2+wd^2; a=C1/c3;

B =( C3*td+2* (1-tD/tau) *c2) /c3^2;

THF=RP*Wn^2/tau* (2*ABCR*exp (-zt*wn*t). *cos (Wd*t+ANCR) + (A*t+b). *exp (-t/tau));

subparcela (2,1, nc), parcela (t, thic+THF, t, r), rejilla

final

El comando para ejecutar el archivo M, y la salida alfanumérica resultante y la salida gráfica (después del uso de las características de edición de MATLAB para anotación y mejora gráfica) son:

>> MatlabDemo161

P =

2.8876

Caso #, zeta, Td, p =

1.0000 0.1200 0.0382 -0.7540 + 6.2378i

Caso #, zeta, Td, p =

2.0000 -0.0300 -0.0095 0.1885 + 6.2804i

Figura\(\PageIndex{1}\): Ajuste del operador de entrada exponencial Ramped-Exponencial\(r(t)\) y posiciones del rotor de salida\(\theta(t)\) para un rotor controlado por derivativo proporcional (PD) ideal, con dos constantes de tiempo derivadas diferentes. (Copyright; autor vía fuente)

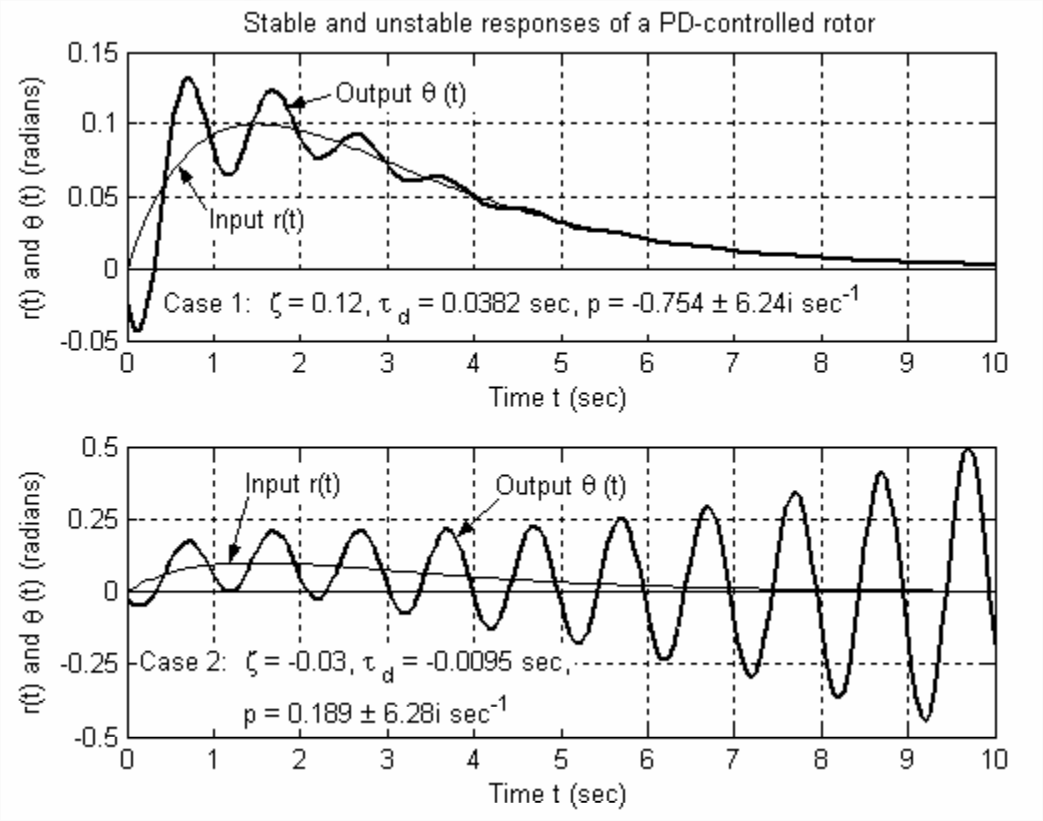
El caso 1 de la Figura\(\PageIndex{1}\) muestra un buen desempeño del sistema de control PD: a pesar de condiciones iniciales bastante adversas, la salida sigue muy bien la entrada, especialmente después de que la respuesta transitoria inicial ha decaído. En la práctica normal de la ingeniería, la constante de tiempo derivada probablemente se\(\tau_{d}\) establecería considerablemente más alta que en este caso académico, lo que suprimiría la oscilación transitoria aún más rápidamente y produciría una respuesta aún mejor controlada.

El caso 2, en cambio, exhibe una grave inestabilidad dinámica, lo que sería inaceptable en la práctica normal de ingeniería. Tenga en cuenta las diferentes escalas de\(y\) eje para los Casos 1 y 2. En la vida real, las oscilaciones continuarían creciendo exponencialmente hasta que alguna parte mecánica o eléctrica fallara (posiblemente un fusible protector diseñado para fallar bajo una carga excesiva), o algún gobernador mecánico limitaría el movimiento, o algún componente eléctrico (por ejemplo, un amplificador operacional) saturar, o hasta que el sistema de control de alguna manera se desactivara intencionalmente. Este ejemplo demuestra que los sistemas de control de retroalimentación pueden ser peligrosos; los ingenieros deben diseñar y probar cualquier sistema de control de retroalimentación con mucho cuidado para garantizar que sea positivamente estable y seguro.