16.6: Funciones de Transferencia de Bucle Abierto y Loci de Raíces

Revisemos y consideremos nuevamente la Figura 14.4.1, el diagrama de bloques general de Laplace para un sistema de bucle cerrado SISO con retroalimentación. En la Sección 14.4, se utilizó la Figura 14.4.1 para derivar la función de transferencia de bucle cerrado\(\operatorname{Out}(s) / \operatorname{In}(s)\):

\[C L T F(s)=\frac{G}{1+G H}=\frac{N_{G} D_{H}}{D_{G} D_{H}+N_{G} N_{H}}\label{eqn:16.60} \]

Figura\(\PageIndex{1}\): Diagrama de bloques de Laplace de bucle cerrado general. (Copyright; autor vía fuente)

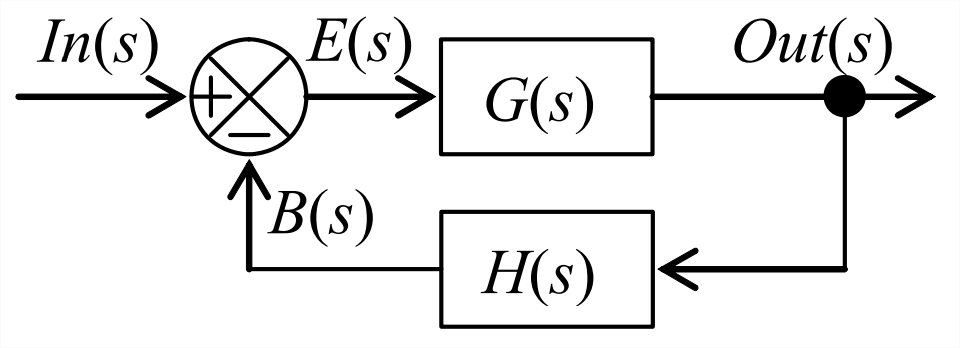
También es práctica común referirse a la relación\(B(s) / E(s)\) como la función de transferencia de bucle abierto, que se expresa más completamente como

\[\frac{B(s)}{E(s)} \equiv O L T F(s)=G(s) H(s)=\frac{N_{G}(s) N_{H}(s)}{D_{G}(s) D_{H}(s)} \equiv C \times \frac{\prod_{k=1}^{m}\left(s-Z_{k}\right)}{\prod_{k=1}^{n}\left(s-P_{k}\right)}\label{eqn:16.61} \]

En Ecuación\(\ref{eqn:16.61}\),\(C\) hay alguna constante física, los ceros finitos\(Z_{k}\) de\(\operatorname{OLTF}(s)\) son las raíces de\(N_{G}(s) N_{H}(s)=0\), y los polos\(P_{k}\) de\(\operatorname{OLTF}(s)\) son las raíces de\(D_{G}(s) D_{H}(s)=0\). [Porque\(n>m\), también hay\(n-m\) ceros de\(\operatorname{OLTF}(s)\) as\(s \rightarrow \infty\).]

El polinomio característico de grado\(n\) ^th del sistema de bucle cerrado es la Ecuación 16.5.16,\(a_{1} \prod_{k=1}^{n}\left(p-p_{k}\right)=0\). Tenga en cuenta que el denominador de\(\operatorname{CLTF}(s)\), Ecuación\(\ref{eqn:16.60}\), es igual al denominador más el numerador de\(\operatorname{OLTF}(s)\), Ecuación\(\ref{eqn:16.61}\). Por lo tanto, después de dividir el coeficiente\(a_{1}\), la ecuación característica para los polos del sistema de bucle cerrado generalmente se\(p\) puede poner en una de las siguientes formas:

\ [D_ {G} (p) D_ {H} (p) +N_ {G} (p) N_ {H} (p) =0\ Rightarrow\ left\ {\ begin {array} {l}
\ text {(a)}\ prod_ {k=1} ^ {n}\ left (p-p_ {k}\ right) +c\ lambda=0\
\ texto {(b)}\ prod_ {k=1} ^ {n}\ izquierda (p-p_ {k}\ derecha) +c\ lambda\ prod_ {k=1} ^ {m}\ left (p-z_ {k}\ right) =0
\ end {array}\ right. \ label {eqn:16.62}\]

En Ecuaciones\(\ref{eqn:16.62}\),\(c\) se conoce alguna constante física, y\(\Lambda\) es el parámetro de control variable. El sistema evaluado por métodos de locus raíz en la Sección 16.5 incluye polos de bucle abierto\(P_k\) (llamados allí los “polos del subsistema”), pero no ceros finitos de bucle abierto\(Z_k\), de manera que la ecuación característica del sistema, la Ecuación 16.5.2, es de forma Ecuación\(\ref{eqn:16.62}\) .a. Por otro lado, los sistemas de tarea Los problemas 16.8, 16.9 y 16.10 tienen tanto polos de bucle abierto como ceros de bucle abierto, por lo que sus ecuaciones características tienen forma Ecuación\(\ref{eqn:16.62}\) .b.

Algunas características simples pero generales de los loci de raíces de bucle cerrado se pueden inferir a partir de las ecuaciones\(\ref{eqn:16.62}\). Ambas ecuaciones muestran claramente que cuando\(\Lambda=0\), los polos de bucle cerrado son exactamente los mismos que los polos de bucle abierto. En el otro extremo, como\(\Lambda\) se vuelve muy grande\(\Lambda \rightarrow \infty\),,\(m\) de los loci\(\rightarrow\) los ceros finitos de bucle abierto\(Z_{k}\). Esto es obvio a partir de la Ecuación\(\ref{eqn:16.62}\) .b, porque el término que incluye los polos de bucle abierto se vuelve progresivamente menos significativo en tamaño relativo a medida que\(\Lambda\) aumenta la magnitud de los polos.

Al igual que\(\Lambda \rightarrow \infty\) en la Ecuación\(\ref{eqn:16.62}\) .a, para que una ecuación de igualdad de magnitud como la Ecuación 16.5.7\(r_{1} r_{2} r_{3}=\omega_{b} \Lambda\),, permanezca satisfecha, todos los\(n\) loci de esa ecuación deben ir a algunas\(\infty\) ubicaciones en el\(p\) plano. De manera similar, como\(\Lambda \rightarrow \infty\) en la Ecuación\(\ref{eqn:16.62}\) .b, aunque\(m\) de los loci terminan en los ceros finitos de bucle abierto\(Z_k\), los\(n-m\) loci restantes deben ir a algunas\(\infty\) ubicaciones en el\(p\) plano. Para ambas Ecuaciones\(\ref{eqn:16.62}\) como\(\Lambda \rightarrow \infty\), los valores de los ceros finitos de bucle abierto\(Z_k\) y de los polos de bucle abierto\(P_k\) tienen una influencia secundaria, por lo que las direcciones\(\theta_{A}\) en el\(p\) plano -de las asíntotas de\(n - m\) línea recta de los\(\Lambda \rightarrow \infty\) loci son las soluciones para ángulos de\(p^{n-m}+c \Lambda=0\), lo que lleva a:

\[\left(r e^{j \theta_{A}}\right)^{n-m}=c \Lambda \exp [j(\pm \pi, \pm 3 \pi, \ldots)] \Rightarrow(n-m) \theta_{A}=\pm \pi, \pm 3 \pi, \ldots \nonumber \]

\[\theta_{A}=\frac{1}{n-m}(\pm \pi, \pm 3 \pi, \ldots)\label{eqn:16.63} \]

Sin embargo, Ecuación\(\ref{eqn:16.63}\) descuida los valores de\(Z_k\) y\(P_k\), por lo que implica incorrectamente que las asíntotas “irradian” (o “emanan”) desde el origen del\(p\) plano; de hecho, se puede probar (Cannon, 1967, páginas 658-659) que todas las\(n - m\) asíntotas emanan de un punto en el eje real definido por la ecuación:

\[p_{A}=\frac{1}{n-m}\left(\sum_{k=1}^{n} \operatorname{Re}\left[P_{k}\right]-\sum_{k=1}^{m} \operatorname{Re}\left[Z_{k}\right]\right)\label{eqn:16.64} \]

También es útil conocer las direcciones en las que los loci “parten” de los polos de bucle abierto a medida que\(\Lambda\) aumenta desde cero. Supongamos que buscamos la dirección (ángulo) de salida\(\left(\theta_{j}\right)_{d e p}\) del locus de raíces de bucle cerrado desde el polo de bucle abierto\(P_{j}\). Usemos la siguiente notación:\((\theta P)_{k j}\) es el ángulo de polo de bucle abierto\(P_{k}\) a polo de bucle abierto\(P_{j}\); y\((\theta Z)_{k j}\) es el ángulo de cero de bucle abierto\(Z_k\) a polo de bucle abierto\(P_{j}\). Siempre que todos los polos y ceros de bucle abierto sean raíces simples (no repetidas o múltiples), entonces se calcula el ángulo requerido a partir de la ecuación (Cannon, 1967, páginas 660-661):

\[\left(\theta_{j}\right)_{d e p}=\pi-\sum_{k=1 \atop k \neq j}^{n}(\theta P)_{k j}+\sum_{k=1}^{m}(\theta Z)_{k j}\label{eqn:16.65} \]

Utilizamos el ejemplo numérico de la Sección 16.5 para ilustrar la información sobre loci de raíces que es proporcionada por polos de bucle abierto; ese ejemplo es un sistema de ^tercer orden para el cual\(n=3\) y\(m=0\). De la Ecuación 16.5.2 con\(\Lambda=0\), los polos de bucle abierto son\(p_{1}=0\)\(p_{2}=-100\) s ^-1, s ^-1 y\(p_{3}=-300\) s ^-1. Estos polos de bucle abierto están marcados por\(\times\)'s en la Figura\(\PageIndex{2}\). No hay ceros de bucle abierto, por lo que\(\Lambda \rightarrow \infty\), los tres loci deben ir a algunas\(\infty\) ubicaciones en el\(p\) plano -; las direcciones de las líneas asintóticas a estos loci están dadas por la Ecuación\(\ref{eqn:16.63}\) as\(\theta_{A}=\pm \pi / 3\) y\(\theta=\pi\). El punto en el eje real del que emanan las tres asíntotas viene dado por la Ecuación\(\ref{eqn:16.64}\) como\(p_{A}=(0-100-300) / 3=-133\frac{1}{3}\) s ^-1. Las asíntotas son las líneas discontinuas rectas en la Figura\(\PageIndex{2}\). La ecuación\(\ref{eqn:16.65}\) da los ángulos de salida de los polos de bucle abierto como\(\left(\theta_{1}\right)_{d e p}=\pi-(0+0)=\pi\),\(\left(\theta_{2}\right)_{d e p}=\pi-(\pi+0)=0\), y\(\left(\theta_{3}\right)_{d e p}=\pi-(\pi +\pi)=-\pi\). Estos ángulos de partida se representan en la Figura\(\PageIndex{2}\) mediante flechas cortas y negrita. Si bien las direcciones de partida para este sistema en particular son debidas al este o al oeste, no siempre es así; para los sistemas en general, una dirección de salida puede ser cualquier ángulo.

Figura\(\PageIndex{2}\): Ejemplo de información sobre loci de raíces que es proporcionada por los polos de bucle abierto. (Copyright; autor vía fuente)

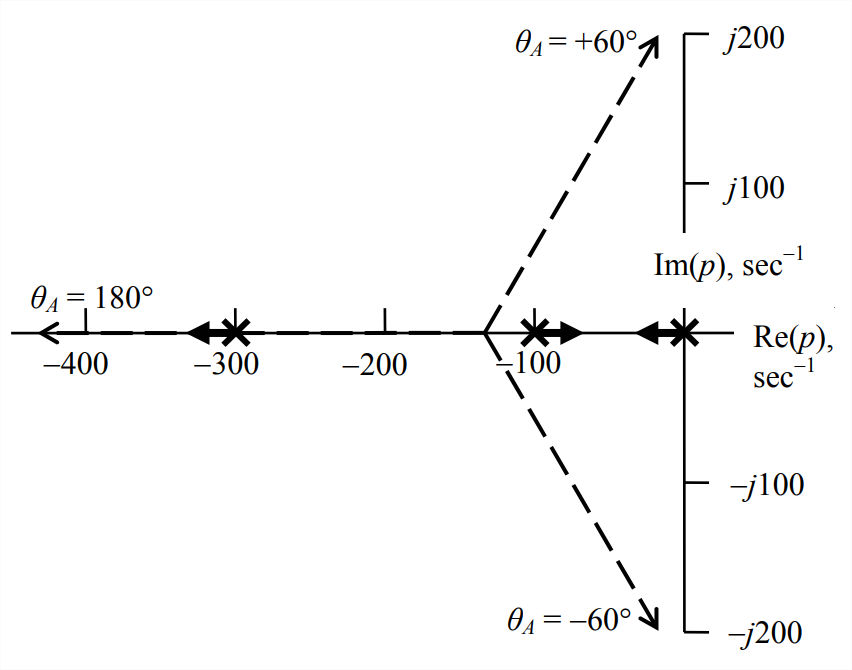
Podemos hacer conjeturas educadas en cuanto a la aparición del diagrama completado de loci raíz, incluso a partir del diagrama incompleto Figura\(\PageIndex{2}\). Primero, parece probable que el locus que se origina (es decir, for\(\Lambda=0\)) en el polo de bucle abierto\(p_{3}=-300\) s ^-1 simplemente proceda hacia el oeste a lo largo de la asíntota\(\theta_{A}=\pi\), sin alejarse del\(\operatorname{Re}(p)\) eje. Siendo ese el caso, entonces los loci que se originan en los polos de bucle abierto\(p_{1}=0\)\(p_{2}=-100\) s ^{-1 y s -1} deben acercarse inicialmente entre sí, luego reunirse en algún lugar entre\(p_{1}\) y\(p_{2}\), y luego separarse del\(\operatorname{Re}(p)\) eje y convertirse en el complejo par conjugado de curvas a las que las asíntotas\(\theta_{A}=\pm \pi / 3\) son tangentes como\(\Lambda \rightarrow \infty\). Ciertamente, el diagrama incompleto Figura\(\PageIndex{2}\) es cualitativamente similar al diagrama exacto Figura 16.5.5, e\(\PageIndex{2}\) incluso la Figura incluye parte de la misma información cuantitativa significativa.

Cuando utilice software para determinar loci de raíces, también debe hacer los cálculos fáciles presentados en esta sección basados en polos y ceros de bucle abierto. Si los cálculos del software coinciden con los suyos, entonces esta comprobación validará (parcialmente, al menos) que el software es correcto y que lo está utilizando correctamente.