17.2: Parcelas Nyquist

Última actualización
Guardar como PDF

Page ID: 84681

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Ahora nos apartamos temporalmente del análisis de estabilidad para describir un tipo de representación gráfica de frecuencia-respuesta que no ha aparecido previamente en este libro. A tal gráfica se le suele llamar, en el lenguaje de la ingeniería de sistemas de control, diagrama o trama Nyquist.

Comenzamos la descripción de las parcelas Nyquist volviendo a visitar un sistema familiar de varios capítulos anteriores: el sistema estándar, amortiguado positivamente ^{de segundo} orden. La ODE de este sistema para la salida\(x(t)\) en respuesta a la entrada\(u(t)\) es\(\ddot{x}+2 \zeta \omega_{n} \dot{x}+\omega_{n}^{2} x=\omega_{n}^{2} u(t)\) [Ecuación 9.2.2], y la función de frecuencia-respuesta es

\[F R F(\omega)=\frac{\omega_{n}^{2}}{\omega_{n}^{2}-\omega^{2}+j 2 \zeta \omega_{n} \omega}\label{eqn:10.7} \]

La representación gráfica anterior de la Ecuación\(\ref{eqn:10.7}\) en este libro es la Figura 10.2.1, un diagrama Bode modificado que muestra la variación con frecuencia\(\omega\) de los componentes polares, relación de magnitud\(|F R F(\omega)|\) y ángulo de fase\(\phi=\angle F R F(\omega)\). Una gráfica Nyquist, en contraste, muestra directamente los componentes matemáticos rectangulares, en el formato\(\operatorname{Im}[F R F(\omega)]\) versus\(\operatorname{Re}[F R F(\omega)]\),\(\omega\) siendo la frecuencia la variable independiente implícita, para la cual no hay escala graduada sin anotación extra o un tercer eje tridimensional perpendicular al\(F R F(\omega)\) plano complejo. Por ejemplo, los siguientes comandos de MATLAB producen Figura\(\PageIndex{1}\), una gráfica Nyquist de Ecuación\(\ref{eqn:10.7}\) para\(\omega_{n} = 2\pi\) rad/s de frecuencia natural no amortiguada y relación de amortiguación\(\zeta=0.2\):

>> wn=2*pi; zt=0.2;

>> w=wn*logspace (-2,2,400);

>> frf=wn^2. /(wn^2-w.^2+j*2*zt*wn*w);

>> parcela (real (frf), imag (frf)), cuadrícula

Figura\(\PageIndex{1}\): Gráfica nyquist de\(F R F(\omega)=\omega_{n}^{2} /\left(\omega_{n}^{2}-\omega^{2}+j 2 \zeta \omega_{n} \omega\right)\) para\(\omega_{n}=2 \pi\) rad/s y\(\zeta=0.2\). (Copyright; autor vía fuente)

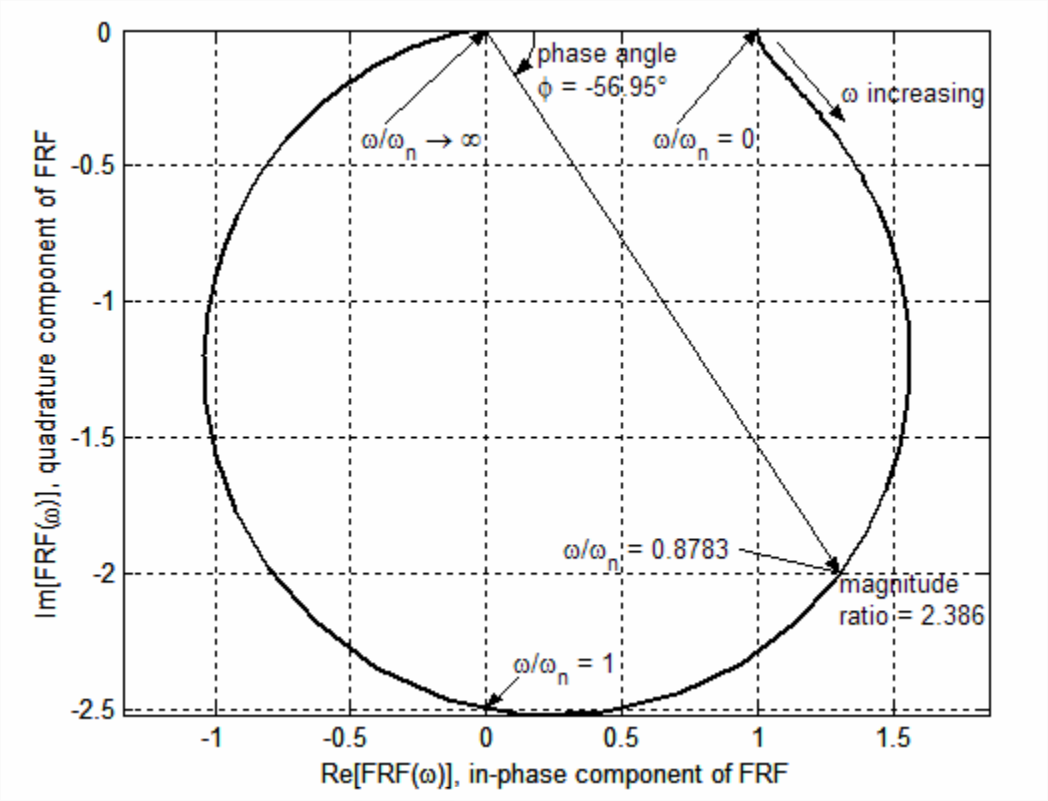
Observe en la Figura\(\PageIndex{1}\) que los ejes de abscisas y ordenadas están etiquetados tanto con las descripciones matemáticas,\(\operatorname{Re}[F R F(\omega)]\) como de la siguiente manera: primero, medir los componentes polares de respuesta, relación de magnitud\(|F R F(\omega)|\) y ángulo de fase\(\phi(\omega)=\angle F R F(\omega)\), utilizando el procedimiento descrito en\(\operatorname{Im}[F R F(\omega)]), and with the corresponding physical descriptions of the response components, respectively: in-phase (0°, also known as coincident) and quadrature (leading by 90°). If you were measuring frequency response experimentally on a damped 2^nd order system you might generate the physical information of Figure \(\PageIndex{1}\) Sección 17.1 relativa a la Figura 17.1.3, el diagrama Bode modificado; luego, use la Ecuación 2.1.7 para convertir números complejos de forma polar a forma rectangular para calcular\(F R F_{\text {in-phase}}(\omega)=|F R F(\omega)| \times \cos \phi(\omega)\) y\(F R F_{\text {quadrature}}(\omega)=|F R F(\omega)| \times \sin \phi(\omega)\). Un ejemplo de esta conversión se ilustra en la Figura\(\PageIndex{1}\) para\(\omega=0.8783 \omega_{n}\):\(1.301 = 2.386 \times \cos \left(-56.95^{\circ}\right)\), y\(-2.000=2.386 \times \sin \left(-56.95^{\circ}\right)\).

El concepto de componentes físicos en fase y cuadratura de frecuencia-respuesta puede parecer extraño. Además, sus valores pueden ser positivos o negativos (como\(\PageIndex{1}\) muestra la Figura para el componente en fase), y eso podría ser confuso: si una respuesta pura “en fase” es negativa, entonces la respuesta es realmente 180° desfasada con la excitación; y si una respuesta pura de “cuadratura” es negativo, entonces la respuesta en realidad retarda la excitación 90°. Para brindar mayor claridad, incluso a riesgo de ser redundante, presentamos la siguiente tabla, que enumera valores múltiples de 90° de ángulo de fase\(\phi\) que corresponden a valores o rangos particulares de los componentes en fase y cuadratura.

Componente en fase	Componente en cuadratura	Ángulo de fase\(\phi\)
\(>0\)	\(=0\)	\ (\ phi\)” class="lt-eng-7734">\(0^{\circ} \text { and } \mp 360^{\circ}\)
\(=0\)	\(<0\)	\ (\ phi\)” class="lt-eng-7734">\(-90^{\circ} \text { and }+270^{\circ}\)
\(<0\)	\(=0\)	\ (\ phi\)” class="lt-eng-7734">\(\mp 180^{\circ}\)
\(=0\)	\(>0\)	\ (\ phi\)” class="lt-eng-7734">\(-270^{\circ} \text { and }+90^{\circ}\)

También podría ser instructivo comparar la gráfica Nyquist de la Figura\(\PageIndex{1}\) con los componentes polares correspondientes para\(\zeta=0.2\) en las gráficas Bode modificadas de la Figura 10.2.1. En ambas cifras para\(\omega \approx 0\), la respuesta es esencialmente el valor estático,\(F R F(0)=+1+j 0\). A medida que la frecuencia\(\omega\) aumenta de\(0+\) a\(\omega_n\), la relación de magnitud varía (en su mayoría aumentando) de +1 a\(1 /(2 \zeta)=2.5\), mientras que el ángulo de fase, un retraso, varía de 0° a −90°. A\(\omega=\omega_{n}\), la respuesta es pura cuadratura negativa,\(F R F\left(\omega_{n}\right)=0-j 2.5\). A medida que\(\omega\) aumenta anteriormente\(\omega_n\), la relación de magnitud disminuye monótonamente mientras que la fase se queda aún más, con la relación de magnitud acercándose a cero y la fase aproximándose a −180° como\(\omega \rightarrow \infty\).

La respuesta de frecuencia del sistema estándar de ^{segundo orden amortiguado} positivamente se comporta bien, especialmente para, es decir\(\omega = 0\), una entrada distinta de cero que es constante en el tiempo, para lo cual el sistema tiene una salida estática constante distinta de cero incuestionablemente estable. Consideremos ahora el trazado Nyquist para un sistema de contraste, un sistema de bucle abierto que carece de una respuesta estática estable, el sistema de la Sección 17.1 (también Secciones 16.3, 16.5 y 16.6). La indicación más clara de una dificultad posible es la Ecuación 17.1.7 para\(\operatorname{OLFRF}(\omega)\), que indica una respuesta infinita para\(\omega = 0\). La fuente matemática de esta dificultad es el polo de\(O \operatorname{LTF}(s)\) en el origen\(s\) -plano, lo cual es evidente en la Ecuación 17.1.2, Figura 16.6.2, y en otras partes. La visualización gráfica de la magnitud de respuesta de frecuencia se vuelve muy grande como\(\omega \rightarrow 0\) es producida por los siguientes comandos de MATLAB, que calculan la respuesta de frecuencia y producen una gráfica Nyquist de la misma solución numérica que la de la Figura 17.1.3, para el caso de estabilidad neutra\(\Lambda=\Lambda_{n s}=40,000\) s ^-2:

>> wb=300; coj=100; wns=sqrt (wb*coj);

>> wbar=logspace (-1,1,200); w=wbar*wns;

>> lm=4e4; olfrf4e4=lm*wb. /(j*w.* (j*w+coj). * (j*w+wb));

>> parcela (real (olfrf4e4), imag (olfrf4e4)), rejilla

La figura\(\PageIndex{2}\) es una parte anotada del gráfico de MATLAB que muestra las características notables de la gráfica Nyquist. Esta gráfica muestra que para que la frecuencia sea\(\omega\) cada vez más pequeña, el componente de cuadratura negativa de respuesta se vuelve progresivamente más grande.

Figura\(\PageIndex{2}\): Gráfica Nyquist, Ecuación 17.1.7, respuesta de frecuencia para\(\Lambda=\Lambda_{n s}=40,000\) s ^-2 del sistema de bucle abierto en la Figura 17.1.2, con parámetros\(\omega_{b}=300\)\(c_{\theta} / J=100\) s ^-1^{, s -1} y\(\omega_{n s}=\sqrt{\omega_{b} \times c_{\theta} / J}=173.2\) rad/s. (Copyright; autor vía fuente)

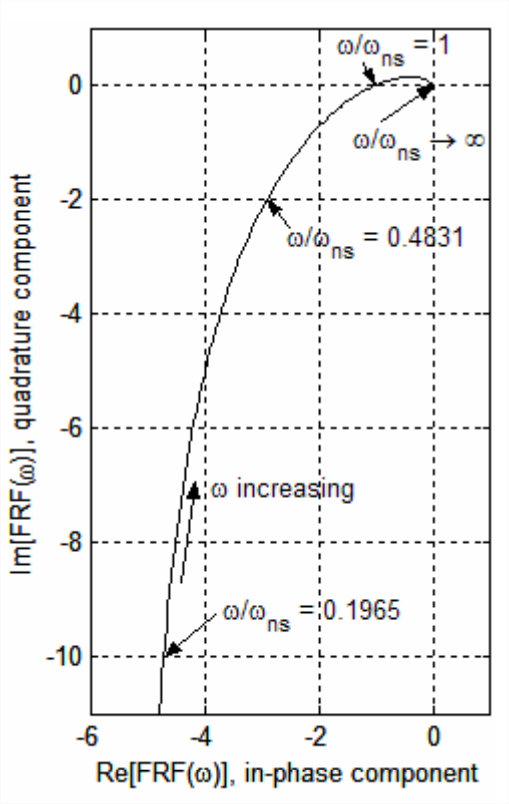
De hecho, podemos calcular a partir de la Ecuación 17.1.7 la naturaleza asintótica de la variación de la respuesta de frecuencia de bucle abierto\(\omega \rightarrow 0\), ya que, aplicando el método de división rectangular compleja descrito en la Sección 2.1:

\[O L F R F(\omega)=\frac{\Lambda \omega_{b}}{j \omega\left(j \omega+c_{\theta} / J\right)\left(j \omega+\omega_{b}\right)}=\frac{40,000 \times 300}{(j \omega)^{3}-(100+300) \omega^{2}+(100 \times 300) j \omega}=\frac{1.2 \times 10^{7} \times\left[-400 \omega^{2}-j\left(3 \times 10^{4} \omega-\omega^{3}\right)\right]}{9 \times 10^{8} \omega^{2}+1 \times 10^{5} \omega^{4}+\omega^{6}} \nonumber \]

Por lo tanto, como\(\omega \rightarrow 0\),

\[\operatorname{OLFRF}(\omega) \rightarrow \frac{1.2 \times 10^{7} \times\left[-400 \omega^{2}-j\left(3 \times 10^{4} \omega\right)\right]}{9 \times 10^{8} \omega^{2}}=-51 / 3-j \frac{400}{\omega}\label{eqn:17.13} \]