1.1: Primitivas de red

La teoría de redes eléctricas trata de dos cantidades primitivas, a las que nos referiremos como:

1. Potencial (o voltaje), y
2. Actual.

La corriente es el flujo real de portadores cargados, mientras que la diferencia de potencial es la fuerza que causa ese flujo. Como veremos, el potencial es una función de valor único que puede definirse de manera única sobre los nodos de una red. La corriente, por otro lado, fluye a través de las ramas de la red. La figura 1 muestra la noción básica de una rama, en la que se define una tensión a través de la rama y se define una corriente para fluir a través de la rama. Una red es una colección de tales elementos, conectados entre sí por cables.

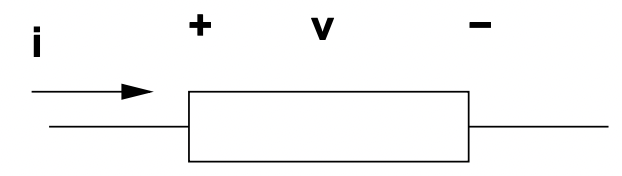Figura 1: Elemento básico del circuito

La topología de red es la interconexión de sus elementos. Eso, más las restricciones de tensión y corriente impuestas por los propios elementos, determina el rendimiento de la red, descrito por la distribución de voltajes y corrientes a lo largo de la red.

Dos conceptos importantes deben describirse inicialmente. Estos son de “loop” y “node”.

1. Un bucle en la red es cualquier ruta cerrada a través de dos o más elementos de la red. Cualquier red no trivial tendrá al menos un bucle de este tipo.

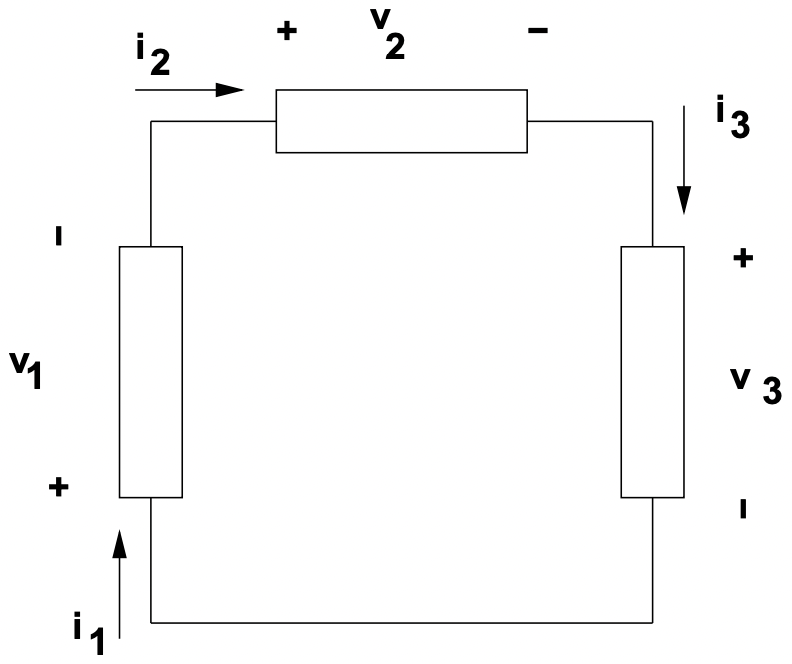Figura 2: Esto es un bucle

2. un nodo es un punto en el que dos o más elementos están interconectados.

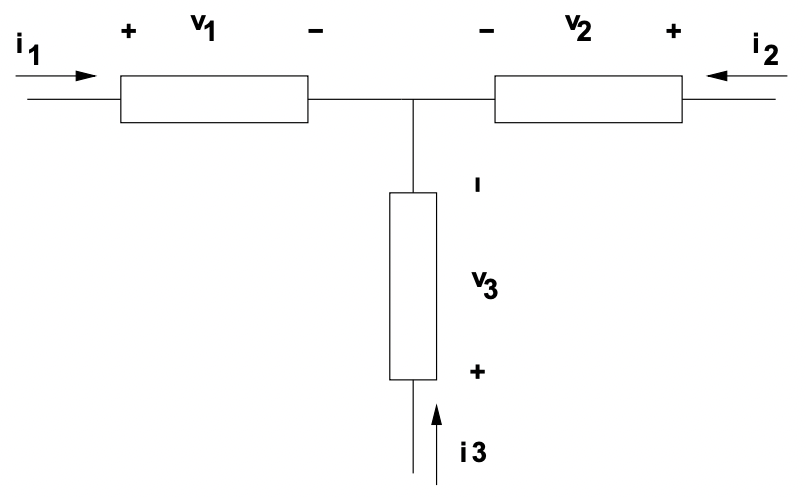Figura 3: Este es un nodo

Las dos leyes fundamentales de la teoría de redes se conocen como Ley de Voltaje de Kirchoff (KVL) y Ley de Corriente de Kirchoff (KCL). Estas leyes describen la topología de la red, y surgen directamente de las leyes fundmantales de la electromagnetica. Simplemente se declaran como:

• \(\ \sum_{l o o p} v_{k}=0 \label{1}\)
• \(\ \sum_{n o d e} i_{k}=0\label{2}\)

1Tenga en cuenta que KVL es una versión discreta de la Ley de Faraday, válida en la medida en que ningún flujo variable en el tiempo vincula el bucle. KCL es solo la conservación de la corriente, permitiendo que no se acumule carga en el nodo.

Los elementos de red afectan los voltajes y corrientes de una de tres maneras:

1. Las fuentes de voltaje limitan la diferencia de potencial entre sus terminales para que sea de algún valor fijo (el valor de la fuente).
2. Las fuentes de corriente limitan la corriente a través de la rama para que sea de algún valor fijo.
3. Todos los demás elementos imponen algún tipo de relación, ya sea lineal o no lineal, entre el voltaje transversal y la corriente a través de la rama.

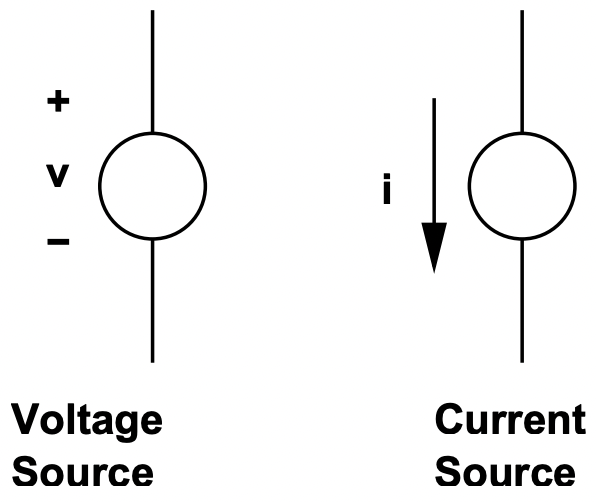Figura 4: Notación para fuentes de voltaje y corriente

Las fuentes de voltaje y corriente pueden ser independientes o dependientes. Las fuentes independientes tienen valores que son, como su nombre lo indica, independientes de otras variables en un circuito. Las fuentes dependientes tienen valores que dependen de alguna otra variable en un circuito. Un ejemplo común de una fuente dependiente es la fuente de corriente equivalente utilizada para modelar la unión del colector en un transistor. Por lo general, esta se modela como una fuente de corriente dependiente de la corriente, en la que se toma la corriente del colector para que dependa directamente de la corriente del emisor. Dichas fuentes dependientes deben manejarse con cierto cuidado, para ciertos trucos que estaremos discutiendo a continuación no trabajen con ellos.

Para la actualidad, consideraremos, además de las fuentes de tensión y corriente, solo elementos de impedancia, que imponen una relación lineal entre voltaje y corriente. El más común de estos es la resistencia, que impone la relación que a menudo se conoce como ley de Ohm:

\(\ v_{r}=R i_{r}\label{3}\)

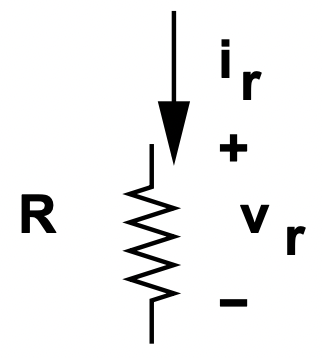Figura 5: Elemento de circuito de resistencia

Un poco más adelante en esta nota, extenderemos esta noción de impedancia a otros elementos, pero por el momento la resistencia servirá a nuestros propósitos.