1.6: Linealidad y superposición

Una noción extraordinariamente poderosa de la teoría de redes es la linealidad. Esta propiedad cuenta con dos elementos esenciales, declarados de la siguiente manera:

1. Para cualquier salida de\(\ x\) rendimiento de entrada única\(\ y\), la respuesta a una entrada\(\ k x\) es\(\ k y\) para cualquier valor de\(\ k\).
2. Si, en una red de entrada múltiple la entrada\(\ x_{1}\) por sí misma produce salida\(\ y_{1}\) y una segunda entrada\(\ x_{2}\) por sí misma produce\(\ y_{2}\), entonces la combinación de entradas\(\ x_{1}\) y\(\ x_{2}\) produce la salida\(\ y=y_{1}+y_{2}\).

Esto es importante para nosotros en este momento por dos razones:

1. Nos dice que la solución a ciertos problemas que involucran redes con múltiples entradas es en realidad más fácil de lo que podríamos esperar: si una red es lineal, podemos resolver para la salida con cada entrada separada, luego agregar las salidas. A esto se le llama superposición.
2. También nos dice que, para redes que son lineales, no es necesario considerar realmente el valor de las entradas en el cálculo de la respuesta. Lo importante es una función del sistema, o una relación de salida a entrada.

La superposición es un principio importante cuando se trata de redes lineales, y se puede utilizar para facilitar el análisis. Si una red tiene múltiples fuentes independientes, es posible encontrar la respuesta a cada fuente por separado, luego sumar todas las respuestas para encontrar la respuesta total. ¡Tenga en cuenta que esto solo se puede hacer con fuentes independientes!

Consideremos, por ejemplo, el circuito de ejemplo que se muestra en la Figura 12. Si solo nos interesa el voltaje de salida\(\ v_{2}\), podemos encontrar primero la respuesta a la fuente de voltaje, luego la respuesta a la fuente de corriente, entonces la respuesta total es la suma de los dos. Para encontrar la respuesta a la fuente de voltaje, debemos “apagar” la fuente de corriente. Esto se hace asumiendo que no está ahí. (¡Después de todo, una fuente de corriente con corriente cero es solo un circuito abierto!). La red resultante es como en la Figura 14.

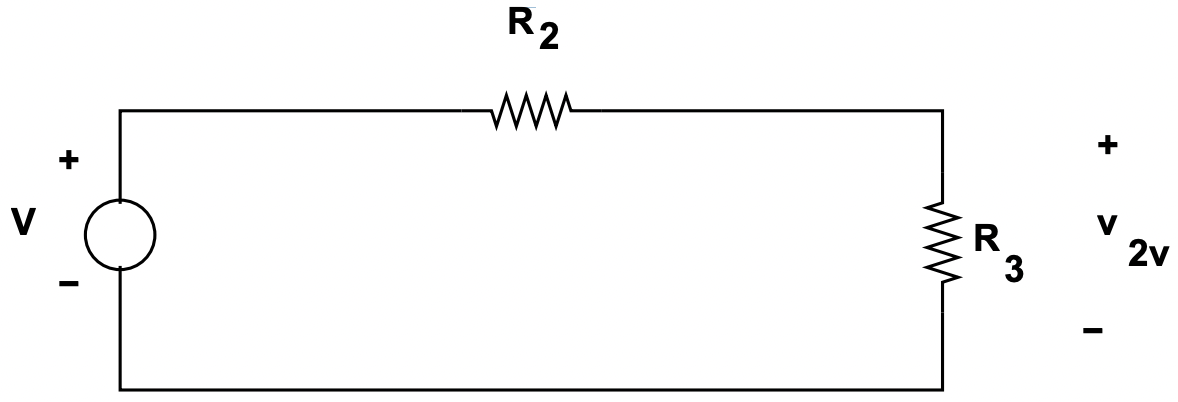Figura 14: Fragmento de superposición: Fuente de voltaje

Tenga en cuenta que la resistencia\(\ R_{1}\) no aparece aquí. Esto se debe a que una resistencia en paralelo con una fuente de voltaje es solo una fuente de voltaje, a menos que uno esté interesado en la corriente en la resistencia. El voltaje de salida es solo:

\(\ v_{2 v}=V \frac{R_{3}}{R_{2}+R_{3}}\)

A continuación, “apagamos” la fuente de voltaje y “encendemos” la fuente de corriente. Tenga en cuenta que una fuente de voltaje que ha sido apagada es un cortocircuito, porque eso implica voltaje cero. La red es como se muestra en la Figura 15

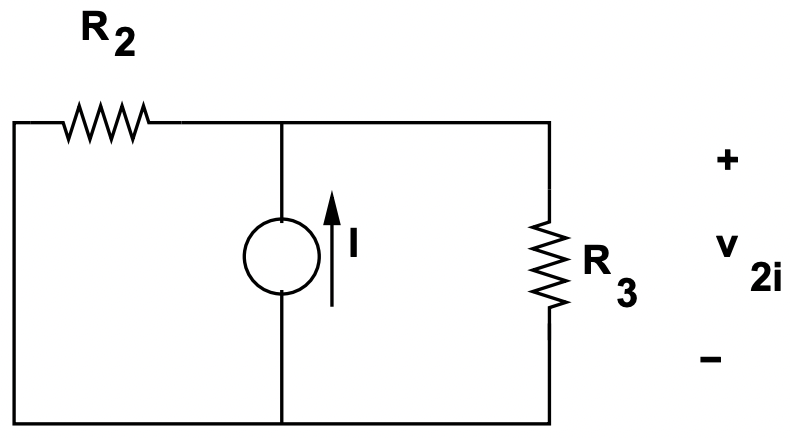Figura 15: Fragmento de superposición: Fuente de corriente

La respuesta a esto es:

\(\ v_{2 i}=I R_{2} \| R_{3}\)

La respuesta total es entonces solo:

\(\ v_{2}=v_{2 v}+v_{2 i}=V \frac{R_{3}}{R_{2}+R_{3}}+I \frac{R_{2} R_{3}}{R_{2}+R_{3}}\)