3.1: Dos Fases

El sistema bifásico es el más simple de todos los sistemas polifásicos de describir. Considere un par de fuentes de voltaje que se sientan una al lado de la otra con:

\[\ v_{1}=V \cos \omega t\label{1} \]

\(\ v_{2}=V \sin \omega t\label{2}\)

Supongamos que este sistema de fuentes está conectado a una “carga balanceada”, como se muestra en la Figura 1. Para calcular los flujos de potencia en el sistema, es conveniente reescribir los voltajes en forma compleja:

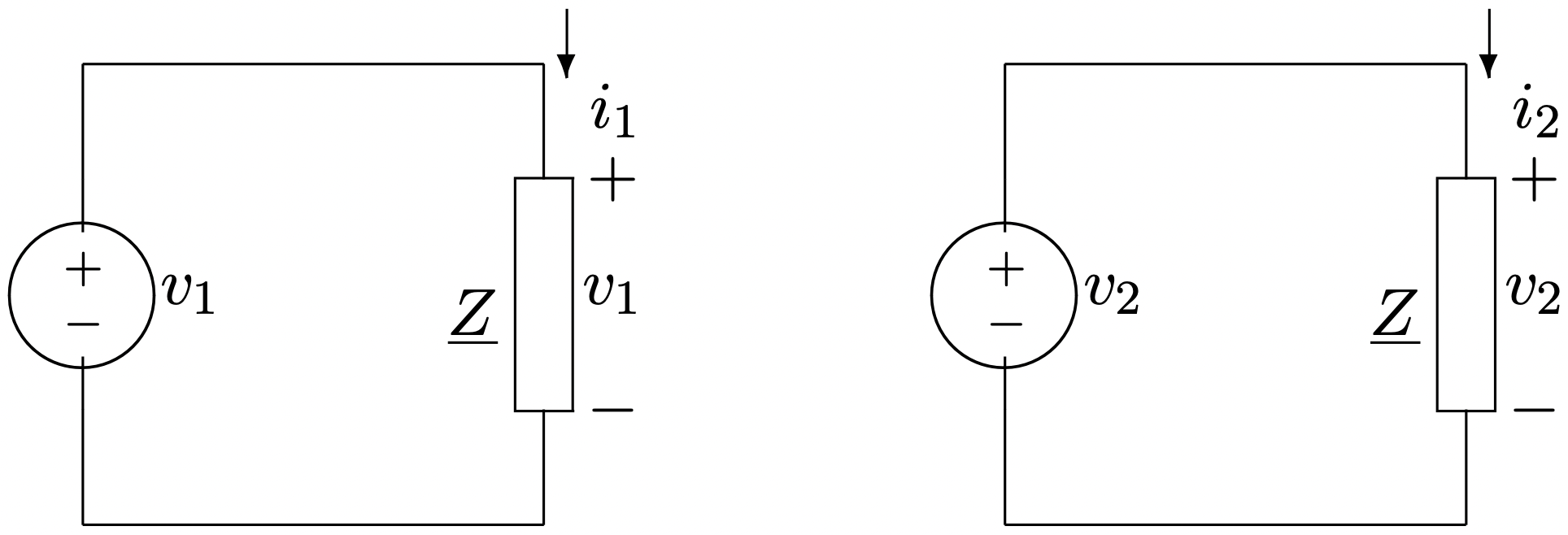Figura 1: Sistema bifásico

\(\ v_{1}=R e\left[\underline{V} e^{j \omega t}\right]\label{3}\)

\(\ v_{2}=R e\left[-j \underline{V} e^{j \omega t}\right]\label{4}\)

\(\ ={Re}\left[\underline{V} e^{j\left(\omega t-\frac{\pi}{2}\right)}\right]\label{5}\)

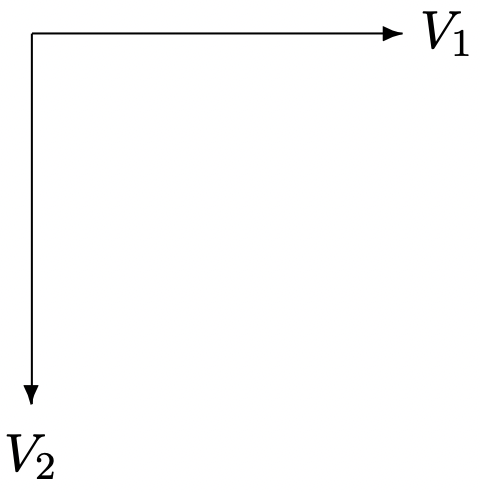Figura 2: Diagrama de fasores para fuente bifásica

Si cada fuente está conectada a una carga con impedancia:

\(\ \underline{Z}=|\underline{Z}| e^{j \psi}\)

entonces las amplitudes complejas de las corrientes son:

\ (\\ begin {array} {l}
\ subrayado {I} _ {1} =\ frac {\ subrayado {V}} {|\ subrayado {Z} |} e^ {-j\ psi}\
\ subrayado {I} _ _ {2} =\ frac {\ subrayado {V}} {|\ subrayado {Z} |} e^ {-j\ psi} ^ {-j\ frac {\ pi} {2}}
\ end {array}\)

Cada una de las redes bifásicas tiene el mismo valor para la potencia real y reactiva:

\(\ P+j Q=\frac{|\underline{V}|^{2}}{2|\underline{Z}|} e^{j \psi}\label{6}\)

o:

\(\ P=\frac{|\underline{V}|^{2}}{2|\underline{Z}|} \cos \psi\label{7}\)

\(\ Q=\frac{|\underline{V}|^{2}}{2|\underline{Z}|} \sin \psi\label{8}\)

La relación entre el “poder complejo” y el flujo de potencia instantáneo se desarrolló en el Capítulo 2 de estas notas. Para un sistema con voltaje de la forma:

\(\ v=R e\left[V e^{j \phi} e^{j \omega t}\right]\)

la potencia instantánea viene dada por:

\(\ p=P[1+\cos 2(\omega t+\phi)]+Q \sin 2(\omega t+\phi)\)

Para el caso aquí considerado,\(\ \phi=0\) para la fase 1 y\(\ \phi=-\frac{\pi}{2}\) para la fase 2. Así:

\ (\\ begin {array} {l}
p_ {1} =\ frac {|\ subrayado {V} |^ {2}} {2|\ subrayado {Z} |}\ cos\ psi [1+\ cos 2\ omega t] +\ frac {|\ subrayado {V} |^ {2}} {2|\ subrayado {Z} |}\ sin\ psi\ sin\ omega t\\
p_ {2} =\ frac {|\ subrayado {V} |^ {2}} {2|\ subrayado {Z} |}\ cos\ psi [1+\ cos (2\ omega t-\ pi)] +\ frac {|\ subrayado {V} |^ { 2}} {2|\ subrayado {Z} |}\ sin\ psi\ sin (2\ omega t-\ pi)
\ end {array}\)

Tenga en cuenta que las partes variables en el tiempo de estas dos expresiones tienen signos opuestos. Sumados, dan potencia instantánea:

\(\ p=p_{1}+p_{2}=\frac{|\underline{V}|^{2}}{|\underline{Z}|} \cos \psi\)

Al menos una de las ventajas de las redes de energía polifásica es ahora evidente. El uso de un sistema polifásico equilibrado evita las pulsaciones del flujo de potencia debido a la tensión y corriente de CA, e incluso las pulsaciones debidas al flujo de energía reactiva. Esto tiene beneficios obvios cuando se trata de motores y generadores o, de hecho, cualquier tipo de fuente o carga que quisiera ver potencia constante.