3.2: Sistemas trifásicos

Consideremos ahora la disposición de tres fuentes de voltaje ilustradas en la Figura 3.

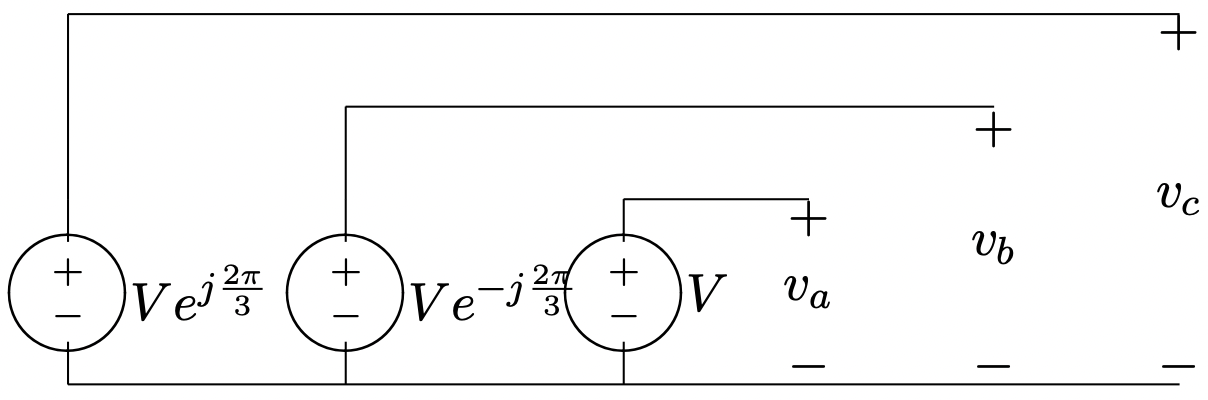Figura 3: Fuente de voltaje trifásico

Los voltajes trifásicos son:

\[\ v_{a}=\quad V \cos \omega t \quad=R e\left[V e^{j \omega t}\right]\label{9} \]

\[\ v_{b}=V \cos \left(\omega t-\frac{2 \pi}{3}\right)=R e\left[V e^{j\left(\omega t-\frac{2 \pi}{3}\right)}\right]\label{10} \]

\[\ v_{c}=V \cos \left(\omega t+\frac{2 \pi}{3}\right)=\operatorname{Re}\left[V e^{j\left(\omega t+\frac{2 \pi}{3}\right)}\right]\label{11} \]

Estos voltajes trifásicos se ilustran en el dominio del tiempo en la Figura 4 y como fasores complejos en la Figura 5. Observe el espaciado simétrico en el tiempo de los voltajes. Como en ejemplos anteriores, los voltajes instantáneos pueden visualizarse imaginando la Figura 5 girando en sentido antihorario con velocidad angular\(\ \omega\). Los voltajes instantáneos son solo proyecciones de los vectores de este “molinete” sobre el eje horizontal.

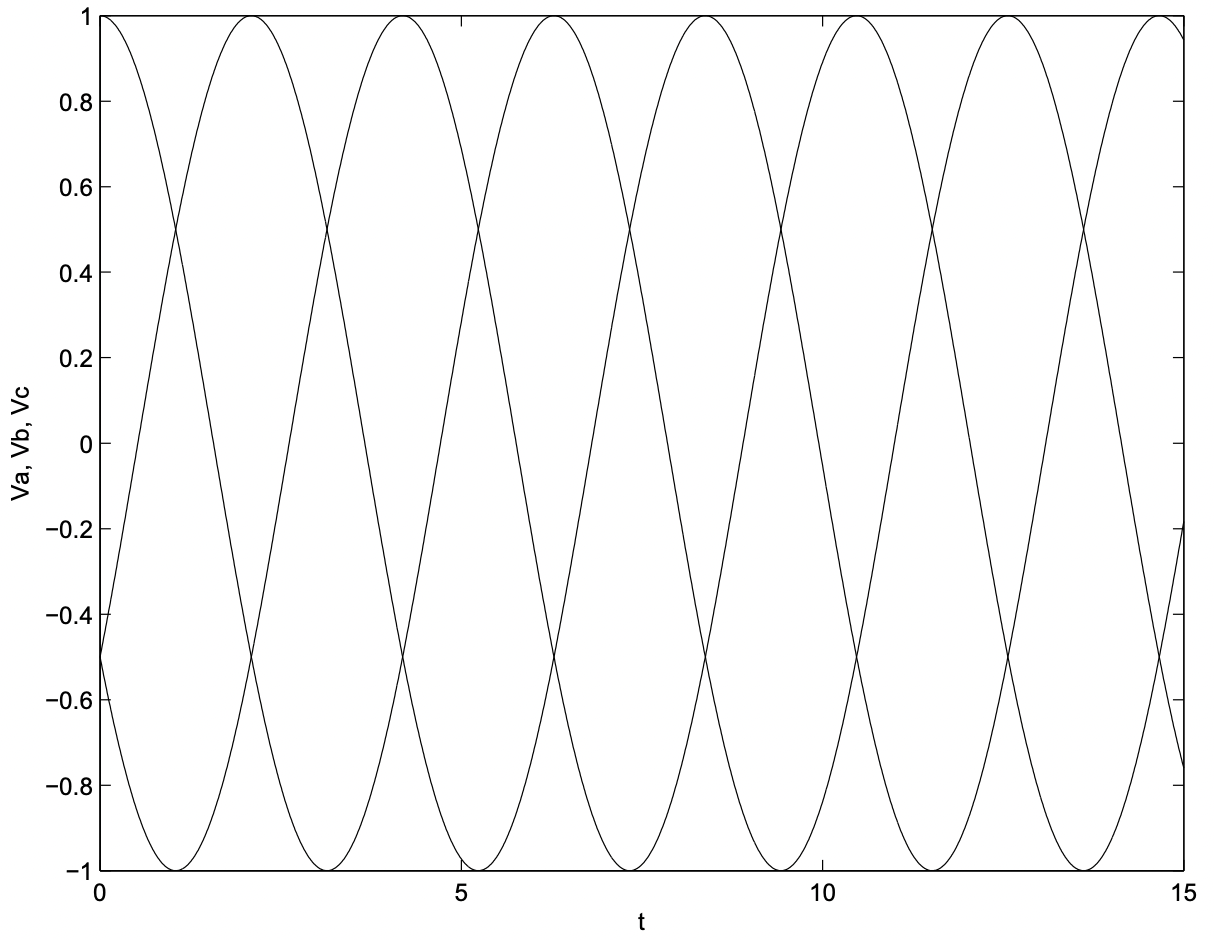Figura 4: Voltajes trifásicos

Considera conectar estas tres fuentes de voltaje a tres cargas idénticas, cada una con impedancia compleja\(\ \underline{Z}\), como se muestra en la Figura 6.

Si los voltajes son los dados por (9 - 11), entonces las corrientes en las tres fases son:

\[\ i_{a}=R e\left[\frac{\underline{\underline{V}}}{\underline{Z}} e^{j \omega t}\right]\label{12} \]

\[\ i_{b}=\operatorname{Re}\left[\frac{\underline{V}}{\underline{Z}} e^{j\left(\omega t-\frac{2 \pi}{3}\right)}\right]\label{13} \]

\[\ i_{c}=R e\left[\frac{\underline{V}}{\underline{Z}} e^{j\left(\omega t+\frac{2 \pi}{3}\right)}\right]\label{14} \]

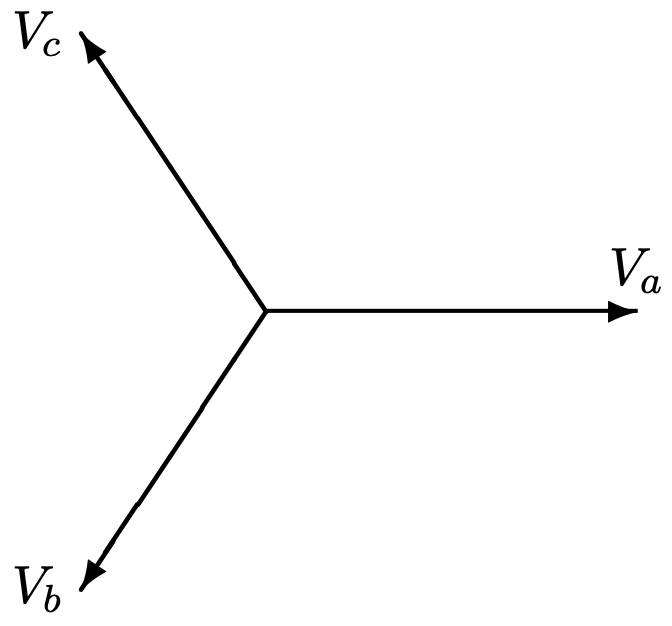Figura 5: Diagrama de fasores: voltajes trifásicos

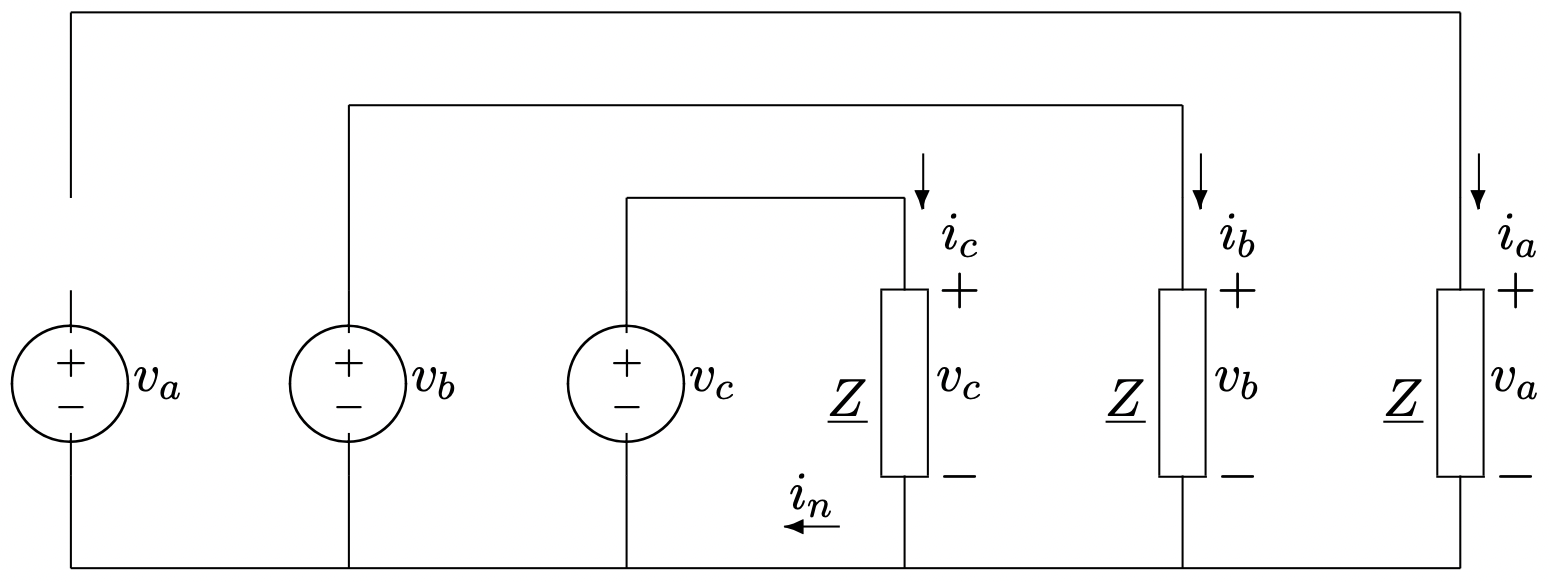Figura 6: Fuente trifásica conectada a carga balanceada

El poder complejo en cada una de las tres fases es:

\[\ P+j Q=\frac{|\underline{V}|^{2}}{2|\underline{Z}|}(\cos \psi+j \sin \psi)\label{15} \]

Entonces, recordando la fase temporal de las tres fuentes, es posible escribir los valores de potencia instantánea en las tres fases:

\[\ p_{a}=\frac{|\underline{V}|^{2}}{2|\underline{Z}|}\{\cos \psi[1+\cos 2 \omega t]+\sin \psi \sin 2 \omega t\}\label{16} \]

\[\ p_{b}=\frac{|\underline{V}|^{2}}{2|\underline{Z}|}\left\{\cos \psi\left[1+\cos \left(2 \omega t-\frac{2 \pi}{3}\right)\right]+\sin \psi \sin \left(2 \omega t-\frac{2 \pi}{3}\right)\right\}\label{17} \]

\[\ p_{c}=\frac{|\underline{V}|^{2}}{2|\underline{Z}|}\left\{\cos \psi\left[1+\cos \left(2 \omega t+\frac{2 \pi}{3}\right)\right]+\sin \psi \sin \left(2 \omega t+\frac{2 \pi}{3}\right)\right\}\label{18} \]

La suma de estas tres expresiones es la potencia instantánea total, que es constante:

\[\ p=p_{a}+p_{b}+p_{c}=\frac{3}{2} \frac{|\underline{V}|^{2}}{|\underline{Z}|} \cos \psi\label{19} \]

Es útil, al tratar con sistemas trifásicos, recordar que

\(\ \cos x+\cos \left(x-\frac{2 \pi}{3}\right)+\cos \left(x+\frac{2 \pi}{3}\right)=0\)

independientemente del valor de\(\ x\).

Ahora considere la corriente en el cable neutro,\(\ i_{n}\) en la Figura 6. Esta corriente viene dada por:

\[\ i_{n}=i_{a}+i_{b}+i_{c}=R e\left[\frac{V}{\underline{Z}}\left(e^{j \omega t}+e^{j\left(\omega t-\frac{2 \pi}{3}\right)}+e^{j\left(\omega t+\frac{2 \pi}{3}\right)}\right)\right]=0\label{20} \]

Esto muestra la ventaja más importante de los sistemas trifásicos sobre los sistemas bifásicos: un cable sin corriente en él no tiene que ser muy grande. De hecho, la conexión neutra puede eliminarse por completo en muchos casos. La red que se muestra en la Figura 7 funcionará así como la red de la Figura 6 en la mayoría de los casos en los que se equilibran las tensiones e impedancias de carga.

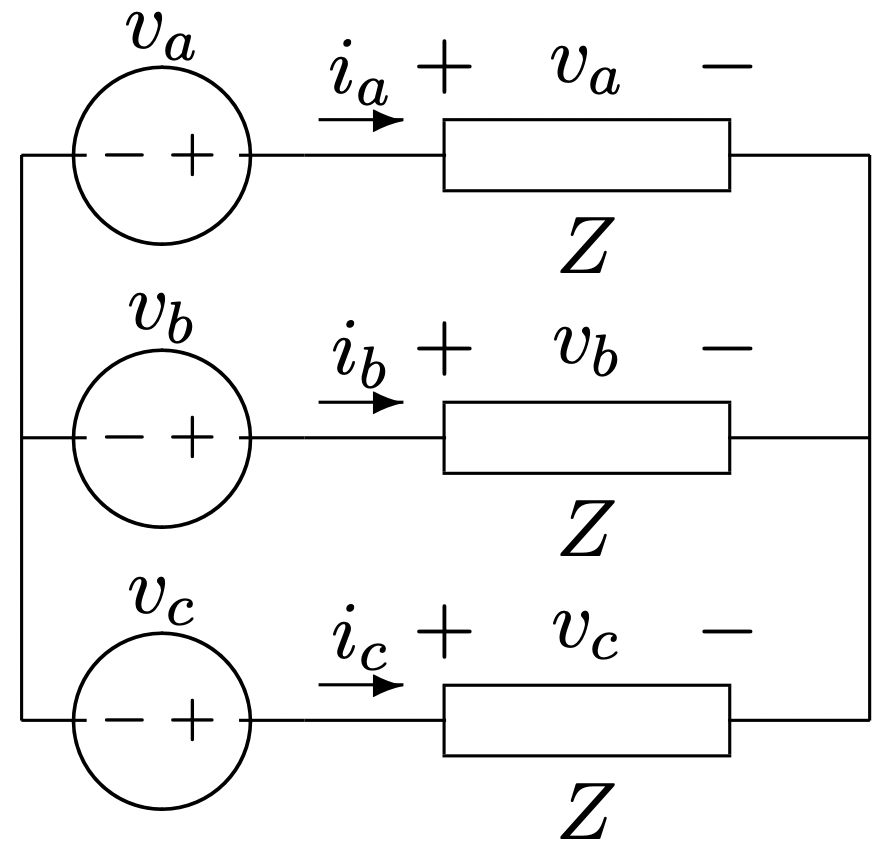Figura 7: Fuente y carga trifásicas sin conexión a tierra

Existe una diferencia fundamental entre sistemas conectados a tierra y no conectados a tierra si no se mantienen condiciones perfectamente equilibradas. En efecto, el cable de tierra proporciona aislamiento entre las fases al fijar el voltaje neutro a la punta de estrella para que sea cero. Si las impedancias de carga no son iguales, se dice que la carga está desequilibrada. Si el sistema está conectado a tierra habrá corriente en el neutro. Si una carga desequilibrada no está puesta a tierra, el voltaje de punto estrella no será cero, y los voltajes serán diferentes en las tres fases en la carga, incluso si todas las fuentes de voltaje tienen la misma magnitud.