3.3: Voltajes de línea

Un conjunto trifásico equilibrado de voltajes tiene un conjunto bien definido de voltajes de línea de línea. Si los voltajes de toneutrales de línea están dados por (9 - 11), entonces los voltajes de línea son:

\[\ v_{a b}=v_{a}-v_{b}=\operatorname{Re}\left[\underline{V}\left(1-e^{-j \frac{2 \pi}{3}}\right) e^{j \omega t}\right]\label{21} \]

\[\ v_{b c}=v_{b}-v_{c}=\operatorname{Re}\left[\underline{V}\left(e^{-j \frac{2 \pi}{3}}-e^{j \frac{2 \pi}{3}}\right) e^{j \omega t}\right]\label{22} \]

\[\ v_{c a}=v_{c}-v_{a}=R e\left[\underline{V}\left(e^{j \frac{2 \pi}{3}}-1\right) e^{j \omega t}\right]\label{23} \]

y estos reducen a:

\[\ v_{a b}=\operatorname{Re}\left[\sqrt{3} \underline{V} e^{j \frac{\pi}{6}} e^{j \omega t}\right]\label{24} \]

\[\ v_{b c}=R e\left[\sqrt{3} \underline{V} e^{-j \frac{\pi}{2}} e^{j \omega t}\right]\label{25} \]

\[\ v_{c a}=\operatorname{Re}\left[\sqrt{3} \underline{V} e^{j \frac{5 \pi}{6}} e^{j \omega t}\right]\label{26} \]

La relación fasor de los voltajes de línea a neutro y línea a línea se muestra en la Figura 8. Hay que señalar dos cosas sobre esta relación:

• El conjunto de voltaje de línea a línea tiene una magnitud que es mayor que el voltaje de línea a tierra en un factor de\(\ \sqrt{3}\).
• Los voltajes de línea a línea se desplazan en fase 30 ^o por delante de los voltajes de línea a neutro.

Claramente, los voltajes de línea a línea forman un conjunto trifásico al igual que los voltajes de línea a neutro. Los componentes del sistema de alimentación (fuentes, devanados del transformador, cargas, etc.) pueden estar conectados entre líneas y neutro o entre líneas. La primera conexión de muchas veces llamada wye, esta última se llama delta, por razones obvias.

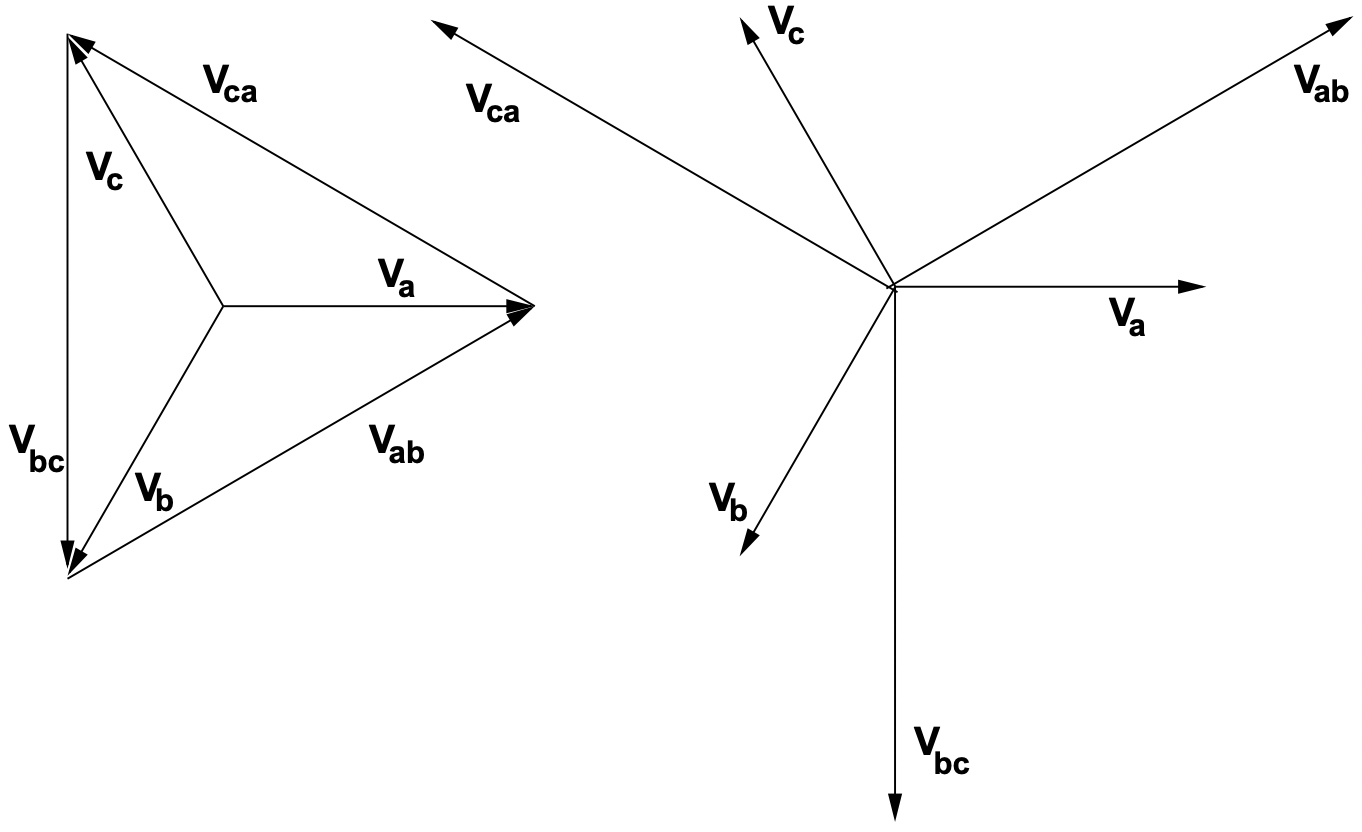Figura 8: Tensiones de línea neutra y línea-línea

Cabe señalar que la conexión Wye es al menos potencialmente una conexión de cuatro terminales, mientras que la conexión delta es inherentemente de tres terminales. La diferencia es la disponibilidad de un punto neutro. En condiciones de operación balanceadas esto no es importante, pero la diferencia es aparente e importante en condiciones desequilibradas.

Ejemplo: Cargas conectadas en Wye y Delta

Las cargas se pueden conectar en configuración de línea a neutro o de línea a línea. Un ejemplo del uso de esta flexibilidad es en un sistema de distribución de uso bastante común con un voltaje de línea a neutro de 120 V, RMS. En este sistema el voltaje línea a línea es de 208 V, RMS. Las cargas monofásicas se pueden conectar de línea a línea o de línea a neutro.

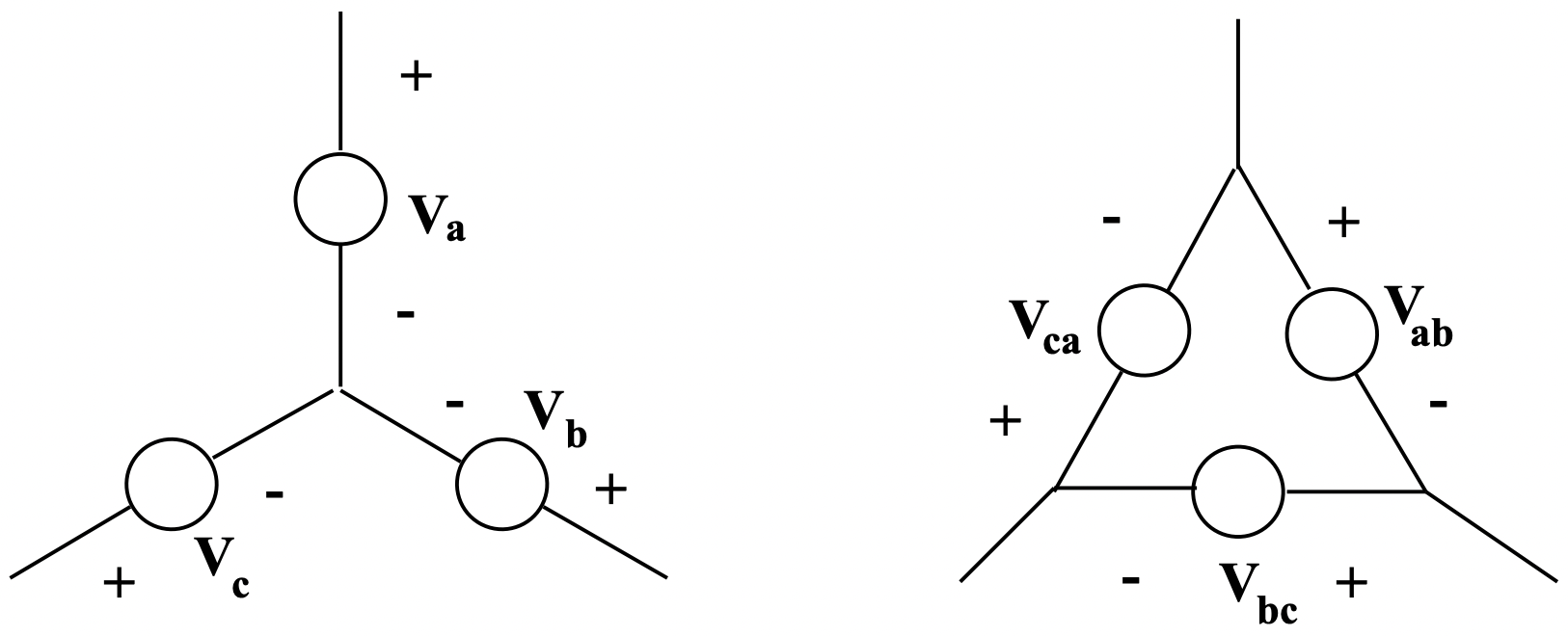Figura 9: Fuentes de voltaje conectadas en Wye y Delta

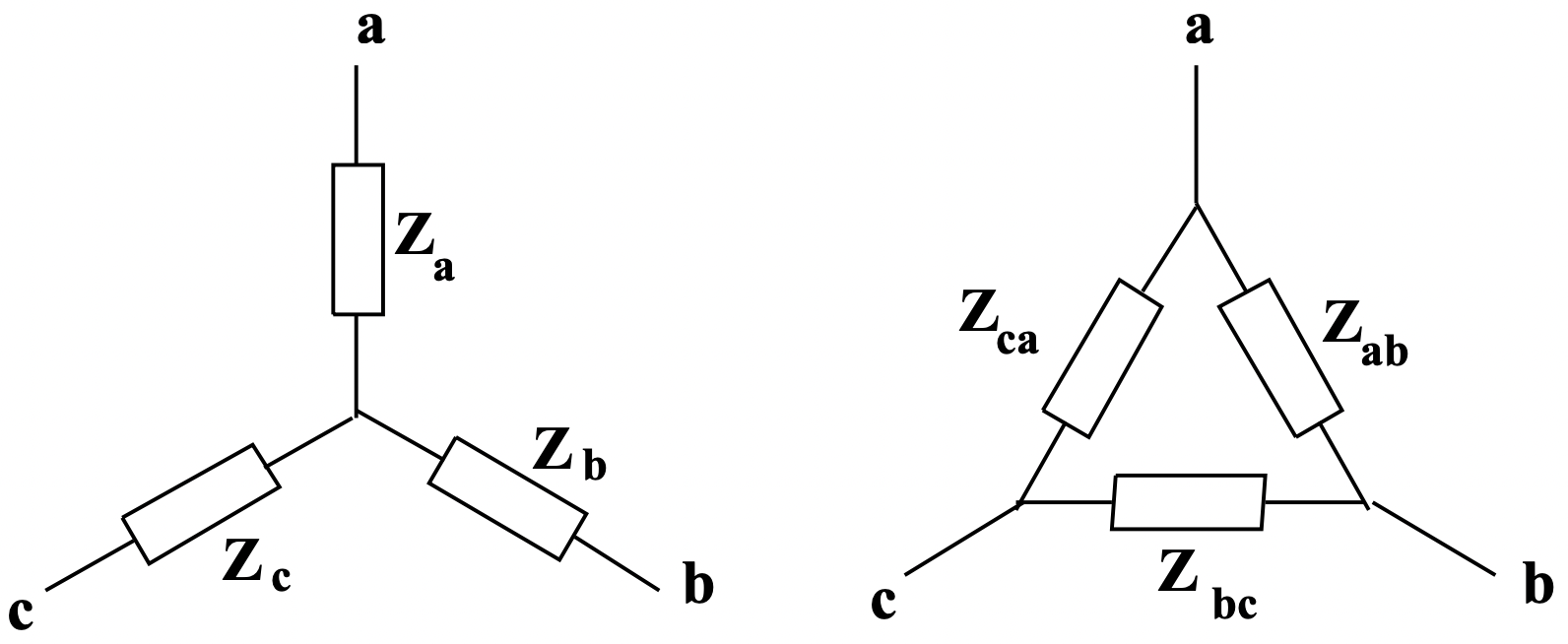Figura 10: Impedancias conectadas en Wye y Delta

Supongamos que es necesario construir un calentador resistivo para entregar 6 kW, para estar hecho de tres elementos los cuales pueden estar conectados ya sea en wye o delta. Cada uno de los tres elementos debe disipar 2000 W.

Así, ya que\(\ P=\frac{V^{2}}{R}\), las resistencias conectadas en forma de Wye serían:

\(\ R_{y}=\frac{120^{2}}{2000}=7.2 \Omega\)

mientras que las resistencias conectadas delta serían:

\(\ R_{\Delta}=\frac{208^{2}}{2000}=21.6 \Omega\)

Como sugiere este ejemplo, las impedancias conectadas en wye y delta suelen ser directamente equivalentes. De hecho, las conexiones no puestas a tierra son redes de tres terminales que pueden representarse de dos maneras. Las dos redes mostradas en la Figura 10, combinaciones de tres impedancias pasivas, son directamente equivalentes e idénticas en su comportamiento terminal si las relaciones entre elementos son las dadas en (27 - 32).

\[\ \underline{Z}_{a b}=\frac{\underline{Z}_{a} \underline{Z}_{b}+\underline{Z}_{b} \underline{Z}_{c}+\underline{Z}_{c} \underline{Z}_{a}}{\underline{Z}_{c}}\label{27} \]

\[\ \underline{Z}_{b c}=\frac{\underline{Z}_{a} \underline{Z}_{b}+\underline{Z}_{b} \underline{Z}_{c}+\underline{Z}_{c} \underline{Z}_{a}}{\underline{Z}_{a}}\label{28} \]

\[\ \underline{Z}_{c a}=\frac{\underline{Z}_{a} \underline{Z}_{b}+\underline{Z}_{b} \underline{Z}_{c}+\underline{Z}_{c} \underline{Z}_{a}}{\underline{Z}_{b}}\label{29} \]

\[\ \underline{Z}_{a}=\frac{\underline{Z}_{a b} \underline{Z}_{c a}}{\underline{Z}_{a b}+\underline{Z}_{b c}+\underline{Z}_{c a}}\label{30} \]

\[\ \underline{Z}_{b}=\frac{\underline{Z}_{a b} \underline{Z}_{b c}}{\underline{Z}_{a b}+\underline{Z}_{b c}+\underline{Z}_{c a}}\label{31} \]

\[\ \underline{Z}_{c}=\frac{\underline{Z}_{b c} \underline{Z}_{c a}}{\underline{Z}_{a b}+\underline{Z}_{b c}+\underline{Z}_{c a}}\label{32} \]

Un caso especial de la equivalencia wye-delta es el de cargas balanceadas, en el que:

\(\ \underline{Z}_{a}=\underline{Z}_{b}=\underline{Z}_{c}=\underline{Z}_{y}\)

y

\(\ \underline{Z}_{a b}=\underline{Z}_{b c}=\underline{Z}_{c a}=\underline{Z}_{\Delta}\)

en cuyo caso:

\(\ \underline{Z}_{\Delta}=3 \underline{Z}_{y}\)

Ejemplo: Uso de Wye-Delta para cargas desequilibradas

La carga desequilibrada mostrada en la Figura 11 está conectada a una fuente de voltaje balanceada. El problema es determinar las corrientes de línea. Tenga en cuenta que su carga está desconectada a tierra (si estuviera conectada a tierra, esto sería un problema trivial). Los voltajes vienen dados por:

\ (\\ begin {array} {l}
v_ {a} =V\ cos\ omega t\\
v_ {b} =V\ cos\ izquierda (\ omega t-\ frac {2\ pi} {3}\ derecha)\\
v_ {c} =V\ cos\ izquierda (\ omega t+\ frac {2\ pi} {3}\ derecha)
\ end array}\)

Para resolver este problema, convierta tanto la fuente como la carga a conexiones equivalentes delta, como se muestra en la Figura 12. Los valores de las tres resistencias son:

\ (\\ begin {array} {c}
r_ {a b} =r_ {c a} =\ frac {2+4+2} {2} =4\\
r_ {b c} =\ frac {2+4+2} {1} =8
\ end {array}\)

Las amplitudes complejas de las fuentes de voltaje equivalentes son:

\ (\\ begin {array} {ll}
\ subrayado {V} _ _ {a b} &=\ subrayado {V} _ {a} -\ subrayado {V} _ {b} =\ subrayado {V}\ left (1-e^ {-j\ frac {2\ pi} {3}}\ derecha) &=\ subrayado {V}\ sqrt {3} e^ {j\ frac {\ pi} {6}}\
\ subrayado {V} _ {b c} &=\ subrayado {V} _ {b} -\ subrayado {V} _ _ {c} =\ subrayado {V}\ izquierda (e^ {-j\ frac {2\ pi} {3}} -e^ {j\ frac {2\ pi} {3}}\ derecha) &=\ subrayado {V}\ sqrt {3} e^ {-j\ frac {\ pi} {2}}\
\ subrayado {V} _ {c a} &=\ subrayado {V} _ _ {c} -\ subrayado {V} _ {a} = subrayado {V}\ izquierda (e^ {j\ frac {2\ pi} {3}} -1\ derecha) &=\ subrayado {V}\ sqrt {3} e^ {j\ frac {5\ pi} {6}}
\ end {array}\)

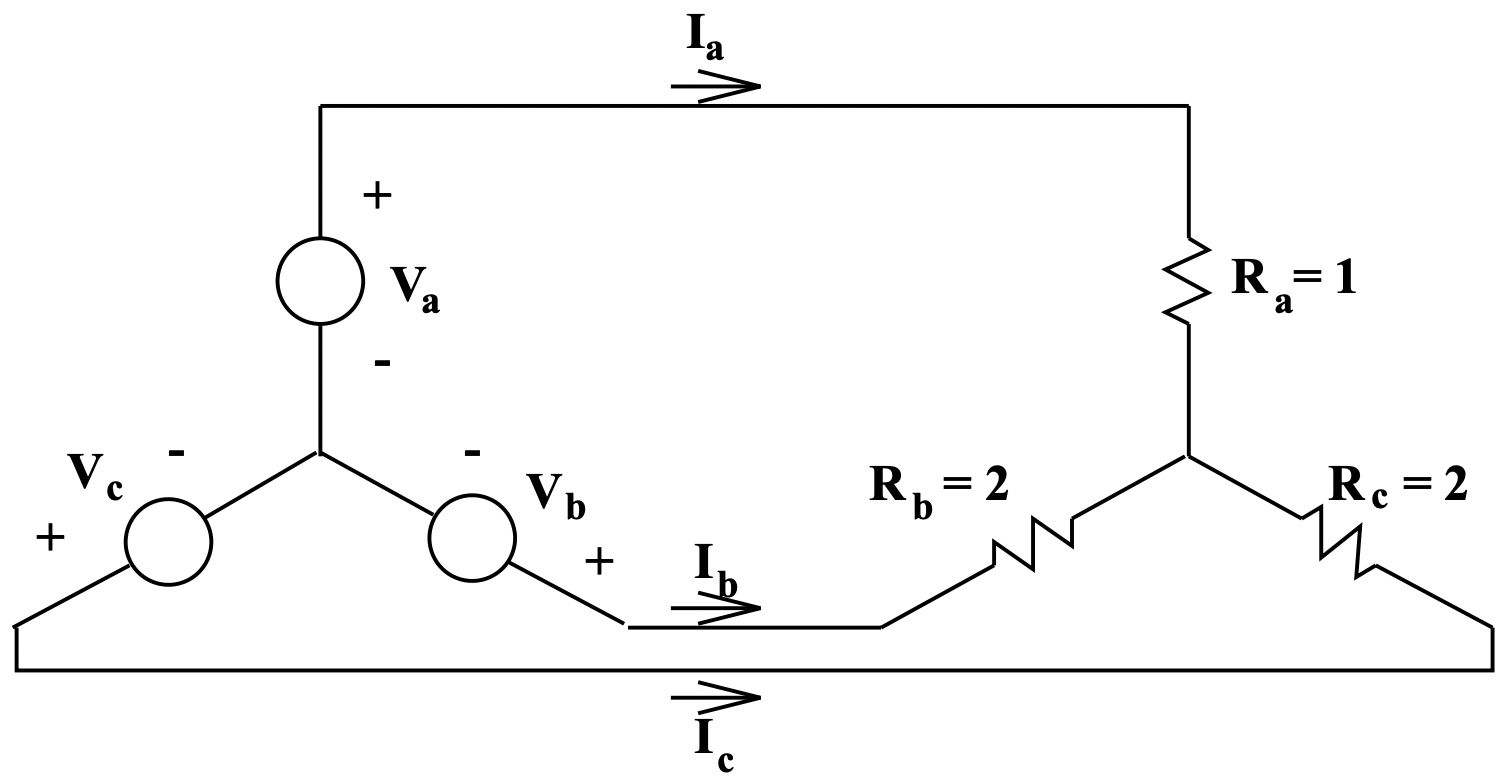Figura 11: Carga desequilibrada

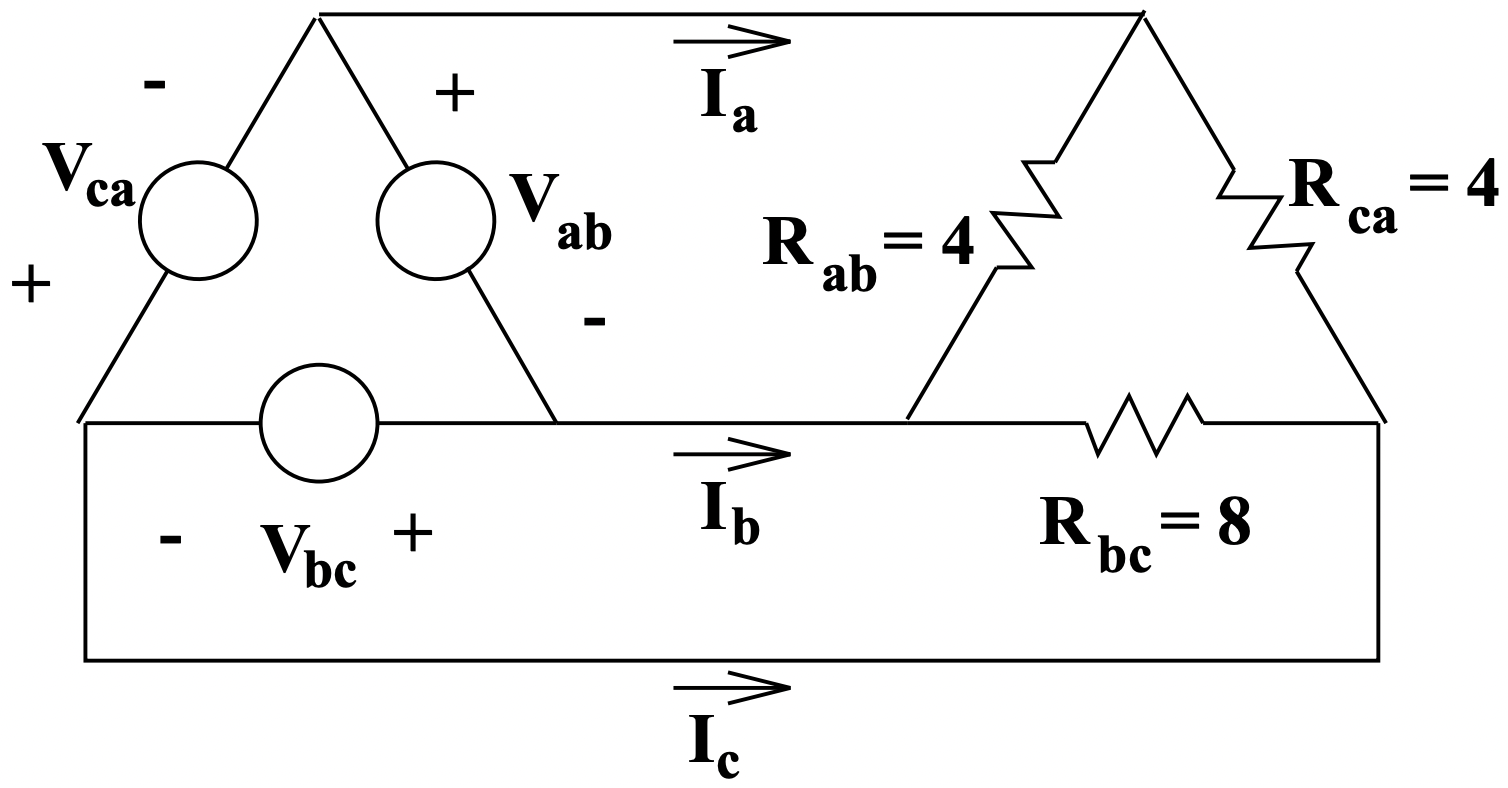Figura 12: Equivalente a Delta

Las corrientes en cada una de las resistencias equivalentes son:

\(\ \underline{I}_{1}=\frac{\underline{V}_{a b}}{r_{a b}} \quad \underline{I}_{2}=\frac{\underline{V}_{b c}}{r_{b c}} \quad \underline{I}_{3}=\frac{V_{c a}}{r_{c a}}\)

Los curentes de línea son entonces solo la diferencia entre la corriente en las piernas del delta:

\ (\\ begin {array} {l}
I_ {a} =I_ {1} -I_ {3} =\ sqrt {3} V\ left (\ frac {e^ {j\ frac {\ pi} {6}}} {4} -\ frac {e^ {j\ frac {5\ pi} {6}} {4}\ derecha) =\ frac {3} {4} V\\
I_ {b} =I_ {2} -I_ {1} =\ sqrt {3} V\ izquierda (\ frac {e^ {-j\ frac {\ pi} {2}}} {8} -\ frac {e^ {j}\ frac {\ pi} {6}} {4}\ derecha) =-\ izquierda (\ frac {3} {8} +j\ frac {1} {4}\ derecha) V \\
I_ {c} =I_ {3} -I_ {2} =\ sqrt {3} V\ izquierda (\ frac {e^ {5\ frac {5\ pi} {6}}} {4} -\ frac {e^ {-j\ frac {\ pi} {2}}} {8}\ derecha) =-\ izquierda (\ frac {3} 8} -j\ frac {1} {4}\ derecha) V
\ end {array}\)

Estos se muestran en la Figura 13.

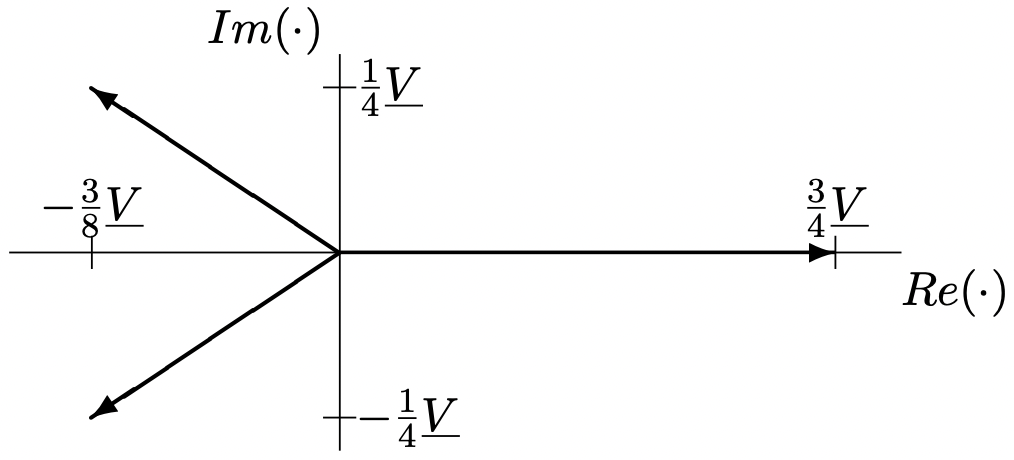Figura 13: Corrientes de línea