3.5: Transformadores trifásicos

Un transformador trifásico es simplemente tres transformadores monofásicos. La complicación en estas cosas es que hay una serie de formas de enrollarlas, y una serie de formas de interconectarlas. Tendremos más que decir sobre los devanados más adelante. Por ahora, considere las interconexiones. En cualquiera de los “lados” de una conexión de transformador (es decir, los lados de alto voltaje y bajo voltaje), es posible conectar devanados de transformador ya sea de línea a neutro (wye) o de línea a línea (delta). Así podemos hablar de conexiones de transformadores siendo wye-wye, delta-delta, wye-delta o delta-wye.

Ignorando ciertas complicaciones de las que tendremos más que decir en breve, la conexión de transformadores en wye-wye o delta-delta es razonablemente fácil de entender. Cada uno de los voltajes de línea a neutro (en el caso de wye-wye) o línea a línea (en el caso de delta-delta) se transforma por uno de los tres transformadores. Por otro lado, las interconexiones de un transformador wye-delta o delta-wye son un poco más complejas. La Figura 16 muestra una conexión delta-wye, en lo que podría llamarse forma de “diagrama de cableado”. En la Figura 17 se muestra una forma más esquemática (y más común) de la misma imagen. En esa imagen, los elementos devanados que aparecen paralelos se enrollan en el mismo segmento de núcleo, y así constituyen un transformador monofásico.

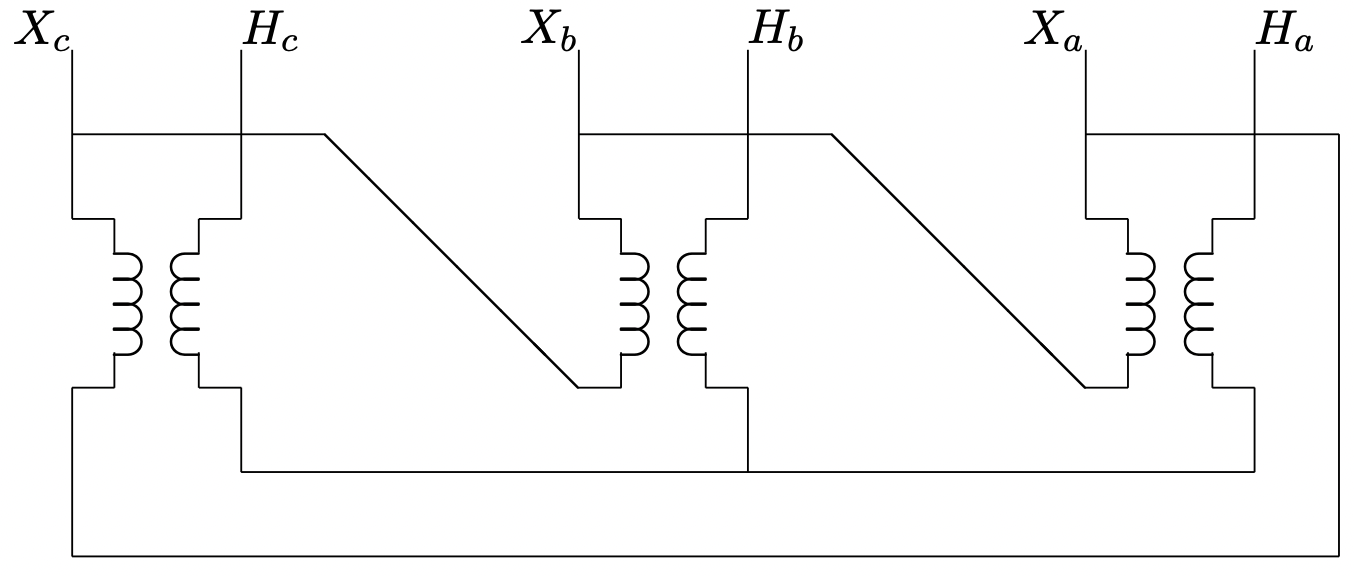Figura 16: Conexión del transformador Delta-Wye

Ahora: asuma eso\(\ N_{\Delta}\) y\(\ N_{Y}\) son números de giros. Si se considera que los transformadores individuales son ideales, existen las siguientes restricciones de voltaje y corriente:

\[\ v_{a Y}=\frac{N_{Y}}{N_{\Delta}}\left(v_{a \Delta}-v_{b \Delta}\right)\label{37} \]

\[\ v_{b Y}=\frac{N_{Y}}{N_{\Delta}}\left(v_{b \Delta}-v_{c \Delta}\right)\label{38} \]

\[\ v_{c Y}=\frac{N_{Y}}{N_{\Delta}}\left(v_{c \Delta}-v_{a \Delta}\right)\label{39} \]

\[\ i_{a \Delta}=\frac{N_{Y}}{N_{\Delta}}\left(i_{a Y}-i_{c Y}\right)\label{40} \]

\[\ i_{b \Delta}=\frac{N_{Y}}{N_{\Delta}}\left(i_{b Y}-i_{a Y}\right)\label{41} \]

\[\ i_{c \Delta}=\frac{N_{Y}}{N_{\Delta}}\left(i_{c Y}-i_{b Y}\right)\label{42} \]

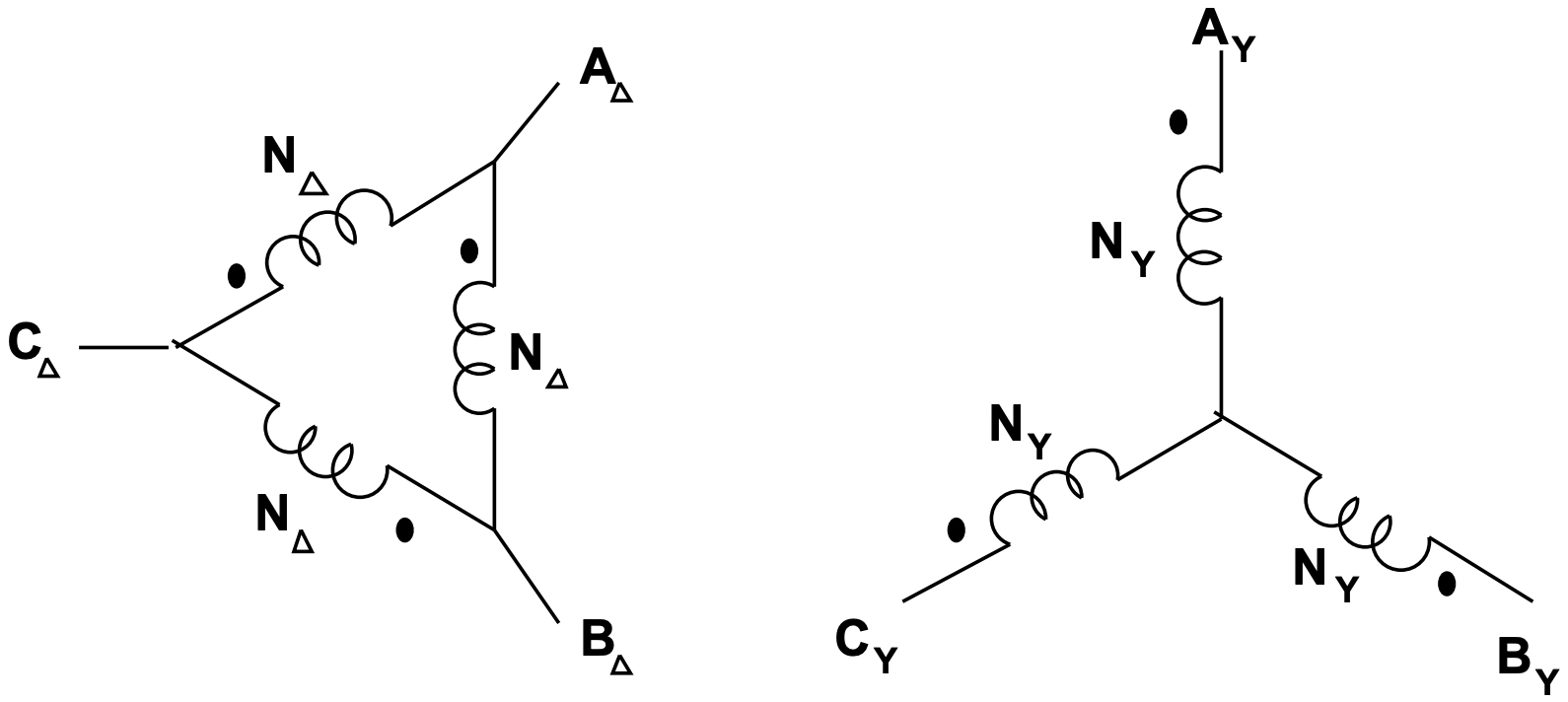Figura 17: Esquema de la conexión del transformador Delta-Wye

donde cada una de las tensiones es neutra de línea y las corrientes están en las líneas en los terminales del transformador.

Ahora, considere lo que sucede si un\(\ \Delta-Y\) transformador está conectado a una fuente de voltaje trifásico balanceada, de manera que:

\ (\\ begin {array} {l}
v_ {a\ Delta} =R e\ izquierda (\ subrayado {V} e^ {j\ omega t}\ derecha)\\
v_ {b\ Delta} =\ nombreoperador {Re}\ izquierda (\ subrayado {V} e^ {j\ izquierda (\ omega t-\ frac {2\ pi} {3}\ derecha)}\ derecha)\\
v_ {c\ Delta} =\ nombreoperador {Re}\ izquierda (\ subrayado {V} e^ {j\ izquierda (\ omega t+\ frac {2\ pi} {3} \ derecha)}\ derecha)
\ end {array}\)

Entonces, amplitudes complejas en el\(\ wye\) costado son:

\ (\\ begin {array} {ll}
\ subrayado {V} _ _ {a Y} = &\ frac {N_ {Y}} {N_ {\ Delta}}\ subrayado {V}\ izquierda (1-e^ {-j\ frac {2\ pi} {3}}\ derecha) = &\ sqrt {3}\ frac {N_ {Y} {N_ {N_ {N_ {N}\ Delta}}\ subrayado {V} e^ {j\ frac {\ pi} {6}}
\\ subrayado {V} _ {b Y} = &\ frac {N_ {Y}} {N_ {\ Delta}}\ subrayado {V}\ izquierda (e^ {-j\ frac {2\ pi} {3}} -e^ {j\ frac {2\ pi} {3}}\ derecha) = &\ sqrt {3}\ frac {N_ {Y}} {N_ {\ Delta}}\ subrayado {V} e^ {-j\ frac {\ pi} {2}}\
\ subrayado {V} _ _ {c Y} = &\ frac {N_ {Y}} {N_ {\ Delta}}\ subrayado {V}\ izquierda (e^ {j\ frac {2\ pi} {3}} -1\ derecha) = &\ sqrt {3}\ frac {N_ {Y}} {N_ {\ Delta}}\ subrayado {V} e^ {j\ frac {5\ pi} { 6}}
\ end {array}\)

Se deben hacer aquí dos observaciones:

• La relación de voltajes (es decir, la relación de línea o línea neutra) es diferente de la relación de vueltas por un factor de\(\ \sqrt{3}\).
• Todos los voltajes\(\ wye\) laterales se desplazan en fase 30 ^o con respecto a los voltajes del lado delta.

Ejemplo

Supongamos que tenemos el siguiente problema que resolver:

Una resistencia balanceada trifásica conectada en corriente está conectada al\(\ \Delta\) lado de un\(\ Y-\Delta\) transformador con una relación de voltaje nominal de

\(\ \frac{v_{\Delta}}{v_{Y}}=N\)

¿Cuál es la impedancia que busca en el lado en forma de onda del transformador, suponiendo que la unidad tenga una fuente balanceada?

La situación se muestra en la Figura 18.

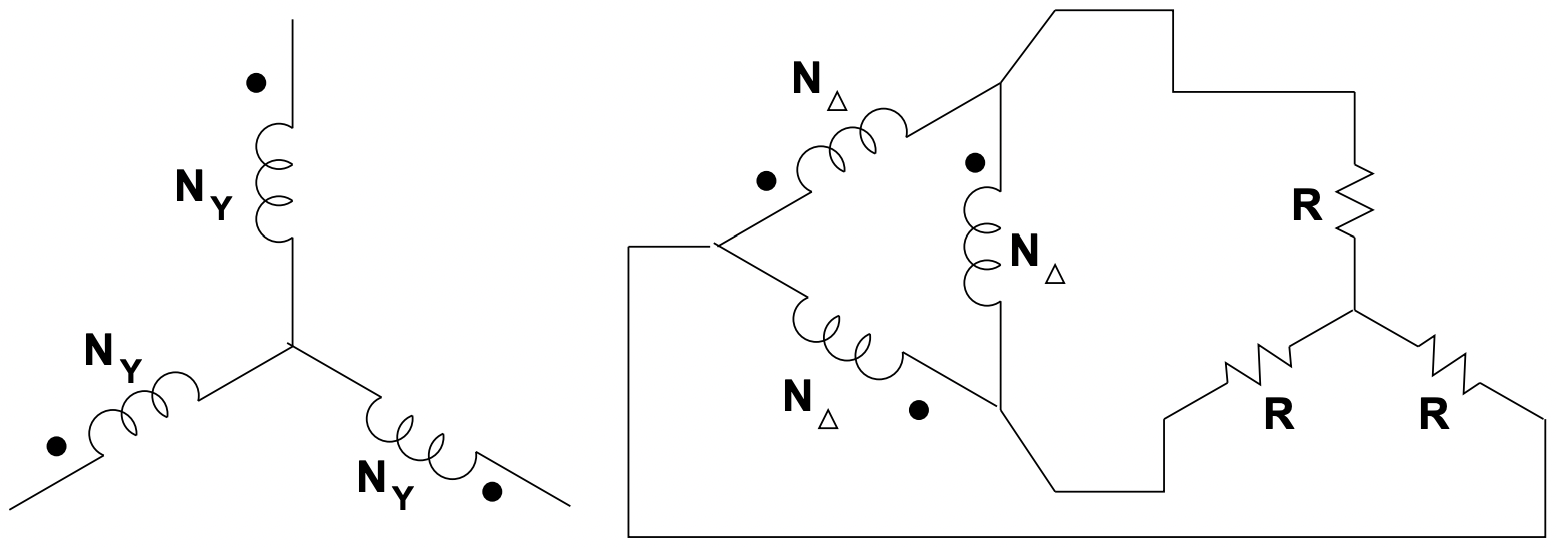Figura 18: Ejemplo

Es importante recordar la relación entre la relación de voltaje y la relación de giros, que es:

\(\ \frac{v_{\Delta}}{v_{Y}}=N=\frac{N_{\Delta}}{\sqrt{3} N_{Y}}\)

de manera que:

\(\ \frac{N_{\delta}}{N_{Y}}=\frac{N}{\sqrt{3}}\)

A continuación, la transformación\(\ Y-\Delta\) equivalente para la carga hace que la imagen se vea como la figura 19

En esta situación, cada devanado secundario del transformador se conecta directamente a través de una de las tres resistencias. Las corrientes en las resistencias vienen dadas por:

\ (\\ begin {alineado}
i_ {1} &=\ frac {v_ {a b\ Delta}} {3 R}\\
i_ {2} &=\ frac {v_ {b c\ Delta}} {3 R}\\
i_ {3} &=\ frac {v_ {c a\ Delta}} {3 R}
\ end {alineado}\)

Las corrientes de línea son:

\ (\\ begin {alineado}
i_ {a\ Delta} =& i_ {1} -i_ {3} =\ frac {v_ {a b\ Delta} -v_ {c a\ Delta}} {3 R} =i_ {1\ Delta} -i_ {3\ Delta}\\
i_ {b\ Delta} =& i_ {2} -i_ {1}\ frac {v_ {b c\ Delta} -v_ {a b\ Delta}} {3 R} =i_ {2\ Delta} -i_ {1\ Delta}\\
i_ {c\ Delta} =& i_ {3} -i_ {2} =\ frac {v_ {c a\ Delta} -v_ {b c\ Delta}} {3 R} =i_ {3\ Delta} -i_ {2\ Delta}
\ final {alineado}\)

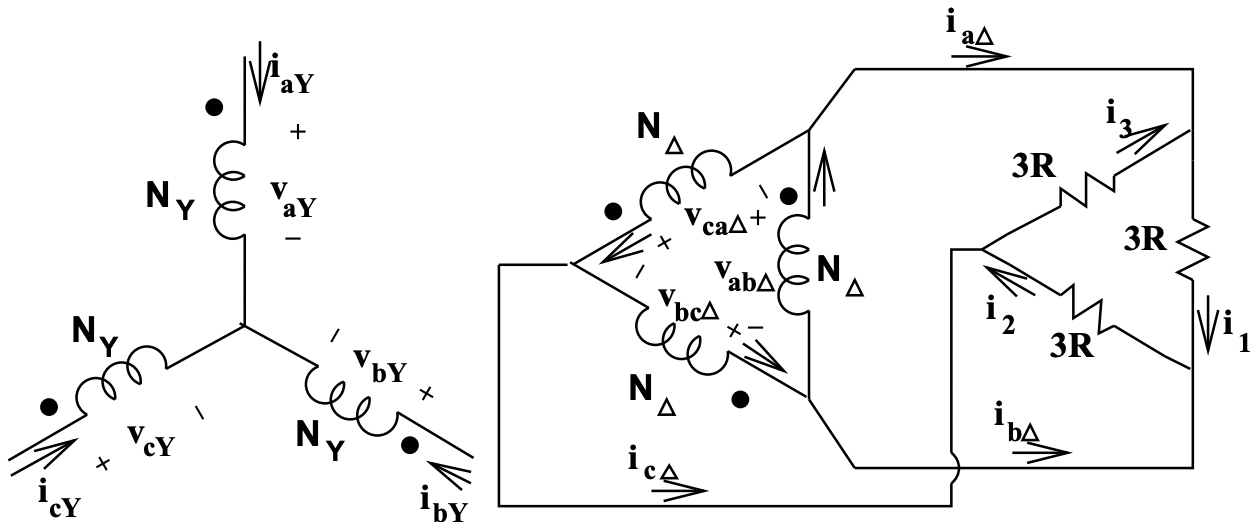Figura 19: Situación equivalente

Resolviendo corrientes en las patas del transformador\(\ \Delta\), restar, por ejemplo, la segunda expresión de la primera:

\(\ 2 i_{1 \Delta}-i_{2 \Delta}-i_{3 \Delta}=\frac{2 v_{a b \Delta}-v_{b c \Delta}-v_{c a \Delta}}{3 R}\)

Ahora, aprovechando que el sistema está equilibrado:

\ (\\ begin {array} {r}
i_ {1\ Delta} +i_ {2\ Delta} +i_ {3\ Delta} =0\
v_ {a b\ Delta} +v_ {b c\ Delta} +v_ {c a\ Delta} =0
\ end {array}\)

para encontrar:

\ (\\ begin {array} {l}
i_ {1\ Delta} =\ frac {v_ {a b\ Delta}} {3 R}\
i_ {2\ Delta} =\ frac {v_ {b c\ Delta}} {3 R}\
i_ {3\ Delta} =\ frac {v_ {c a\ Delta}} {3 R}
\ end {array}\)

Por último, las relaciones transformadoras ideales dan:

\ (\\ comenzar {array} {ll}
v_ {a b\ Delta} =\ frac {N_ {\ Delta}} {N_ {Y}} v_ {a Y} & i_ {a Y} =\ frac {N_ {\ Delta}} {N_ {Y}} i_ {1\ Delta}\
v_ {b c\ Delta} =\ frac {N_ {\ Delta}} {N_ {Y}} v_ {b Y} & i_ {b Y} =\ frac {N_ {\ Delta}} {N_ {Y}} i_ {2\ Delta}\\
v_ {c a\ Delta} =\ frac {N_ {\ Delta}} {N_ {Y} v _ {c Y} & i_ {c Y} =\ frac {N_ {\ Delta}} {N_ {Y}} i_ {3\ Delta}
\ end {array}\)

de manera que:

\ (\\ comenzar {alineado}
i_ {a Y} &=\ izquierda (\ frac {N_ {\ Delta}} {N_ {Y}}\ derecha) ^ {2}\ frac {1} {3 R} v_ {a Y}\\
i_ {b Y} &=\ izquierda (\ frac {N_ {\ Delta}} {N_ {Y}}\ derecha) ^ {2}\ frac {1} {3 R} v_ {b Y}\\
i_ {c Y} &=\ izquierda (\ frac {N_ {\ Delta}} {N_ {Y}}\ derecha) ^ {2}\ frac {1} {3 R} v_ {c Y}
\ end {alineado}\)

La resistencia aparente (es decir, aparente si se conectara\(\ wye\)) en los\(\ wye\) terminales del transformador es:

\(\ R_{e q}=3 R\left(\frac{N_{Y}}{N_{\Delta}}\right)^{2}\)

Expresado en términos de relación de voltaje, esto es:

\(\ R_{e q}=3 R\left(\frac{N}{\sqrt{3}}\right)^{2}=R\left(\frac{v_{Y}}{v_{\Delta}}\right)^{2}\)

Es importante señalar que esta solución tomó el largo camino alrededor. Tomadas de manera consistente (uniformemente en línea neutra o uniformemente sobre una base de línea lineal), las impedancias se transforman a través de transformadores por el cuadrado de la relación de voltaje, independientemente de la conexión que se use.