4.6: Fallos desequilibrados

Una aplicación muy común de componentes simétricos es en el cálculo de las corrientes que surgen de cortocircuitos no blancados. Para los sistemas trifásicos, las posibles fallas desequilibradas son:

1. Una sola línea de tierra,
2. Doble línea de tierra,
3. Línea de línea.

Estos se consideran por separado.

Fallo único de línea a tierra

La situación es como se muestra en la Figura 10

El sistema en este caso consiste en redes conectadas a la línea en la que se produce la falla. El punto de falla en sí consiste en un conjunto de terminales (que podríamos llamar “a, b, c”). Los conjuntos de fallas,

Figura 9: Red de secuencia cero: conexión Wye-Delta, sin conexión a tierra o Delta-Delta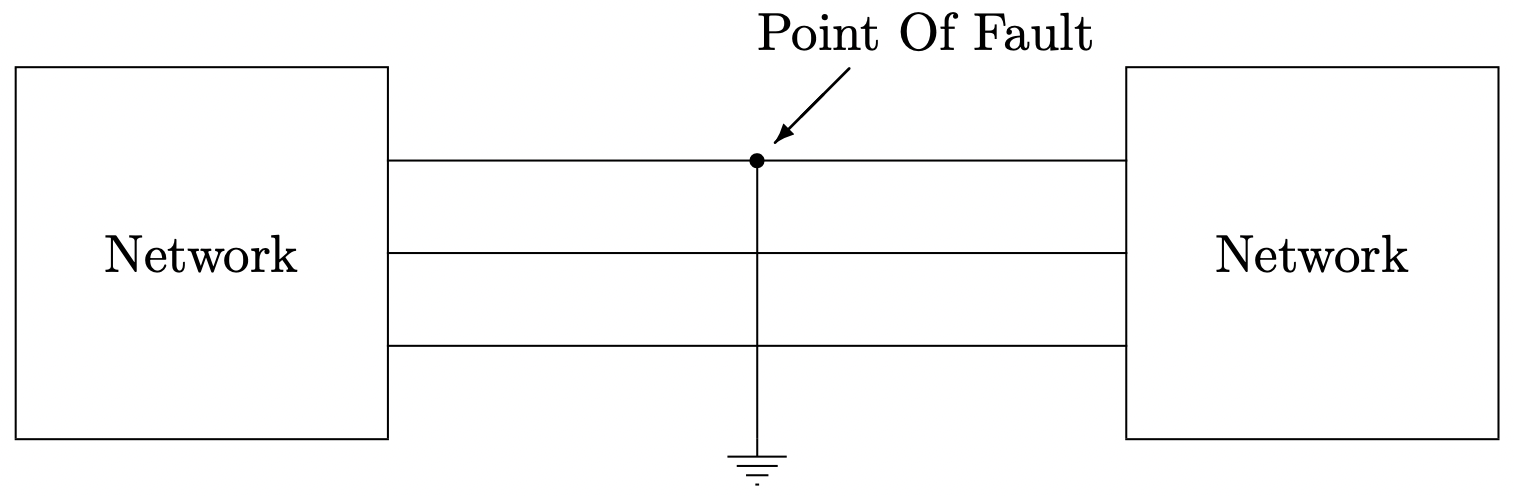

Figura 10: Imagen esquemática de una sola falla de línea a tierra

en este punto del sistema:

\ (\\ comenzar {alineado}
\ subrayado {V} _ {a} &=0\\
\ subrayado {I} _ {b} &=0\\
\ subrayado {I} _ _ {c} &=0
\ end {alineado}\)

Ahora: usando la inversa de la transformación de componentes simétricos, vemos que:

\[\ \underline{V}_{1}+\underline{V}_{2}+\underline{V}_{0}=0\label{58} \]

Y usando la transformación misma:

\[\ \underline{I}_{1}=\underline{I}_{2}=\underline{I}_{0}=\frac{1}{3} \underline{I}_{a}\label{59} \]

Juntas, estas dos expresiones describen la conexión de red de secuencia mostrada en la Figura 11. Esta conexión tiene las tres redes de secuencia conectadas en serie.

Doble falla de línea a tierra

Si la falla involucra las fases b, c y tierra, la relación “terminal” en el punto de la falla es:

\ (\\ begin {array} {l}
\ subrayado {V} _ {b} =0\\
\ subrayado {V} _ {c} =0\\
\ subrayado {I} _ {a} =0
\ end {array}\)

Luego, usando la transformación de secuencia:

\(\ \underline{V}_{1}=\underline{V}_{2}=\underline{V}_{0}=\frac{1}{3} \underline{V}_{a}\)

Combinando la transformación inversa:

\(\ \underline{I}_{a}=\underline{I}_{1}+\underline{I}_{2}+\underline{I}_{0}=0\)

Estos describen una situación en la que las tres redes de secuencia están conectadas en paralelo, como se muestra en la Figura 12.

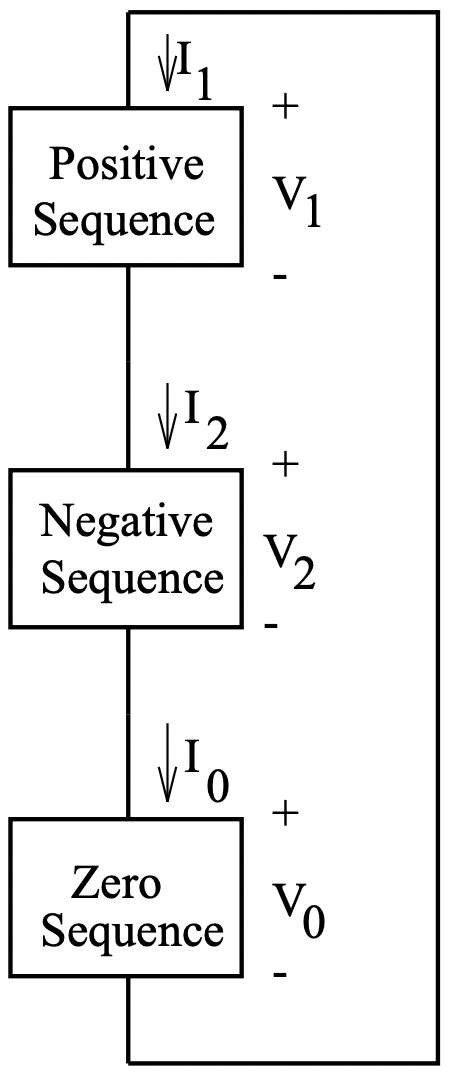Figura 11: Conexión secuencial para una falla de línea única a tierra

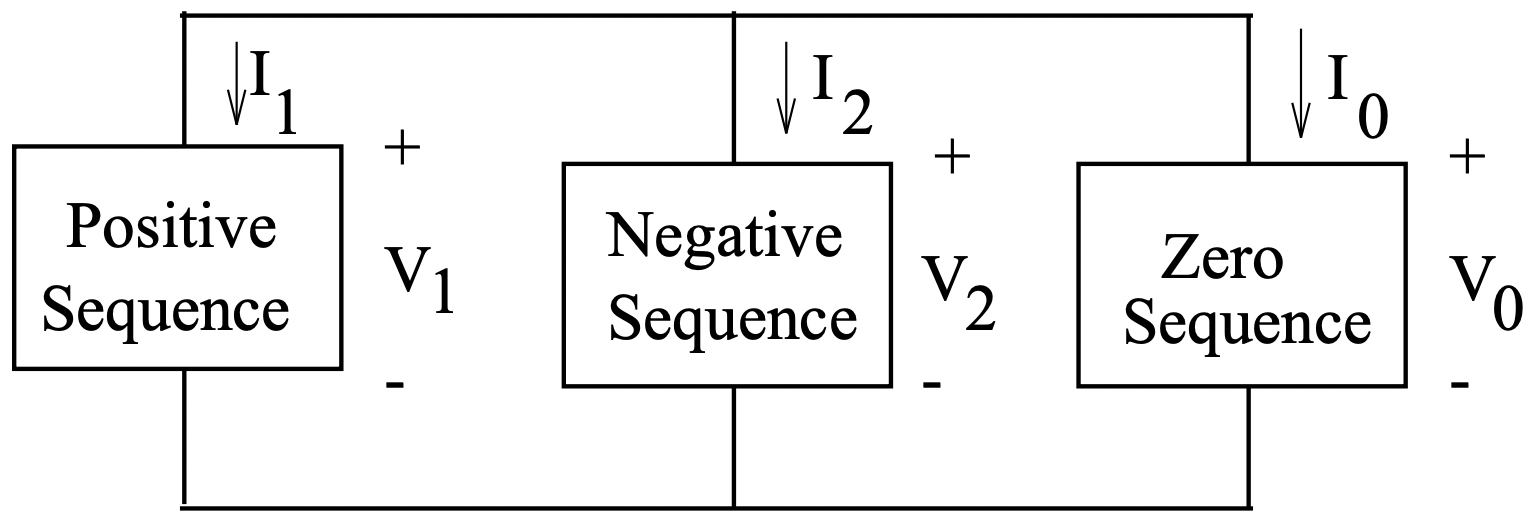Figura 12: Conexión de secuencia para una falla de doble línea a tierra

Fallo de línea de línea

Si las fases b y c se cortocircuitan juntas pero no se ponen a tierra,

\ (\\ comenzar {alineado}
\ subrayado {V} _ {b} &=\ subrayado {V} _ _ {c}\
\ subrayado {I} _ {b} &=-\ subrayado {I} _ _ {c}\
\ subrayado {I} _ {a} &=0
\ end {alineado}\)

Expresando estos en términos de los componentes simétricos:

\ (\\ comenzar {alineado}
\ subrayado {V} _ {1} &=\ subrayado {V} _ _ {2}\
&=\ frac {1} {3}\ izquierda (\ subrayado {a} +\ subrayado {a} ^ {2}\ derecha)\ subrayado {V} _ _ {b}\
\ subrayado {I} _ _ {0} &=\ subrayado I} _ {a} +\ subrayado {I} _ {b} +\ subrayado {I} _ _ {c}\\
&=0\\
\ subrayado {I} _ {a} &=\ subrayado {I} _ {1} +\ subrayado {I} _ {2}\\
&=0
\ end {alineado}\)

Estas expresiones describen una conexión paralela de las redes de secuencia positiva y negativa, como se muestra en la Figura 13.

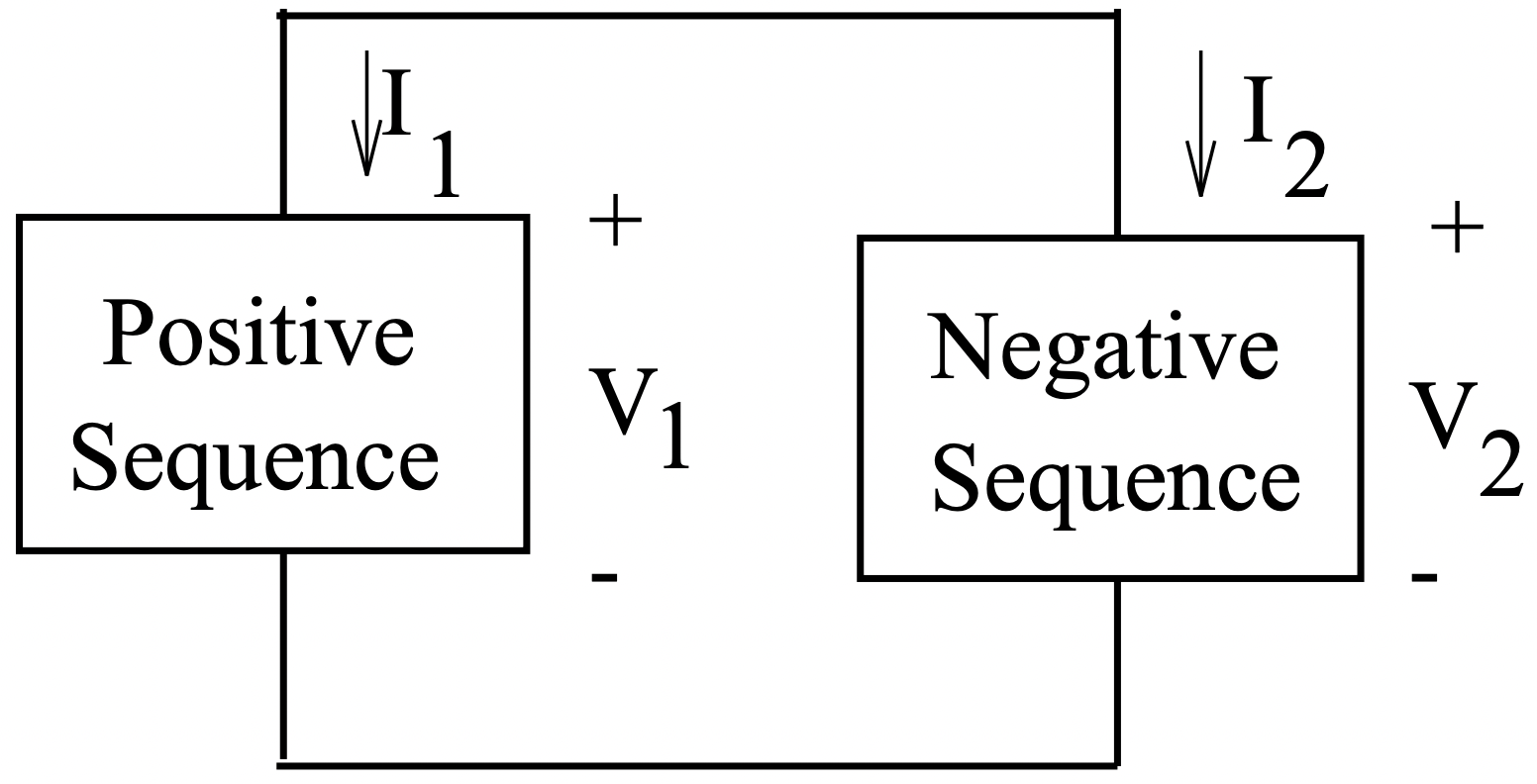Figura 13: Conexión de secuencia para un fallo de línea a línea

Ejemplo de Cálculos de Fallos

En este ejemplo, el objetivo es determinar la corriente máxima a través del disyuntor B debido a una falla en la ubicación mostrada en la Figura 14. Se deben considerar los tres tipos de falla desequilibrada, así como la falla balanceada. Este es el tipo de cálculo que se tiene que hacer cada vez que se instala o modifica una línea, para que la reinstalación de protección se pueda configurar correctamente.

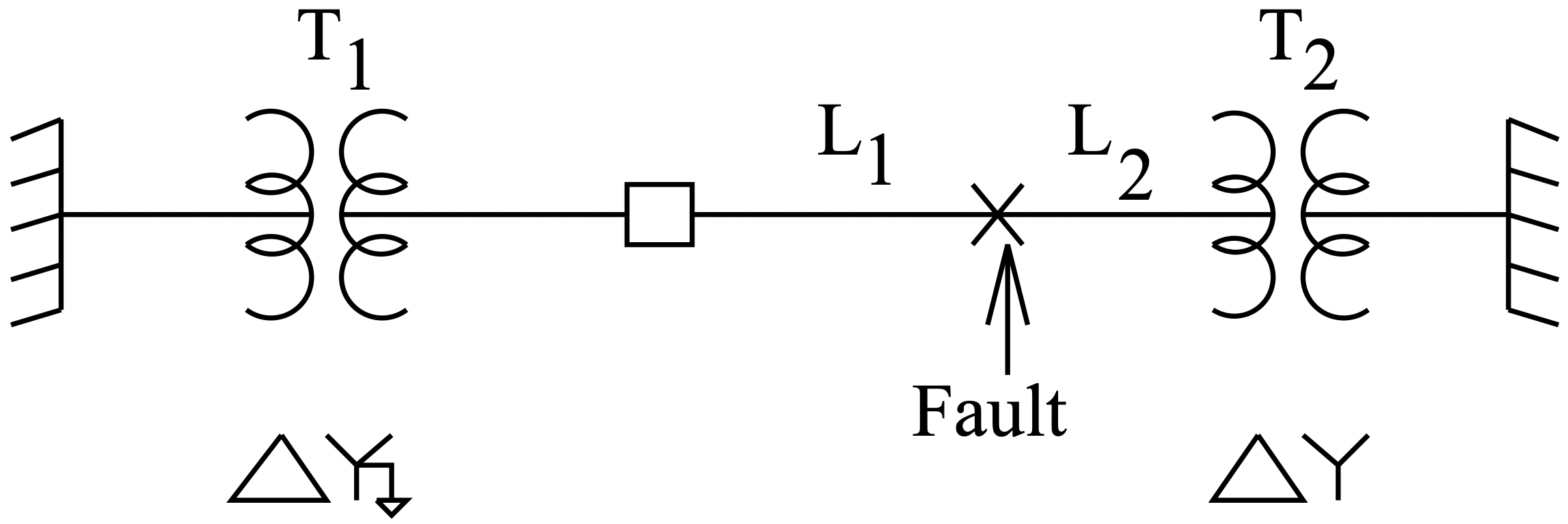Figura 14: Diagrama unifilar por error de ejemplo

Los parámetros del sistema son:

Voltaje base del sistema	138 kV
Potencia Base del Sistema	100 MVA
Reactancia\(\ T_{1}\) de fuga del transformador	.1 por unidad
Reactancia\(\ T_{2}\) de fuga del transformador	.1 por unidad
Reactancia de secuencia\(\ L_{1}\) positiva y negativa de línea	j.05 por unidad
Línea de impedancia de secuencia\(\ L_{1}\) cero	j.1 por unidad
Reactancia de secuencia\(\ L_{2}\) positiva y negativa de línea	j.02 por unidad
Línea de impedancia de secuencia\(\ L_{2}\) cero	j.1 por unidad

Los símbolos similares a cercas en cada extremo de la figura representan “buses infinitos”, o fuentes de voltaje de secuencia positiva.

El primer paso en esto es encontrar las redes de secuencia. Estos se muestran en la Figura 15. Tenga en cuenta que son exactamente como lo que esperaríamos haber dibujado para redes monofásicas equivalentes. Solo la red de secuencia positiva tiene fuentes, porque el bus infinito suministra solo voltaje de secuencia positiva. La red de secuencia cero está abierta en el lado derecho debido a la conexión del transformador deltawye allí.

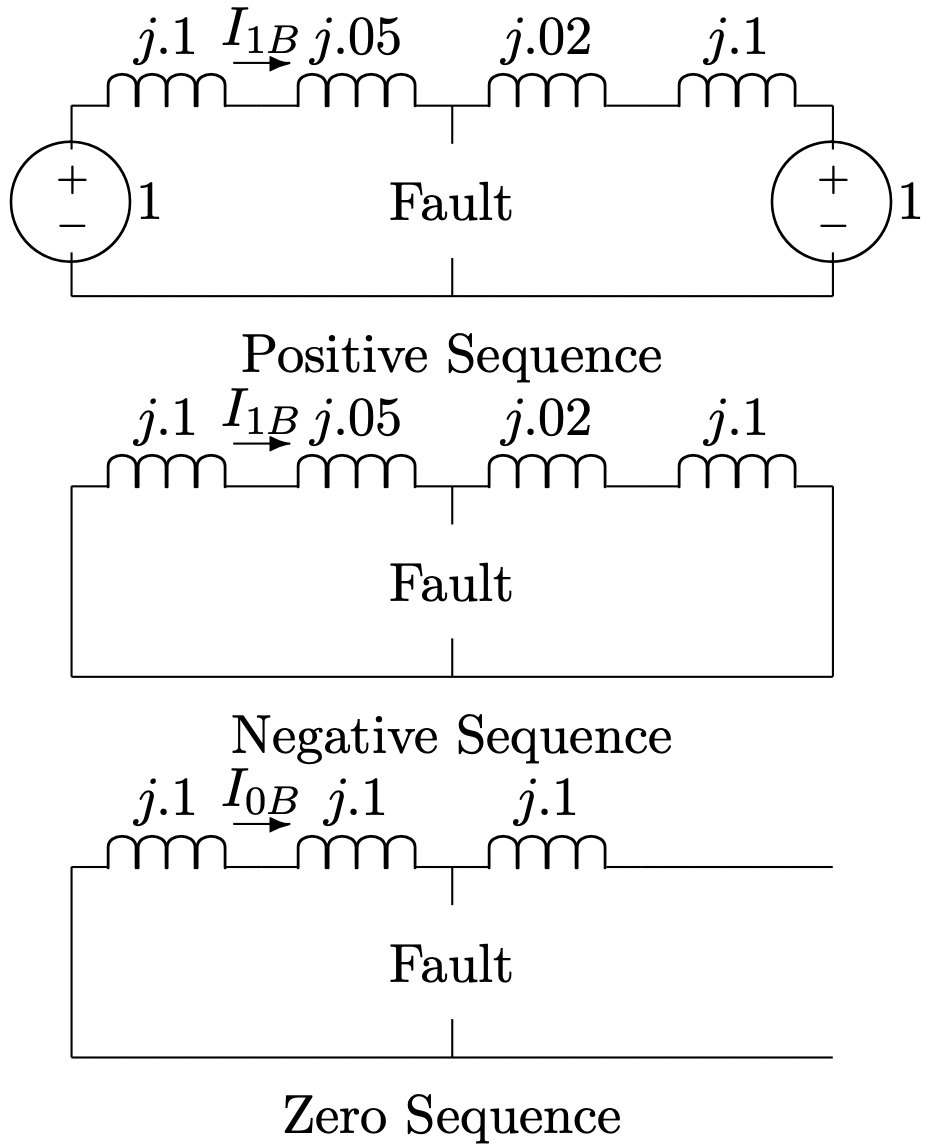Figura 15: Redes de Secuencia

Fallo simétrico

Para una falla simétrica (trifásica), solo está involucrada la red de secuencia positiva. La falla corta la red en su posición, de manera que la corriente es:

\(\ \underline{i}_{1}=\frac{1}{j .15}=-j 6.67 \text { per }-\text { unit }\)

Fallo de tierra de línea única

Para esta situación, las tres redes están en serie y la situación es como se muestra en la Figura 16

La corriente\(\ \underline{i}\) mostrada en la Figura 16 es una corriente total, y viene dada por:

\(\ \underline{i}=\frac{1}{2 \times(j .15 \| j .12)+j .2}=-j 3.0\)

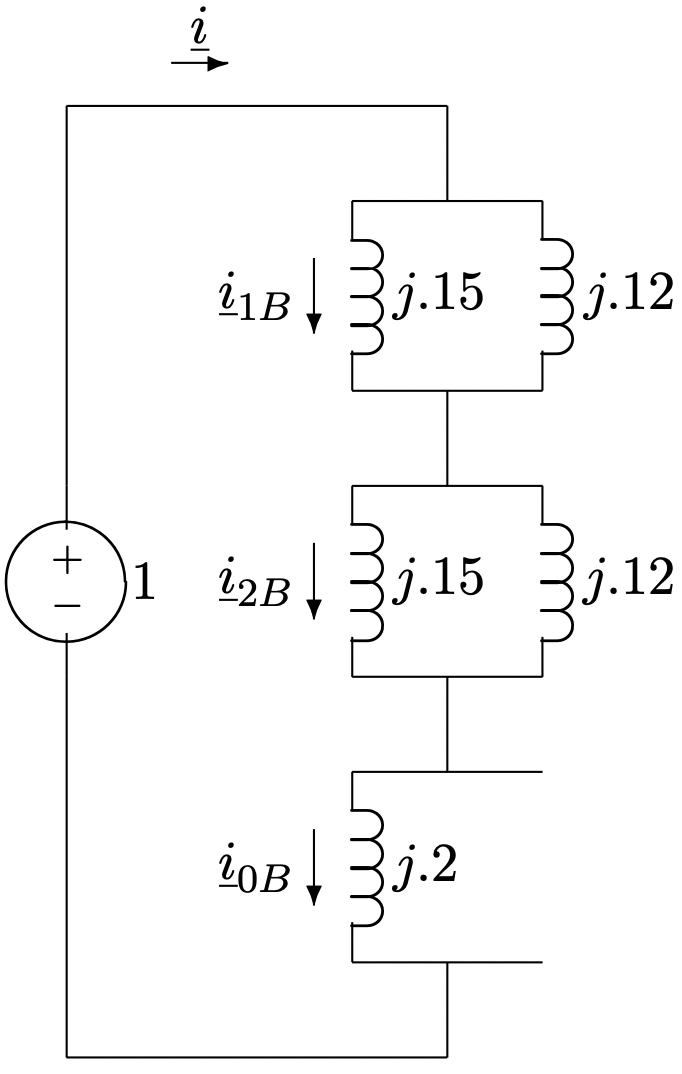Figura 16: Red terminada para falla de tierra de línea única

Entonces las corrientes de secuencia en el interruptor son:

\ (\\ comenzar {alineado}
\ subrayado {i} _ {1 B} &=\ subrayado {i} _ {2 B}\\
&=\ subrayado {i}\ veces\ frac {j .12} {j .12+j .15}\\
&=-j 1.33\\
\ subrayado {i} _ _ {0 B} &=\ subrayado {i}\
&=-j 3.0
\ fin {alineado}\)

Las corrientes de fase se reconstruyen usando:

\ (\\ comenzar {alineado}
\ subrayado {i} _ {a} &=\ subrayado {i} _ {1 B} +\ subrayado {i} _ {2 B} +\ subrayado {i} _ {0 B}\
\ subrayado {i} _ {b} &=\ subrayado {a} ^ {2}\ subrayado {i} _ {1 B} +\ subrayado {ai} _ {2 B} +\ subrayado {i} _ {0 B}\\
\ subrayado {i} _ {c} &=\ subrayado {ai} _ {1 B} +\ subrayado { a} ^ {2}\ subrayado {i} _ {2 B} +\ subrayado {i} _ {0 B}
\ final {alineado}\)

Estos son:

\ (\\ begin {alineado}
i_ {a} &=-j 5.66 & &\ text {por unidad}\\
\ subrayado {i} _ {b} &=-j 1.67 & &\ text {por unidad}\
\ subrayado {i} _ {c} &=-j 1.67 & &\ text {por unidad}
\ end {alineado}\)

Fallo de doble línea a tierra

Para la falla de doble línea a tierra, las redes están en paralelo, como se muestra en la Figura 17.

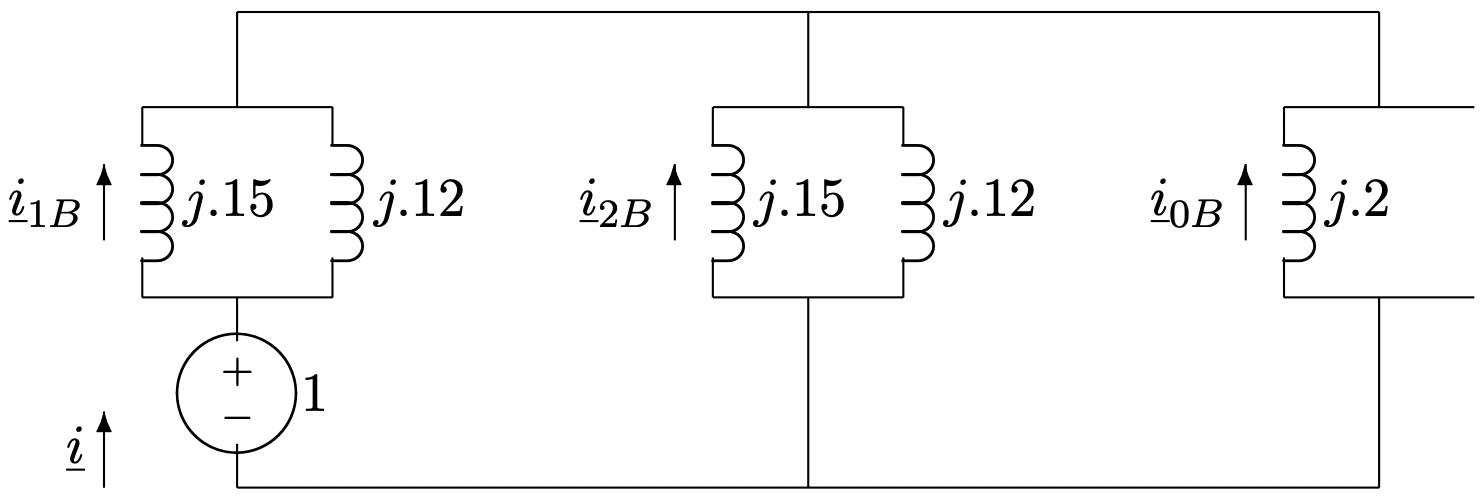Figura 17: Red terminada para falla de tierra de línea doble

Para comenzar, encuentre la fuente actual\(\ \underline{i}\):

\ (\\ comenzar {alineado}
\ subrayado {i} &=\ frac {1} {j (.15||\ cdot 12) +j (.15|| .12|| .2)}\\
&=-j 8.57
\ end {alineado}\)

Entonces las corrientes de secuencia en el interruptor son:

\ (\\ comenzar {alineado}
\ subrayado {i} _ {1 B} &=\ subrayado {i}\ veces\ frac {j .12} {j .12+j .15}\\
&=-j 3.81\\
\ subrayado {i} _ {2 B} &=-\ subrayado {i}\ veces\ frac {j .12\ | j .2} {j .12\ | j .2+j .15}\\
&=j 2.86\\
\ subrayado {i} _ {0 B} &=\ subrayado {i}\ veces\ frac {j .12\ | j .15} {j .2+j .12\ | j .15}\\
&=j 2.14
\ end {alineado}\)

Las corrientes de fase reconstruidas son:

\ (\\ comenzar {alineado}
\ subrayado {i} _ {a} &=j 1.19\\
\ subrayado {i} _ {b} &=\ subrayado {i} _ {0 B} -\ frac {1} {2}\ izquierda (\ subrayado {i} _ {1 B} +\ subrayado {i} _ {2 B}\ derecha) -\ frac {\ sql rt {3}} {2} j\ izquierda (\ subrayado {i} _ {1 B} -\ subrayado {i} _ {2 B}\ derecha)\\
&=j 2.67-5.87\\
\ subrayado {i} _ {c} &=\ subrayado {i} _ {0 B} -\ frac {1} {2}\ izquierda (\ subrayado {i} _ {1 B} +\ subrayado {i} _ {2 B}\ derecha) +\ frac {\ sqrt {3}} {2} j\ izquierda (\ subrayado {i} _ _ {1 B} -\ subrayado {i} _ {2 B}\ derecha)\\
&=j 2.67+5.87\\
|\ subrayado {i} _ {a}\ mid &=1.19\ quad\ text {por unidad}\\
\ izquierda|\ subrayado {i} _ {b}\ derecha| &=6.43\ quad\ texto {por unidad}\\
\ izquierda|i_ {c}\ derecha| &=6.43\ quad\ texto {por unidad}
\ end {alineado}\)

Fallo de línea de línea

La situación es aún más fácil aquí, como se muestra en la Figura 18

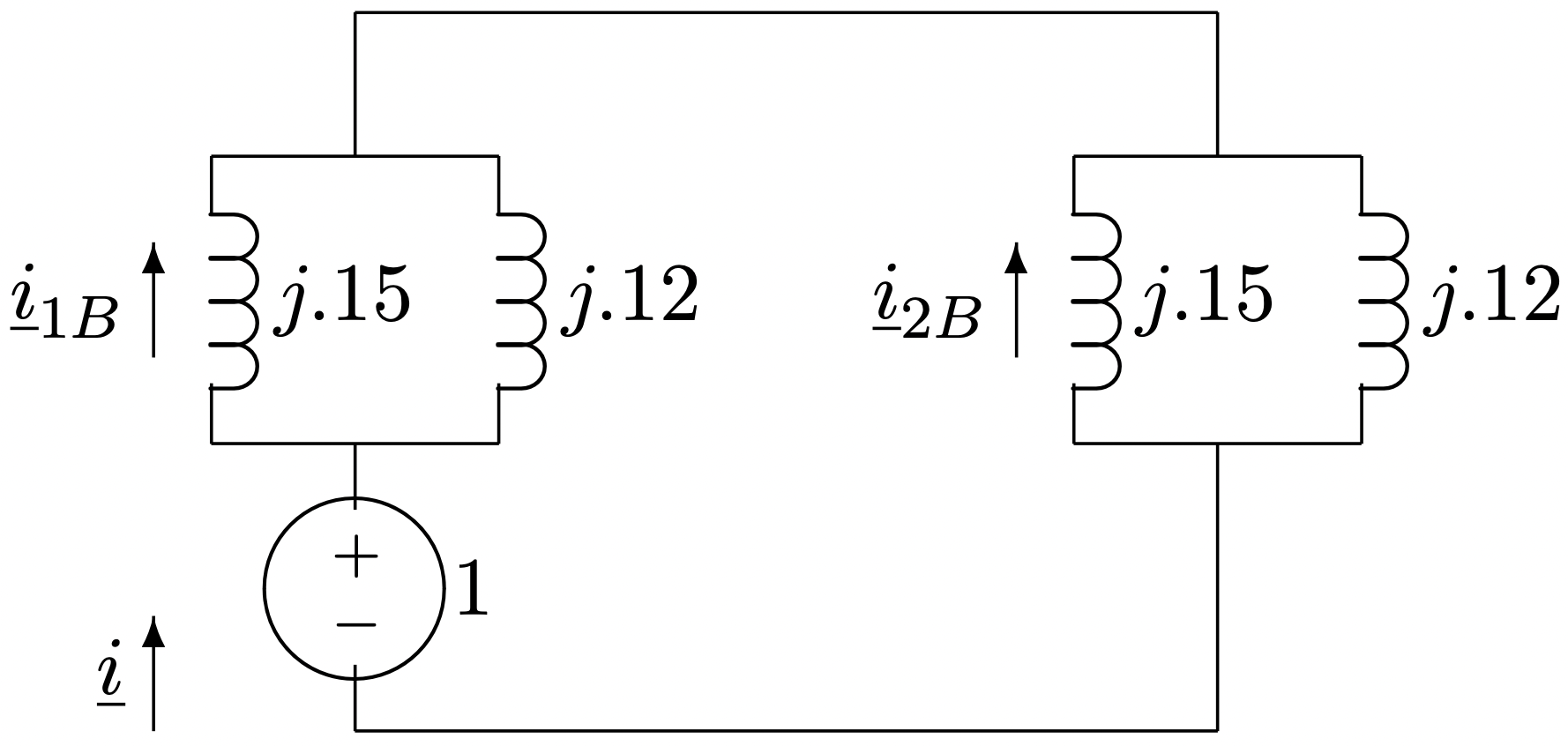Figura 18: Red completada para falla de línea de línea

La corriente de origen\(\ \underline{i}\) es:

\ (\\ comenzar {alineado}
\ subrayado {i} &=\ frac {1} {2\ veces j (.15\ | .12)}\\
&=-j 7.50
\ end {alineado}\)

y luego:

\ (\\ comenzar {alineado}
\ subrayado {i} _ {1 B} &=-\ subrayado {i} _ {2 B}\\
&=i\ frac {j .12} {j .12+j .15}\\
&=-j 3.33
\ end {alineado}\)

Las corrientes de fase son:

\ (\\ comenzar {alineado}
\ subrayado {i} _ {a} &=0\\
\ subrayado {i} _ {b} &=-\ frac {1} {2}\ izquierda (\ subrayado {i} _ {1 B} +\ subrayado {i} _ _ {2 B}\ derecha) -j\ frac {\ sqrt {3}} {2}\ izquierda (\ subrayado {i} _ {1 B} -\ subrayado {i} _ _ {2 B}\ derecha)\\\ izquierda|
\ subrayado {i} _ _ {b}\ derecha| &=5.77\ quad\ text { por unidad}\\
\ izquierda|i_ {c}\ derecha| &=5.77\ quad\ texto {por unidad}
\ end {alineado}\)

Conversión a Amperios

La corriente base es:

\(\ I_{B}=\frac{P_{B}}{\sqrt{3} V_{B l-l}}=418.4 A\)

Entonces las amplitudes de corriente son, en Amperios, RMS:

	Fase A	Fase B	Fase C
Fallo trifásico	2791	2791	2791
Línea Única a tierra,\(\ \phi_{a}\)	2368	699	699
Doble línea de tierra,\(\ \phi_{b}, \phi_{c}\)	498	2690	2690
Línea de línea,\(\ \phi_{b}, \phi_{c}\)	0	2414	2414