6.2: Circuitos Magnéticos

Resulta que los circuitos magnéticos son muy similares y se rigen por leyes que no son en absoluto diferentes a las de los circuitos eléctricos, con sólo una diferencia menor.

Conservación del Flujo: Ley de Gauss

Para comenzar, la ley de Gauss es:

\(\ \oiint \vec{B} \cdot d \vec{a}=0\)

Esto refleja esa noción de que no hay fuentes de flujo: se trata de una cantidad verdaderamente sinusoidal. Ni comienza ni termina sino que simplemente va en círculos.

Si observamos una fracción de la superficie alrededor de un nodo y lo llamamos superficie k, el flujo a través de esa superficie es:

\(\ \Phi_{k}=\iint \ _{A_{k}} \vec{B} \cdot d \vec{a}\)

Si tomamos la suma de todos los flujos parciales a través de una superficie que rodea una nota llegamos al análogo de KCL:

\(\ \sum_{k} \Phi_{k}=0\)

MMF: Ley de Ampere

La Ley de Ampere se establece simplemente como:

\(\ \oint \vec{H} \cdot d \ell=\iint \vec{J} \cdot d \vec{a}\)

La integral de densidad de corriente\(\ \vec{J}\) es la corriente, cuantificada en el sistema SI como Amperios. Como generalmente se lleva en cables que podrían numerar, digamos,\(\ N\), a menudo se cuantifica como:

\(\ \iint \vec{J} \cdot d \vec{a}=N I\)

Para ello a menudo usaremos el término Fuerza MagnetoMotiva o MMF, que obtiene el símbolo\(\ F\). Si usamos ese símbolo para denotar la integral del campo magnético sobre un elemento de circuito magnético:

\(\ F_{k}=\int_{a_{k}}^{b_{k}} \vec{H} \cdot d \vec{\ell}\)

Entonces, si tomamos suficientes de estas subintegrales para cubrir el bucle alrededor de un grupo de elementos, tenemos

\(\ \sum_{k} F_{k}=N I\)

Tenga en cuenta que esto no es exactamente lo mismo que KVL, ya que tiene un término fuente a la derecha.

Elemento de circuito magnético: Analogía a la ley de Ohm

Los circuitos magnéticos tienen un equivalente a la resistencia. Es la relación de MMF a flujo y tiene el símbolo\(\ \mathcal{R}\). I comparación directa con la derivación de resistencia, se muestra un elemento de circuito magnético en la Figura 2.

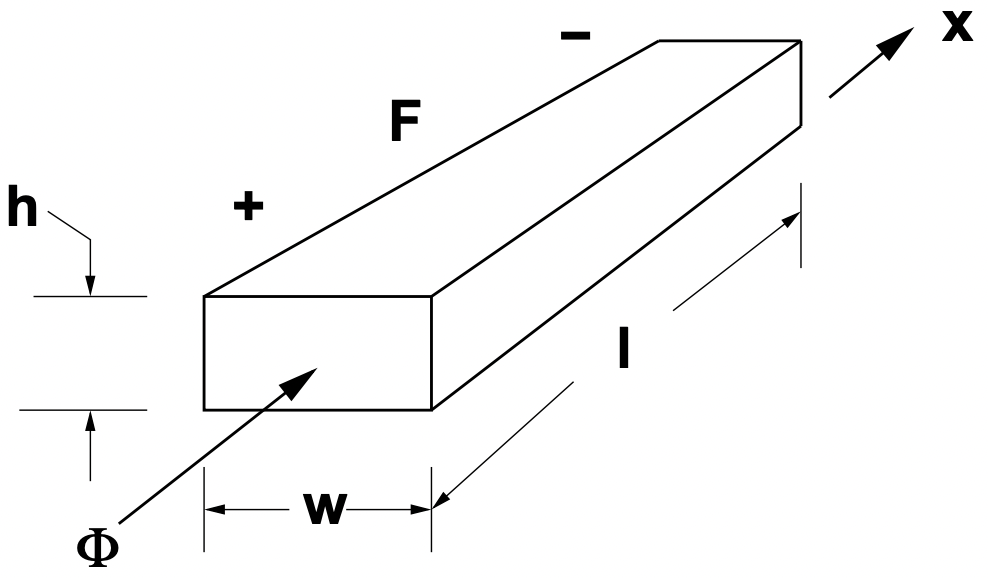Figura 2: Elemento de circuito magnético

Supongamos que el material de este elemento tiene permeabilidad\(\ \mu>\mu_{0}\), por lo que tiene una relación constitutiva:

\(\ B_{x}=\mu H_{x}\)

Si la densidad de flujo en el material es uniforme, el flujo total a través del elemento es:

\(\ \Phi=h w B_{x}=h w \mu H_{x}\)

Y el MMF es simplemente la integral del campo magnético H de un extremo a otro: nuevamente asumimos uniformidad para que:

\(\ F=\ell H_{x}\)

La renuencia de este elemento es entonces:

\(\ \mathcal{R}=\frac{F}{\Phi}=\frac{\ell}{h w \mu}\)

Brechas Magnéticas

En realidad, los circuitos magnéticos tienden a estar formados por elementos muy permeables (piezas de hierro) y brechas de aire relativamente pequeñas. Un boceto de tal hueco se muestra en la Figura 3.

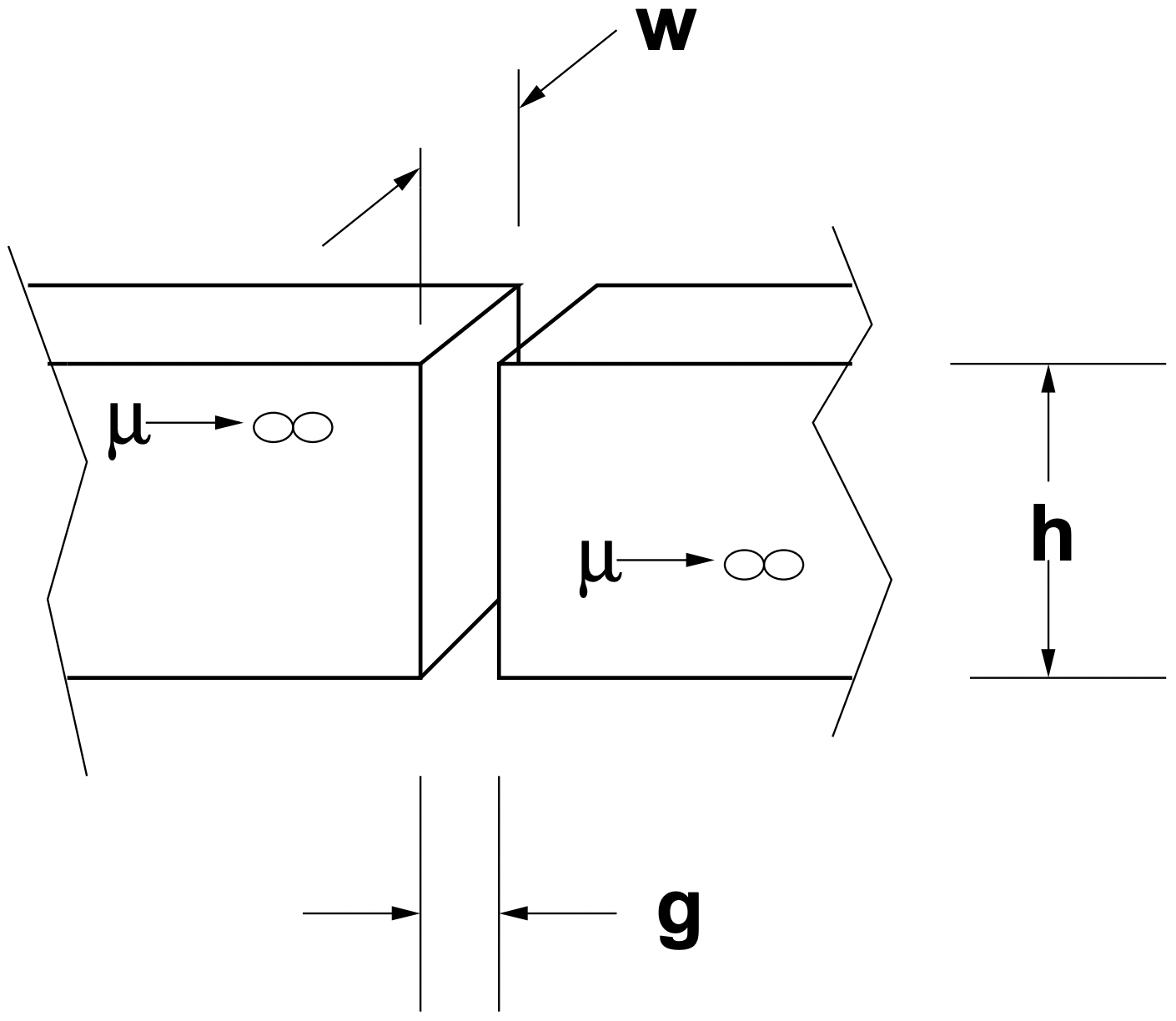Figura 3: Brecha entre elementos magnéticos

Por lo general, es permisible suponer que los elementos de hierro tienen una permeabilidad muy alta\(\ (\mu \rightarrow \infty)\), por lo que hay una caída insignificante de MMF. En este sentido los elementos de hierro sirven en el mismo papel que el alambre de cobre o aluminio en los circuitos eléctricos. La brecha, por otro lado, tiene renuencia:

\(\ \mathcal{R}_{g}=\frac{g}{h w \mu_{0}}\)

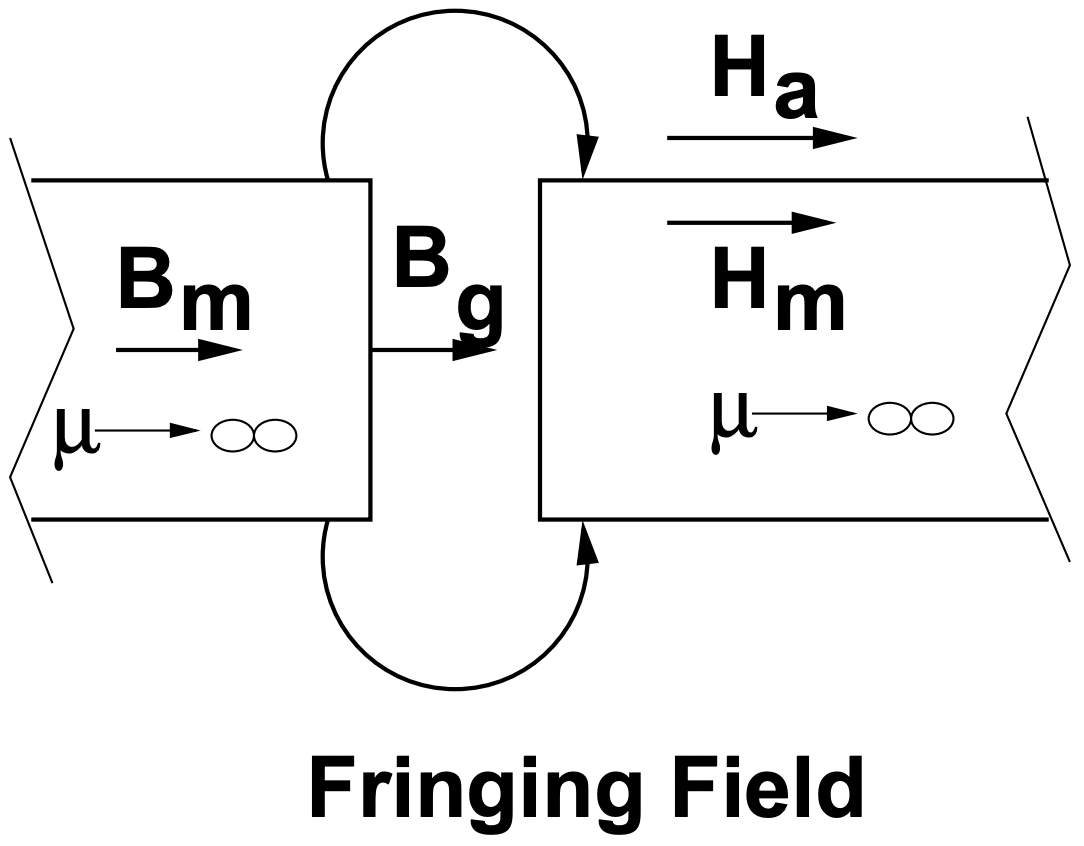Figura 4: Detalles de la brecha

Condiciones de Límite

En la Figura 4 se muestra la sección transversal de un hueco. Se supone que los elementos mostrados tienen cierta profundidad en el papel que es mayor que el ancho del hueco\(\ g\). Si la permeabilidad de los elementos a la derecha y a la izquierda es muy alta, decimos que el flujo magnético se limita en gran medida a esos elementos. Tenga en cuenta que la condición límite asociada a la Ley de Ampere dicta que la intensidad del campo magnético\(\ H_{a}\) en el aire adyacente al material permeable y paralela a la superficie debe ser igual a la intensidad del campo magnético\(\ H_{m}\) justo dentro del material magnético y paralela a la superficie . Si el material es muy altamente permeable\(\ (\mu \rightarrow \infty)\), ese campo magnético debe ser casi cero:\(\ H_{a}=H_{m} \rightarrow 0\). Esto significa que el campo magnético debe ser perpendicular a la superficie de material muy altamente permeable. Este es el caso en la propia brecha, donde:

\(\ B_{g}=B_{m}\)

Debemos señalar, sin embargo, que habrá campos 'marginales' en la región cerca de la brecha, de manera que nuestra expresión por la renuencia de la brecha no será del todo correcta. La precisión de la expresión que ignora la franja es mejor para brechas realmente pequeñas y generalmente sobreestima la renuencia.