8.4: Impedancia superficial de conductores uniformes

El objetivo de esta sección es describir el cálculo de la impedancia superficial que presenta una capa de material conductor. Aquí se consideran dos problemas. El primero considera una capa de material lineal respaldada por una superficie infinitamente permeable. Esta es aproximadamente la situación que presentan, por ejemplo, los imanes permanentes montados en superficie y probablemente sea una aproximación decente al mecanismo de conducción que sería responsable de la pérdida por armónicos asíncronos en estas máquinas. También es apropiado para su uso en la estimación de pérdidas en máquinas de inducción de rotor sólido y en los polos de turbogeneradores. El segundo problema, que no trabajamos aquí sino que simplemente presentamos la solución previamente trabajada, se refiere a saturar material ferromagnético.

Caso Lineal

La situación y el sistema de coordenadas se muestran en la Figura 7. La capa conductora es de espesores\(\ T\) y tiene conductividad\(\ \sigma\) y permeabilidad\(\ \mu_{0}\). Para mantener las expresiones matemáticas dentro de límites, asumimos geometría rectilínea. Esta suposición presentará errores que son pequeños en la medida en que la curvatura del problema es pequeña en comparación con los números de onda encontrados. Presumimos que la situación está excitada, como lo sería en una máquina eléctrica, por una hoja actual de la forma\(\ K_{z}=\operatorname{Re}\left\{\underline{K} e^{j(\omega t-k x)}\right\}\).

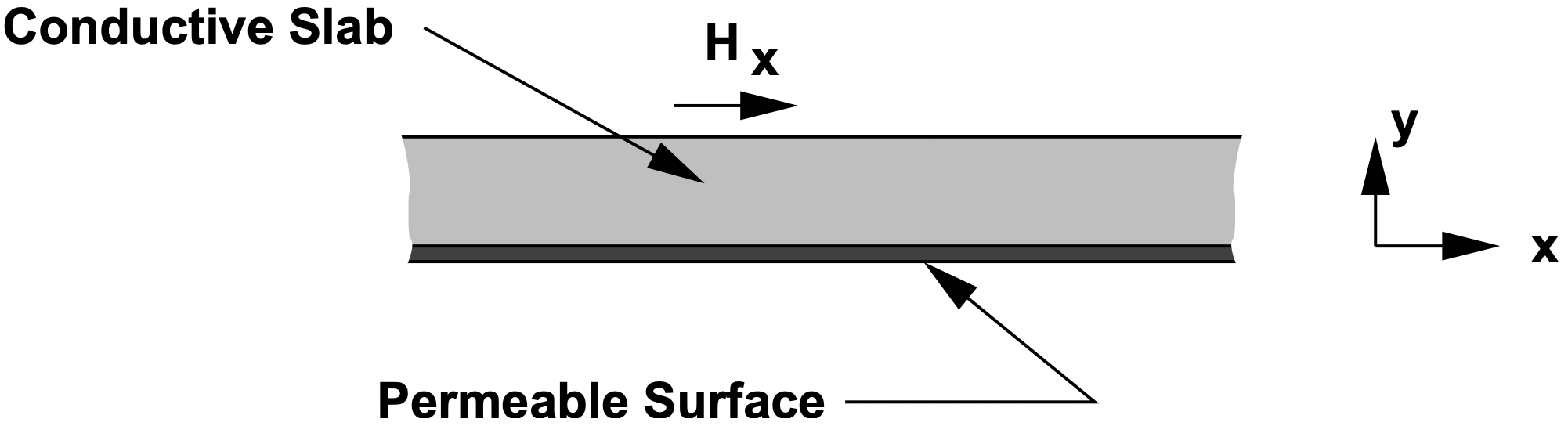Figura 7: Vista axial del problema del campo magnético

En el material conductor, debemos satisfacer la ecuación de difusión:

\(\ \nabla^{2} \bar{H}=\mu_{0} \sigma \frac{\partial \bar{H}}{\partial t}\)

En vista de la condición de contorno en la superficie posterior del material, tomando ese punto para ser\(\ y=0\), una solución general para el campo magnético en el material es:

\ (\\ comenzar {alineado}
H_ {x} &=\ nombreoperador {Re}\ izquierda\ {A\ sinh\ alfa y e^ {j (\ omega t-k x)}\ derecha\}\
H_ {y} &=\ nombreoperador {Re}\ izquierda\ {j\ frac {k} {\ alfa} A\ cosh\ alfa y e^ {j (\ omega t-k x)}\ derecha\}
\ final {alineado}\)

cuando el coeficiente α satisfaga:

\(\ \alpha^{2}=j \omega \mu_{0} \sigma+k^{2}\)

y señalar que los coeficientes anteriores se eligen para que no\(\ \bar{H}\) tenga divergencia.

Tenga en cuenta que si\(\ k\) es pequeño (es decir, si la longitud de onda de la excitación es grande), este coeficiente espacial\(\ \alpha\) se convierte

\(\ \alpha=\frac{1+j}{\delta}\)

donde la profundidad de la piel es:

\(\ \delta=\sqrt{\frac{2}{\omega \mu_{0} \sigma}}\)

Para obtener impedancia superficial, utilizamos la ley de Faraday:

\(\ \nabla \times \bar{E}=-\frac{\partial \bar{B}}{\partial t}\)

que da:

\(\ \underline{E}_{z}=-\mu_{0} \frac{\omega}{k} \underline{H}_{y}\)

Ahora: la “corriente superficial” es solo

\(\ \underline{K}_{s}=-\underline{H}_{x}\)

de manera que la impedancia superficial equivalente sea:

\(\ \underline{Z}=\frac{\underline{E}_{z}}{-\underline{H}_{x}}=j \mu_{0} \frac{\omega}{\alpha} \operatorname{coth} \alpha T\)

Un par de límites son interesantes aquí. Suponiendo que la longitud de onda es larga, por lo que\(\ k\) es insignificante, entonces si\(\ \alpha T\) es pequeña (es decir, material delgado),

\(\ \underline{Z} \rightarrow j \mu_{0} \frac{\omega}{\alpha^{2} T}=\frac{1}{\sigma T}\)

Por otra parte\(\ \alpha T \rightarrow \infty\), como,

\(\ \underline{Z} \rightarrow \frac{1+j}{\sigma \delta}\)

A continuación es necesario transferir esta impedancia superficial a través del entrehierro de una máquina. Entonces, con referencia a la Figura 8, supongamos un nuevo sistema de coordenadas en el que\(\ \underline{Z}_{s}\) se ubica la superficie de impedancia\(\ y=0\), y deseamos determinar la impedancia\(\ \underline{Z}=-\underline{E}_{z} / \underline{H}_{x}\) a\(\ y=g\).

En la brecha no hay corriente, por lo que el campo magnético se puede expresar como el gradiente de un potencial escalar que obedece a la ecuación de Laplace:

\(\ \bar{H}=-\nabla \psi\)

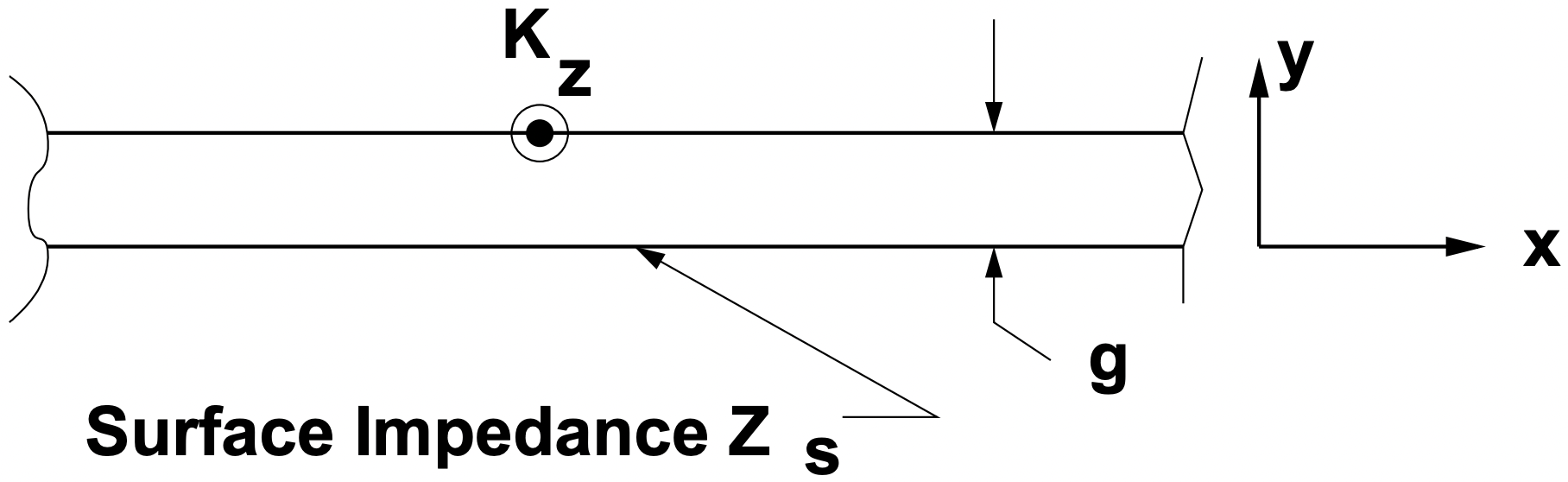Figura 8: Impedancia a través del entrehierro

y

\(\ \nabla^{2} \psi=0\)

Ignorando un factor común de\(\ e^{j(\omega t-k x)}\), podemos expresarnos\(\ \bar{H}\) en la brecha como:

\ (\\ begin {array} {l}
\ subrayado {H} _ {x} =j k\ izquierda (\ subrayado {\ psi} _ {+} e^ {k y} +\ subrayado {\ psi} _ {-} e^ {-k y}\ derecha)\
\ subrayado {H} _ {y} =-k\ izquierda (\ subrayado {\ psi} _ {+} e^ {k y} -\ subrayado {\ psi} _ {-} e^ {-k y}\ derecha)
\ end {array}\)

En la superficie del rotor,

\(\ \underline{E}_{z}=-\underline{H}_{x} \underline{Z}_{s}\)

o

\(\ -\omega \mu_{0}\left(\underline{\psi}_{+}-\underline{\psi}_{-}\right)=j k \underline{Z}_{s}\left(\underline{\psi}_{+}+\underline{\psi}_{-}\right)\)

y luego, en la superficie del estator,

\(\ \underline{Z}=-\frac{\underline{E}_{z}}{\underline{H}_{x}}=j \mu_{0} \frac{\omega}{k} \frac{\underline{\psi}_{+} e^{k g}-\underline{\psi}_{-} e^{-k g}}{\underline{\psi}_{+} e^{k g}+\underline{\psi}_{-} e^{-k g}}\)

Se requiere un poco de manipulación para obtener:

\(\ \underline{Z}=j \mu_{0} \frac{\omega}{k}\left\{\frac{e^{k g}\left(\omega \mu_{0}-j k \underline{Z}_{s}\right)-e^{-k g}\left(\omega \mu_{0}+j k \underline{Z}_{s}\right)}{e^{k g}\left(\omega \mu_{0}-j k \underline{Z}_{s}\right)+e^{-k g}\left(\omega \mu_{0}+j k \underline{Z}_{s}\right)}\right\}\)

Es útil señalar que, en el límite de\(\ \underline{Z}_{s} \rightarrow \infty\), esta expresión se acerca a la impedancia de gap

\(\ \underline{Z}_{g}=j \frac{\omega \mu_{0}}{k^{2} g}\)

y, si la brecha es lo suficientemente pequeña que\(\ k g \rightarrow 0\),

\(\ \underline{Z} \rightarrow \underline{Z}_{g} \| \underline{Z}_{s}\)