8.5: Hierro

Las máquinas eléctricas emplean materiales ferromagnéticos para transportar flujo magnético desde y hacia lugares apropiados dentro de la máquina. Dichos materiales tienen propiedades interesantes, útiles y problemáticas, y los diseñadores de máquinas eléctricas deben ocuparse de estas cosas. El propósito de esta nota es introducir las propiedades más sobresalientes de los tipos de materiales magnéticos utilizados en las máquinas eléctricas.

Aquí nos ocuparemos de materiales que exhiben magnetización: la densidad de flujo es otra cosa que\(\ \vec{B}=\mu_{0} \vec{H}\). Generalmente, hablaremos de materiales magnéticos duros y blandos. Los materiales duros son aquellos en los que la magnetización tiende a ser permanente, mientras que los materiales blandos se utilizan en circuitos magnéticos de máquinas y transformadores eléctricos. Ya que están relacionados nos encontraremos hablando de ellos ya sea al mismo tiempo o muy cerca, aunque sus usos son ampliamente dispares.

Magnetización:

Es posible relacionar, en todos los materiales, la densidad de flujo magnético con la intensidad del campo magnético con una relación constitutiva de la forma:

\(\ \vec{B}=\mu_{0}(\vec{H}+\vec{M})\)

donde la intensidad del campo magnético H y la magnetización M son las dos propiedades importantes. Ahora, en material magnético lineal la magnetización es una función lineal simple del campo magnético:

\(\ \vec{M}=\chi_{m} \vec{H}\)

de modo que la densidad de flujo es también una función lineal:

\(\ \vec{B}=\mu_{0}\left(1+\chi_{m}\right) \vec{H}\)

Nótese que en el caso más general la susceptibilidad magnética cm podría ser un tensor, lo que lleva a que la densidad de flujo no sea colineal con intensidad de campo magnético. Pero tal relación seguiría siendo lineal. Generalmente este tipo de complejidad no tiene un efecto importante en las máquinas eléctricas.

Saturación e Histéresis

En materiales magnéticos útiles esta relación agradable no es correcta y necesitamos tomar una visión más general. No vamos a tratar aquí el cuadro microscópico, excepto para señalar que la magnetización se debe a la alineación de grupos de dipolos magnéticos, los grupos a menudo llamados dominios. Solo hay tantos dipolos magnéticos disponibles en cualquier material dado, de manera que una vez que la densidad de flujo es lo suficientemente alta, se dice que el material se satura, y la relación entre la densidad de flujo magnético y la intensidad del campo magnético es no lineal.

En la Figura 9, por ejemplo, se muestra una “curva de saturación” para una chapa de acero magnética que a veces se utiliza en maquinaria eléctrica. Tenga en cuenta que la intensidad del campo magnético está en una escala logarítmica. Si esto se trazara en coordenadas lineales la saturación parecería ser bastante abrupta.

En este punto es apropiado señalar que las unidades utilizadas en el análisis de campo magnético no siempre son las mismas ni siquiera consistentes. En casi todos los sistemas la unidad de flujo es el weber (W), que

Cortesía de United States Steel Corporation. (Acero de los Estados Unidos). U.S. Steel no acepta ninguna responsabilidad por confiar en cualquier información contenida en los gráficos mostrados anteriormente.

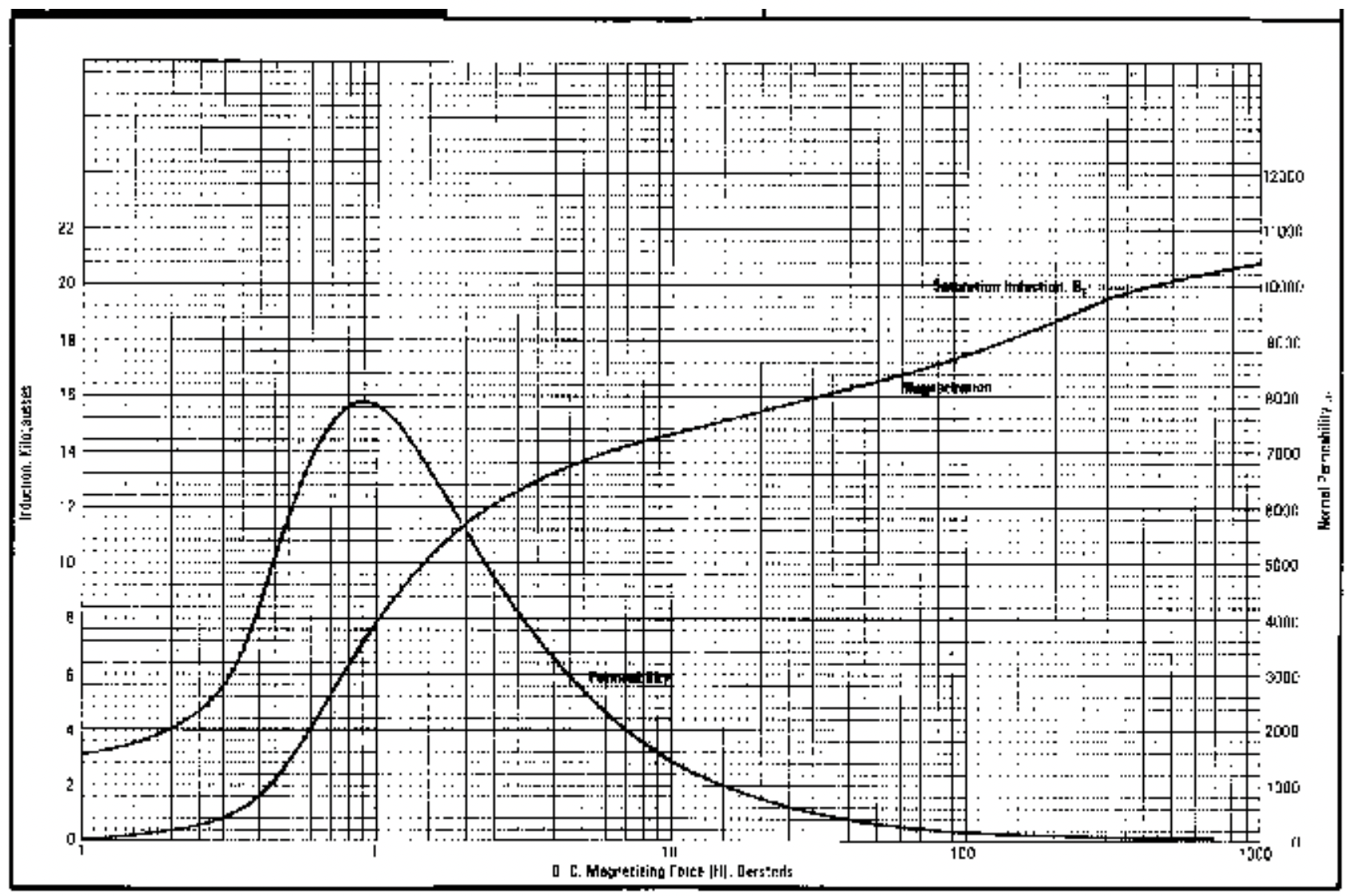
es lo mismo que un volt-segundo. En SI la unidad de densidad de flujo es la tesla (T), pero mucha gente se refiere al gauss (G), que tiene su origen en CGS. 10,000 G = 1 T. Ahora empeora, porque hay una medida del sistema inglés de densidad de flujo generalmente llamada kilo-líneas por pulgada cuadrada. Esto se debe a que en el sistema inglés la unidad de flujo es la línea. 10 ⁸ líneas es igual a un weber. Por lo tanto, un Tesla es de 64.5 kilolines por pulgada cuadrada.

Las unidades SI y CGS de densidad de flujo son fáciles de conciliar, pero las unidades de campo magnético son un poco más duras. En SI generalmente medimos H en amperios/metro (o amperios-vueltas por metro). A menudo, sin embargo, verá el campo magnético representado como Oersteds (Oe). Un Oe es lo mismo que el campo magnético requerido para producir un gauss en el espacio libre. Entonces 79.577 A/m es uno Oe.

En la mayoría de los materiales magnéticos útiles, los dominios magnéticos tienden a ser algo “pegajosos”, y se requiere un campo magnético más que incremental para que se muevan. Esto lleva a la propiedad llamada “histéresis”, tanto útil como problemática en muchos sistemas magnéticos.

Los bucles de histéresis toman muchas formas; en la Figura 10 se muestra una imagen generalizada de uno. Las características sobresalientes de la curva de histéresis son la magnetización remanente\(\ B_{r}\) y el campo coercitivo\(\ H_{c}\). Tenga en cuenta que el bucle real que se trazará es una función de la amplitud de campo y la historia. Así, hay muchos otros “bucles menores” que podrían ser trazados por la característica B-H de una pieza de material, dependiendo de lo que los campos y flujos hayan hecho y estén haciendo.

Ahora, la histéresis es importante por dos razones. Primero, representa el mecanismo para “captar” el flujo magnético en una pieza de material para formar un imán permanente. Tendremos más que decir sobre ese anon. Segundo, la histéresis es un mecanismo de pérdida. Para mostrar esto, considere algún pedazo arbitrario de

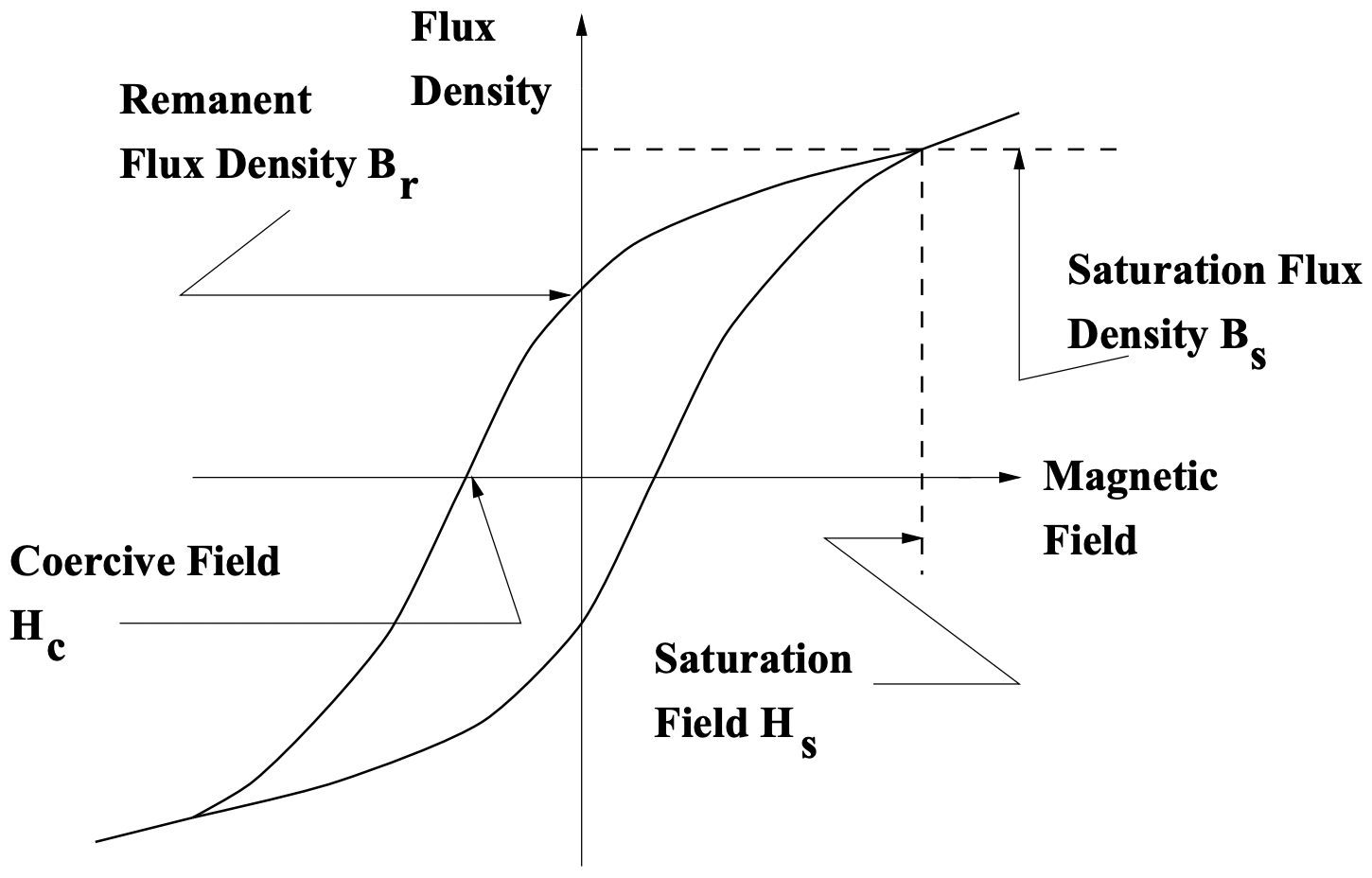Figura 10: Nomenclatura de curva de histéresis

material para el que podemos caracterizar un MMF y un flujo:

\ (\\ comenzar {alineado}
F &=N I=\ int\ vec {H}\ cdot d e\ vec {ll}\\
\ Phi &=\ int\ frac {V} {N} d t=\ iint_ {\ texto {Área}}\ vec {B}\ cdot d\ vec {A}
\ final {alineado}\)

La entrada de energía al trozo de material durante algún período de tiempo es

\(\ w=\int V I d t=\int F d \Phi=\int_{t} \int \vec{H} \cdot d \vec{\ell} \iint d \vec{B} \cdot d \vec{A} d t\)

Ahora, imagínese llevar a cabo la segunda (doble) integral sobre un conjunto continuo de superficies que son perpendiculares al campo magnético H. (¡Esto ES posible!). La energía se convierte en:

\(\ w=\int_{t} \iiint \vec{H} \cdot d \vec{B} d \mathrm{vol} d t\)

y, hecho a lo largo de un ciclo completo de alguna forma de onda de entrada, es decir:

\ (\\ comenzar {alineado}
w &=\ iiint_ {\ mathrm {vol}} W_ {m} d\ mathrm {vol}\\
W_ {m} &=\ oint_ {t}\ vec {H}\ cpunto d\ vec {B}
\ final {alineado}\)

Esa última expresión simplemente expresa el área del bucle de histéresis para el ciclo particular.

Generalmente, para la mayoría de las aplicaciones de máquinas eléctricas utilizaremos material magnético caracterizado como “blando”, teniendo un bucle de histéresis lo más estrecho posible (y por lo tanto una pérdida histéresis tan baja). En el otro extremo del espectro se encuentran materiales magnéticos “duros” que se utilizan para hacer imanes permanentes. La terminología proviene del acero, en el que el material de acero recocido blando tiende a tener bucles estrechos y el acero endurecido tiende a tener bucles más anchos. Sin embargo, la tecnología de imanes permanentes ha avanzado hasta el punto en que las fuerzas coercitivas posibles incluso en imanes cerámicos baratos superan con creces las de los aceros más duros.

Conducción, corrientes parásitas y laminaciones:

El acero, al ser un metal, es un conductor eléctrico. Así, cuando los campos magnéticos que varían en el tiempo pasan a través de él, hacen que fluyan corrientes parásitas y, por supuesto, esas producen disipación. De hecho, para casi todas las aplicaciones que involucran hierro “blando”, las corrientes parásitas son la fuente dominante de pérdida. Para reducir la pérdida de corrientes parásitas, los circuitos magnéticos de transformadores y máquinas eléctricas están casi invariablemente laminados, o compuestos por láminas de acero relativamente delgadas. Para reducir aún más las pérdidas, el acero está aleado con elementos (a menudo silicio) que envenenan la conductividad eléctrica.

Existen varios enfoques para estimar la pérdida por corrientes parásitas en chapas de acero y en la superficie de hierro sólido, y vale la pena mirar algunos de ellos. Cabe señalar que se trata de un problema “duro”, ya que el comportamiento del material en sí es difícil de caracterizar.

Estuche de Penetración Completa

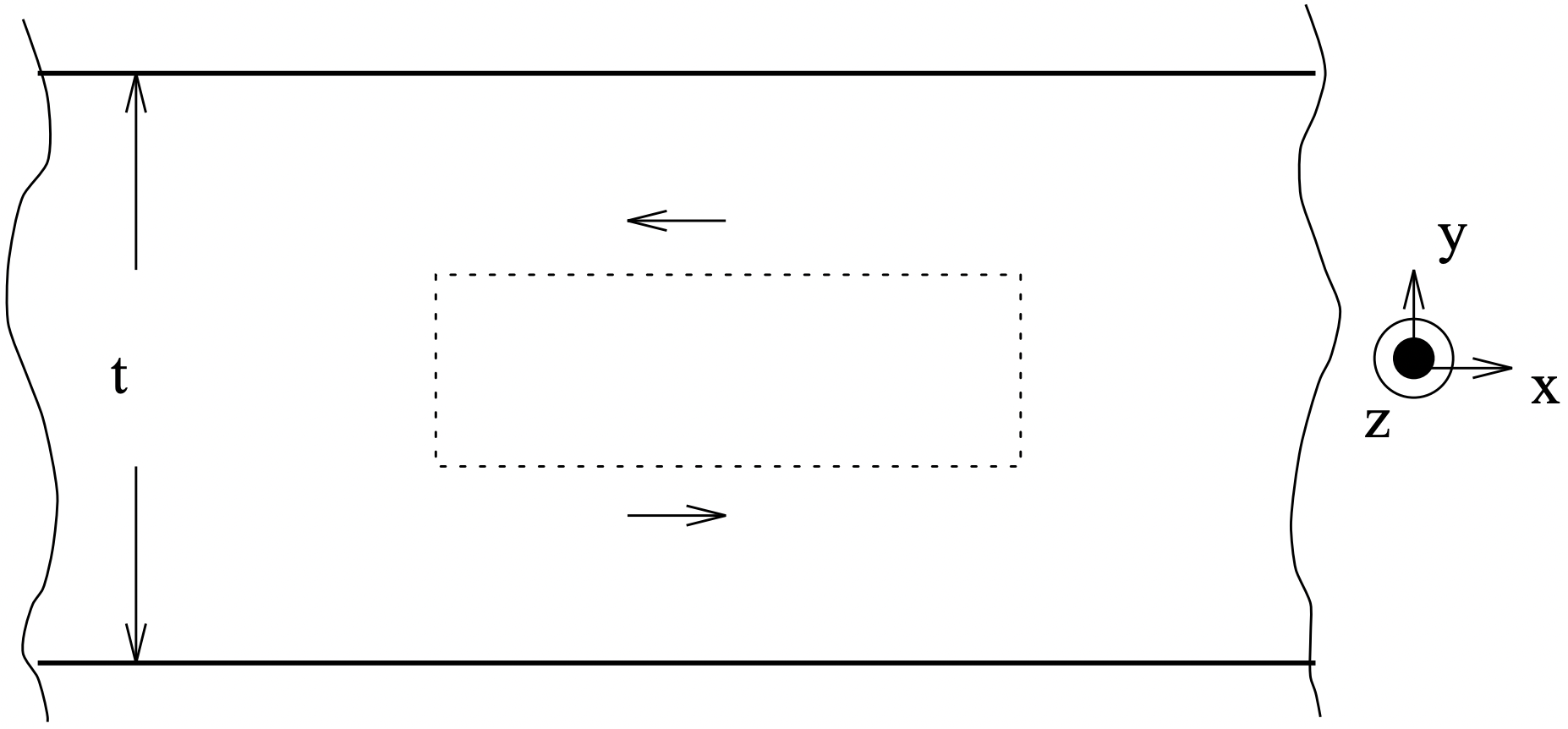Figura 11: Sección de Laminación para Cálculo de Pérdidas

Considera el problema de una pila de laminaciones. En particular, considere una hoja en la pila representada en la Figura 11. Tiene espesor\(\ t\) y conductividad\(\ \sigma\). Supongamos que la “profundidad de la piel” es mucho mayor que el grosor de la lámina para que el campo magnético penetre completamente en la lámina. Además, supongamos que la densidad de flujo magnético aplicada es paralela a la superficie de las láminas:

\(\ \vec{B}=\vec{i}_{z} \operatorname{Re}\left\{\sqrt{2} B_{0} e^{j \omega t}\right\}\)

Ahora podemos usar la ley de Faraday para determinar el campo eléctrico y por lo tanto la densidad de corriente en la lámina. Si el problema es uniforme en las direcciones x y z,

\(\ \frac{\partial \underline{E}_{x}}{\partial y}=-j \omega_{0} B_{0}\)

Tenga en cuenta también que, a menos que haya alguna corriente neta de transporte en la dirección x, E debe ser antisimétrica alrededor del centro de la lámina. Así, si tomamos el origen de y para estar en el centro, el campo eléctrico y la corriente son:

\ (\\ comenzar {alineado}
E_ {x} &=-j\ omega B_ {0} y\\
\ subrayado {J} _ {x} &=-j\ omega B_ {0}\ sigma y
\ final {alineado}\)

La energía local disipada es

\(\ P(y)=\omega^{2} B_{0}^{2} \sigma y^{2}=\frac{|J|^{2}}{\sigma}\)

Para encontrar la potencia media disipada integramos sobre el espesor de la laminación:

\(\ <P>=\frac{2}{t} \int_{0}^{\frac{t}{2}} P(y) d y=\frac{2}{t} \omega^{2} B_{0}^{2} \sigma \int_{0}^{\frac{t}{2}} y^{2} d y=\frac{1}{12} \omega^{2} B_{0}^{2} t^{2} \sigma\)

Preste atención a los órdenes de los diversos términos aquí: la potencia es proporcional al cuadrado de densidad de flujo y al cuadrado de frecuencia. También es proporcional al cuadrado del espesor de laminación (esto es la disipación de potencia volumétrica promedio).

Como un aparte, considere un circuito magnético simple hecho de este material, con cierta longitud\(\ \ell\) y área A, por lo que ese volumen de material es\(\ \ell A\). El fundente forrado por una bobina de N vueltas sería:

\(\ \Lambda=N \Phi=N A B_{0}\)

y el voltaje es, por supuesto, justo\(\ V=j w L\). La potencia total disipada en este núcleo sería:

\(\ P_{c}=A \ell \frac{1}{12} \omega^{2} B_{0}^{2} t^{2} \sigma=\frac{V^{2}}{R_{c}}\)

donde la resistencia equivalente del núcleo es ahora

\(\ R_{c}=\frac{A}{\ell} \frac{12 N^{2}}{\sigma t^{2}}\)

Corrientes Foucaicas en Hierro Saturante

La misma geometría se mantiene para este patrón, aunque consideramos solo el problema unidimensional\(\ (k \rightarrow 0)\). El problema lo trabajaron McLean y su estudiante de posgrado Ecuación Agarwal\ ref {2} Ecuación\ ref {1}. Supusieron que el campo magnético en la superficie de la losa plana de material era sinusoidal en el tiempo y de amplitud lo suficientemente alta como para saturar el material. Esto es cierto si el material tiene alta permeabilidad y el campo magnético es fuerte. Lo que sucede es que el campo magnético impresionado satura una región de material cerca de la superficie, lo que lleva a una densidad de flujo magnético paralela a la superficie. La profundidad de la región afectada cambia con el tiempo, y hay una superficie de separación (en el problema plano este es un plano) que se aleja de la superficie superior en respuesta al cambio en el campo magnético. Se desarrolla un campo eléctrico para mover la superficie, y ese campo magnético impulsa las corrientes parásitas en el material.

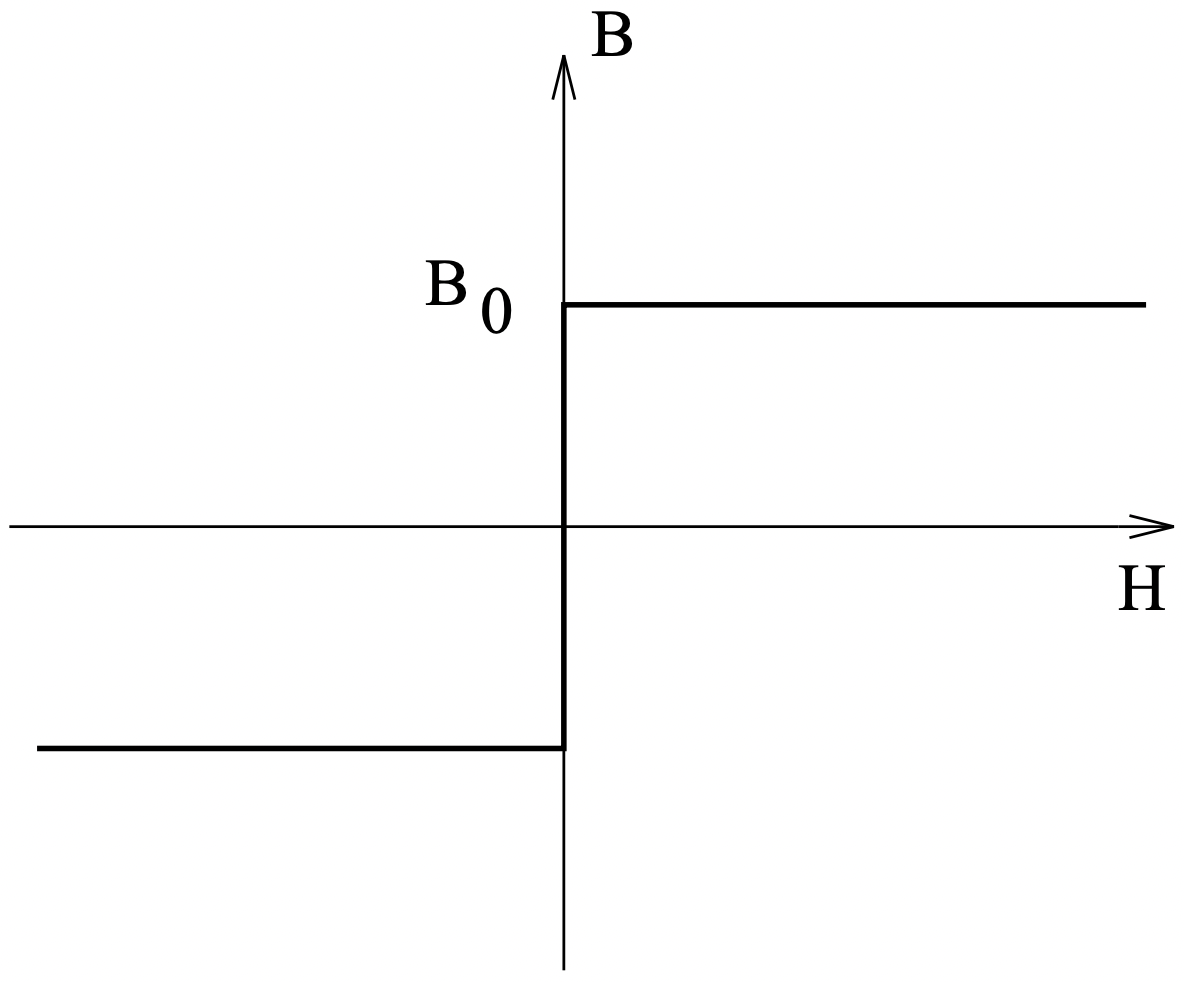Figura 12: Característica saturante idealizada

Supongamos que el material tiene una curva de magnetización perfectamente rectangular como se muestra en la Figura 12, de manera que la densidad de flujo en la dirección x es:

\(\ B_{x}=B_{0} \operatorname{sign}\left(H_{x}\right)\)

El flujo por unidad de ancho (en la dirección z) es:

\(\ \Phi=\int_{0}^{-\infty} B_{x} d y\)

y la ley de Faraday se convierte en:

\(\ E_{z}=\frac{\partial \Phi}{\partial t}\)

mientras que la ley de Ampere junto con la ley de Ohm es:

\(\ \frac{\partial H_{x}}{\partial y}=\sigma E_{z}\)

Ahora, McLean sugirió una solución a este conjunto en la que hay una “superficie de separación” a profundidad\(\ \zeta\) por debajo de la superficie, como se muestra en la Figura 13. En cualquier momento dado:

\ (\\ comenzar {alineado}
H_ {x} &=H_ {s} (t)\ izquierda (1+\ frac {y} {\ zeta}\ derecha)\\
J_ {z} &=\ sigma E_ {z} =\ frac {H_ {s}} {\ zeta}
\ final {alineado}\)

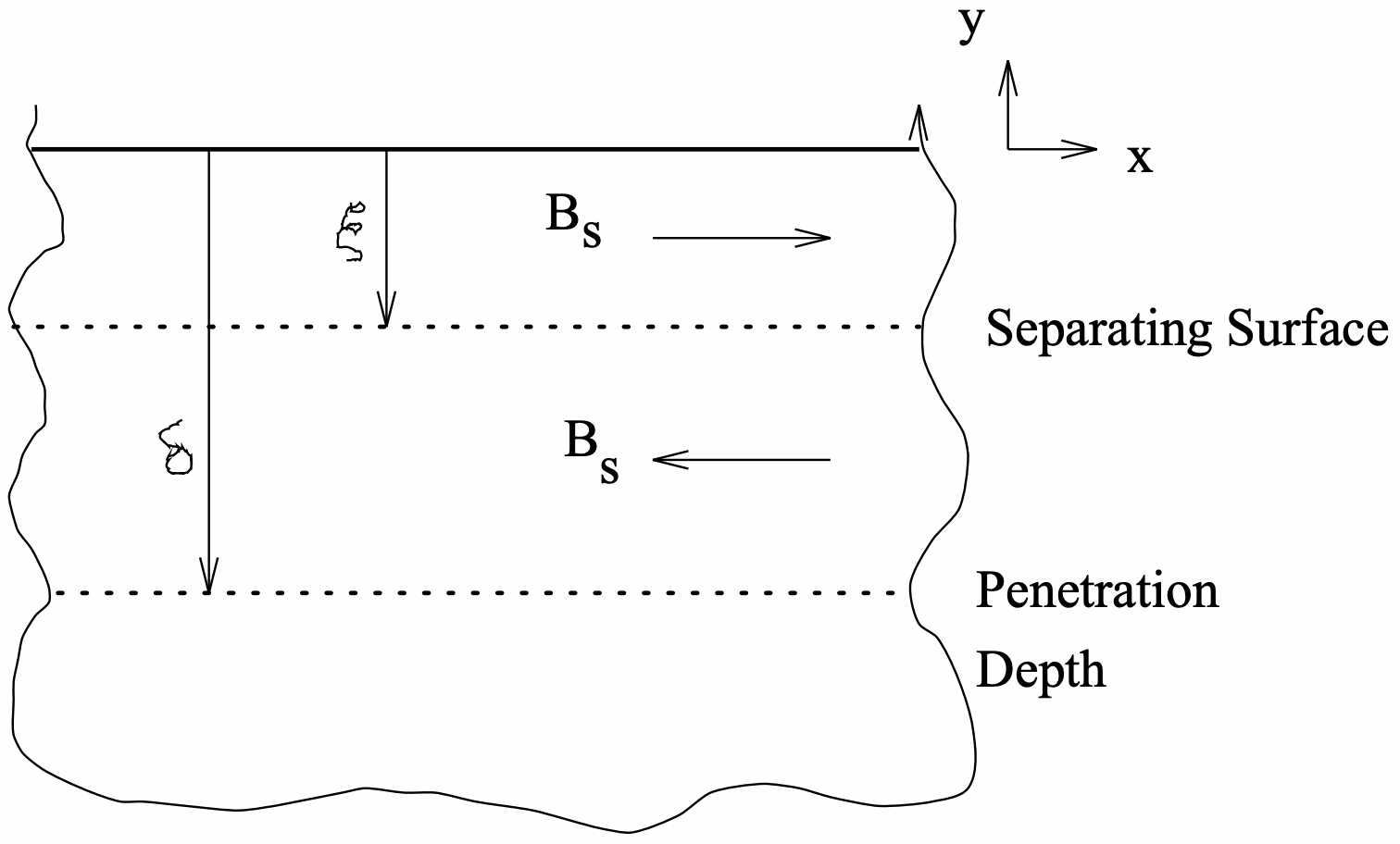Figura 13: Separación de superficie y profundidad de penetración

Es decir, en la región entre la superficie de separación y la parte superior del material, el campo eléctrico\(\ E_{z}\) es uniforme y el campo magnético\(\ H_{x}\) es una función lineal de la profundidad, cayendo de su valor de impresión en la superficie a cero en la superficie de separación. Ahora: el campo eléctrico es producido por la tasa de cambio de flujo que es:

\(\ E_{z}=\frac{\partial \Phi}{\partial t}=2 B_{x} \frac{\partial \zeta}{\partial t}\)

Eliminando E, tenemos:

\(\ 2 \zeta \frac{\partial \zeta}{\partial t}=\frac{H_{s}}{\sigma B_{x}}\)

y luego, si el campo magnético impresionado es sinusoidal, esto se convierte en:

\(\ \frac{d \zeta^{2}}{d t}=\frac{H_{0}}{\sigma B_{0}}|\sin \omega t|\)

Esto es fácil de resolver, suponiendo que\(\ \zeta=0\) en\(\ t=0\),

\(\ \zeta=\sqrt{\frac{2 H_{0}}{\omega \sigma B_{0}}} \sin \frac{\omega t}{2}\)

Ahora: la superficie siempre se mueve en dirección descendente (tal como la hemos dibujado), así que en cada medio ciclo se crea una nueva superficie: la antigua simplemente deja de moverse en una posición máxima, o profundidad de penetración:

\(\ \delta=\sqrt{\frac{2 H_{0}}{\omega \sigma B_{0}}}\)

Esta profundidad de penetración es análoga a la “profundidad de la piel” de la teoría lineal. Sin embargo, es una profundidad de penetración absoluta.

El campo eléctrico resultante es:

\(\ E_{z}=\frac{2 H_{0}}{\sigma \delta} \cos \frac{\omega t}{2} \quad 0<\omega t<\pi\)

Esto puede ser analizado por Fourier: señalando que si el campo magnético impresionado es sinusoidal, solo es importante el componente fundamental de tiempo del campo eléctrico, lo que lleva a:

\(\ E_{z}=\frac{8}{3 \pi} \frac{H_{0}}{\sigma \delta}(\cos \omega t+2 \sin \omega t+\ldots)\)

La impedancia superficial compleja es la relación entre la amplitud compleja del campo eléctrico y magnético, que se convierte en:

\(\ \underline{Z}_{s}=\frac{\underline{\underline{E}_{z}}}{\underline{H}_{x}}=\frac{8}{3 \pi} \frac{1}{\sigma \delta}(2+j)\)

Así, en aplicaciones prácticas, podemos manejar esta superficie tanto como manejamos superficies conductoras lineales, estableciendo una profundidad de piel y asumiendo que la corriente fluye dentro de esa profundidad de piel de la superficie. La resistencia se modifica por el factor de\(\ \frac{16}{3 \pi}\) y el “factor de potencia” de esta superficie es de aproximadamente 89% (a diferencia de una superficie lineal donde el “factor de potencia” es de aproximadamente 71%.

Agarwal sugiere usar un valor\(\ B_{0}\) de aproximadamente el 75% de la densidad de flujo de saturación del acero.