8.6: Método Semiempírico de Manejo de la Pérdida de Hierro
- Page ID
- 85342
Ninguno de los modelos descritos hasta ahora es totalmente satisfactorio para describir el comportamiento del hierro laminado, ya que las pérdidas son una combinación de pérdidas por corrientes de Foucay por histéresis. El modelo bastante simple empleado para las corrientes de Foucault es preciso debido a su suposición de saturación abrupta. El modelo de histéresis, aunque preciso, requeriría una determinación empírica del tamaño de los bucles de histéresis de todos modos. Por lo que a menudo debemos recurrir a datos empíricos de pérdida. Los fabricantes de láminas de acero laminadas publicarán datos, generalmente en forma de curvas, para muchos de sus productos. Aquí hay algunas formas de ver los datos.
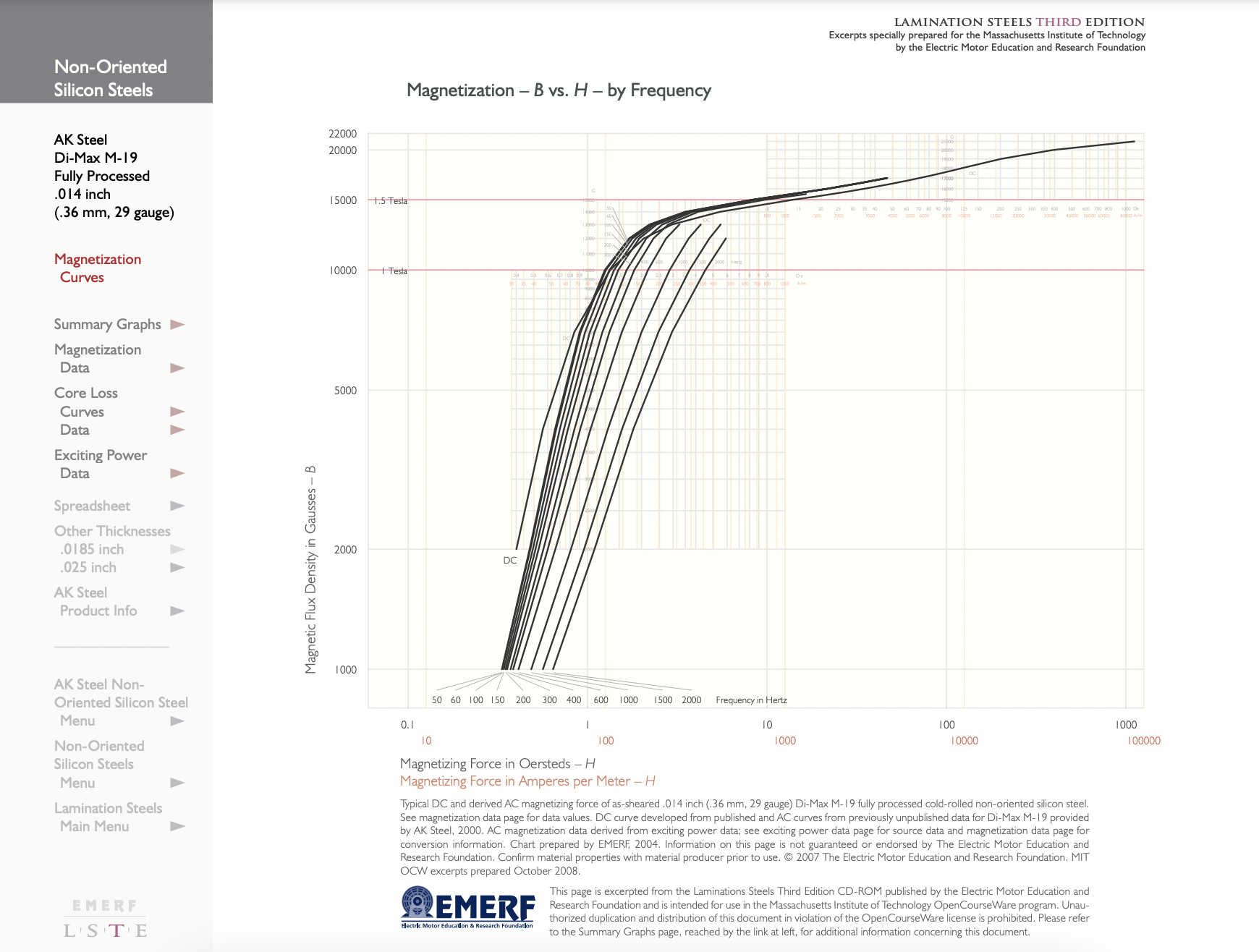
En la Figura 9 se muestra una curva de densidad de flujo de baja frecuencia vs. campo magnético (“saturación”). Con eso se incluyó una medida de la permeabilidad incremental
\(\ \mu^{\prime}=\frac{d B}{d H}\)
En algunas aplicaciones de máquinas se requiere la inductancia “total” (relación de flujo a MMF) o inductancia “incremental” (pendiente del flujo a la curva MMF). En el límite de baja frecuencia estos números pueden ser útiles.
Para diseñar máquinas eléctricas, sin embargo, una segunda forma de ver el acero puede ser más útil. Esto es para medir la potencia real y reactiva en función de la densidad del flujo magnético y (a veces) la frecuencia. En principio, estos datos son inmediatamente útiles. En cualquier máquina eléctrica bien diseñada, la densidad de flujo en el núcleo se distribuye de manera bastante uniforme y no se ve fuertemente afectada por las corrientes parásitas, etc. en el núcleo. Bajo tales circunstancias se puede determinar la densidad de flujo en cada parte del núcleo. Con esa información se puede ir a los datos empíricos publicados para la potencia real y reactiva y determinar la pérdida del núcleo y los requisitos de potencia reactiva.
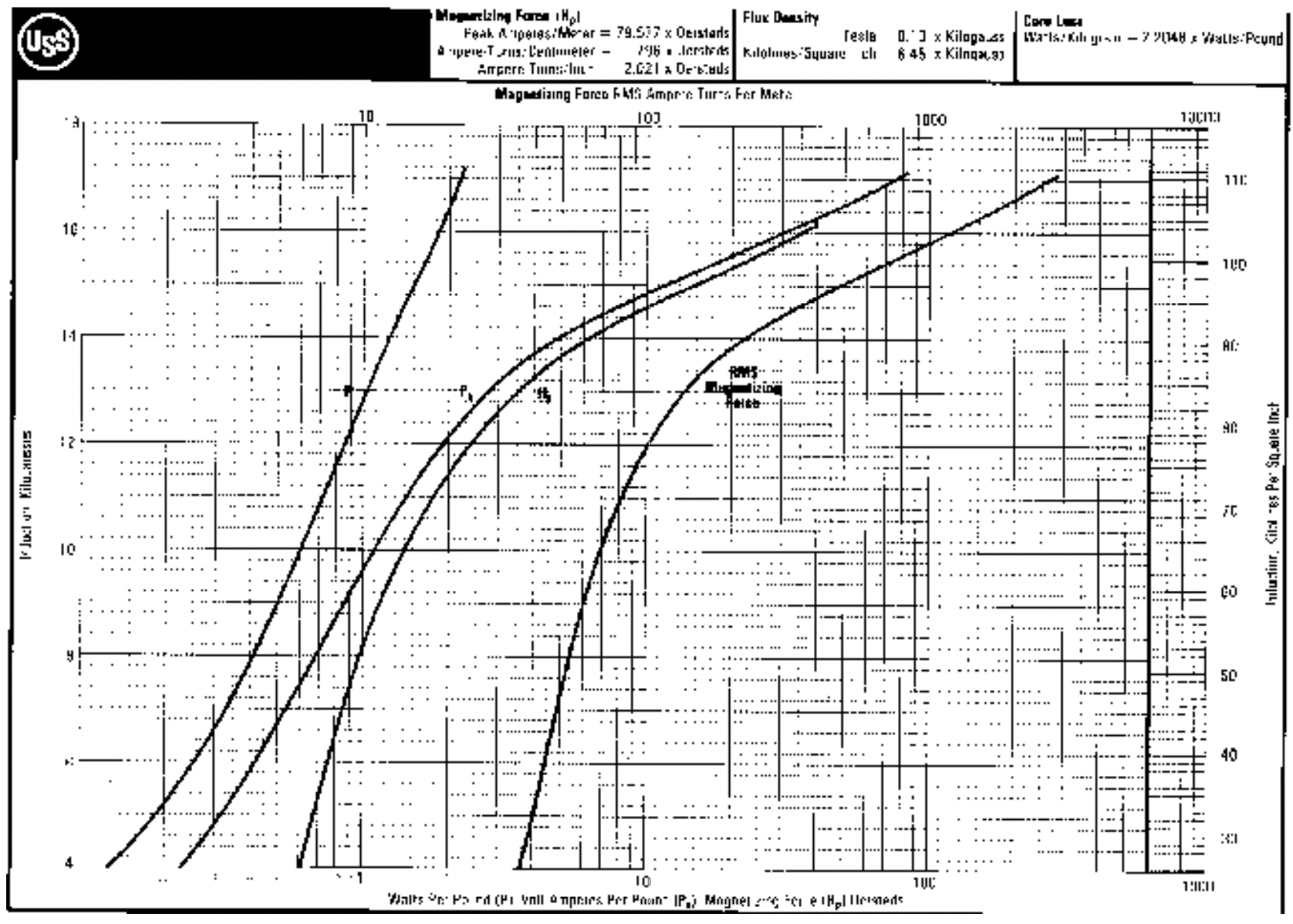
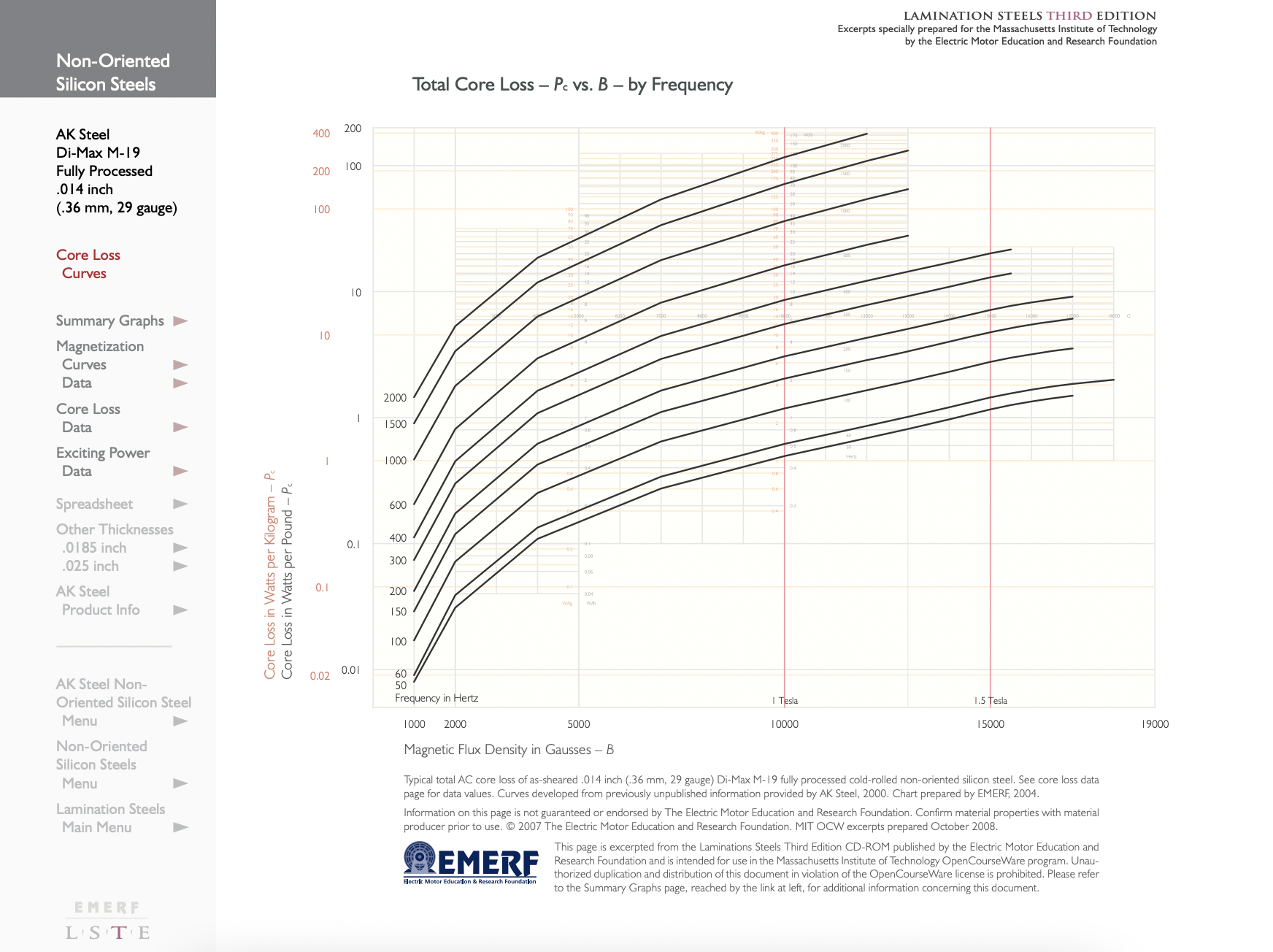
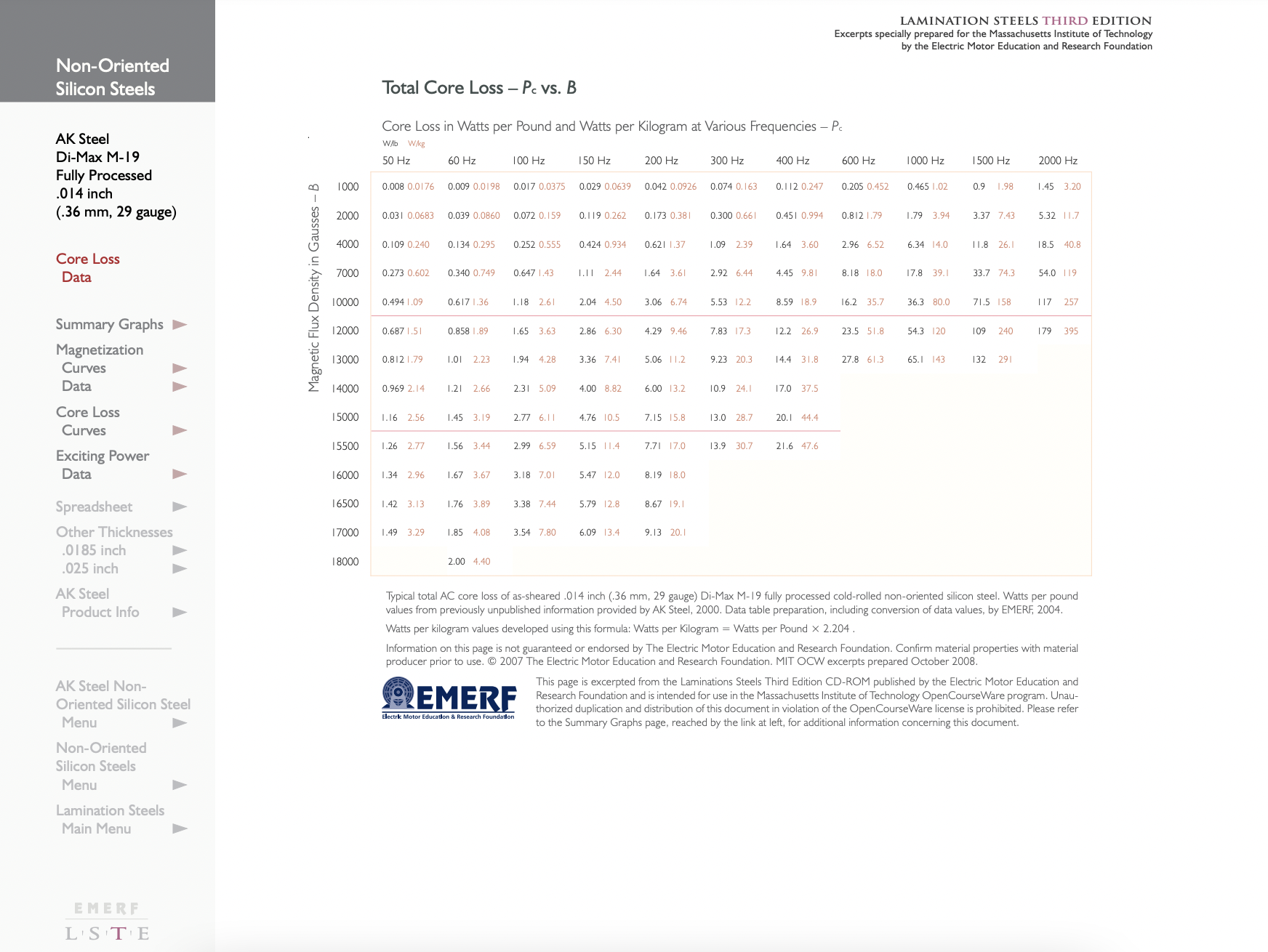
La Figura 14 muestra la pérdida de núcleo y la potencia “aparente” por unidad de masa en función de la inducción (RMS) para acero M-19 completamente procesado de calibre 29. Las dos curvas de la izquierda son las que más nos resultarán útiles. “\(\ P\)" denota poder real mientras "\(\ P_{a}\)" denota “poder aparente”. El uso de estos datos es bastante sencillo. Si se estima la densidad de flujo en una máquina para cada parte de la máquina y se calcula la masa de acero, entonces con la ayuda de este gráfico una pérdida total del núcleo y la potencia aparente pueden
| M-19 | M-36 | ||
| Densidad de flujo base | \(\ B_{0}\) | 1 T | 1 T |
| Frecuencia Base | \(\ f_{0}\) | 60 Hz | 60 Hz |
| Potencia Base (w/lb) | \(\ P_{0}\) | 0.59 | 0.67 |
| Exponente de flujo | \(\ \epsilon_{B}\) | 1.88 | 1.86 |
| Exponente de frecuencia | \(\ \epsilon_{F}\) | 1.53 | 1.48 |
| Base de potencia aparente 1 | \(\ V A_{0}\) | 1.08 | 1.33 |
| Base de potencia aparente 2 | \(\ V A_{1}\) | .0144 | .0119 |
| Exponente de flujo | \(\ \epsilon_{0}\) | 1.70 | 2.01 |
| Exponente de flujo | \(\ \epsilon_{1}\) | 16.1 | 17.2 |
ser estimado. Entonces el efecto del núcleo puede aproximarse con un par de elementos en paralelo con los terminales, con:
\ (\\ comenzar {alineado}
R_ {c} &=\ frac {Q|v|^ {2}} {P}\\
X_ {c} &=\ frac {Q|v|^ {2}} {Q}\\
Q &=\ sqrt {P_ {a} ^ {2} -P^ {2}}
\ end {alineado}\)
Dónde\(\ q\) está el número de fases de la máquina y\(\ V\) es el voltaje de fase. Tenga en cuenta que esta imagen es, estrictamente hablando, solo válida para la tensión y frecuencia para la que se calculó la densidad de flujo. Pero será aproximadamente cierto para pequeñas excursiones ya sea en voltaje o frecuencia y por lo tanto útil para estimar la caída de voltaje debido a la corriente excitante y tales asuntos. En aplicaciones de programas de diseño, estos parámetros se pueden volver a calcular repetidamente si es necesario.
“Buscar” estos datos es incómodo para los estudios de diseño, por lo que a menudo es conveniente hacer un “ajuste de curva” a los datos publicados. Hay una gran cantidad de formas posibles de hacer esto. Un método que se ha encontrado que funciona razonablemente bien para el hierro de silicio es un “ajuste exponencial”:
\(\ P \approx P_{0}\left(\frac{B}{B_{0}}\right)^{\epsilon_{B}}\left(\frac{f}{f_{0}}\right)^{\epsilon_{F}}\)
Este ajuste es apropiado si los datos aparecen en una gráfica logarítmica y logarítmica se encuentran aproximadamente en líneas rectas. La figura 15 muestra tal ajuste para la misma chapa de acero que las otras figuras.
Para el “poder aparente” se puede utilizar el mismo tipo de método. Parece, sin embargo, que el ajuste exponencial simple que funciona bien para la potencia real es inadecuado, al menos si se van a utilizar inducciones relativamente altas. Esto se debe a que, a medida que el acero se satura, el componente reactivo de la corriente excitante se eleva rápidamente. He tenido cierto éxito con un ajuste “doble exponencial”:
\(\ V A \approx V A_{0}\left(\frac{B}{B_{0}}\right)^{\epsilon_{0}}+V A_{1}\left(\frac{B}{B_{0}}\right)^{\epsilon_{1}}\)
A primer orden, el componente reactivo de la corriente excitante será lineal en frecuencia.
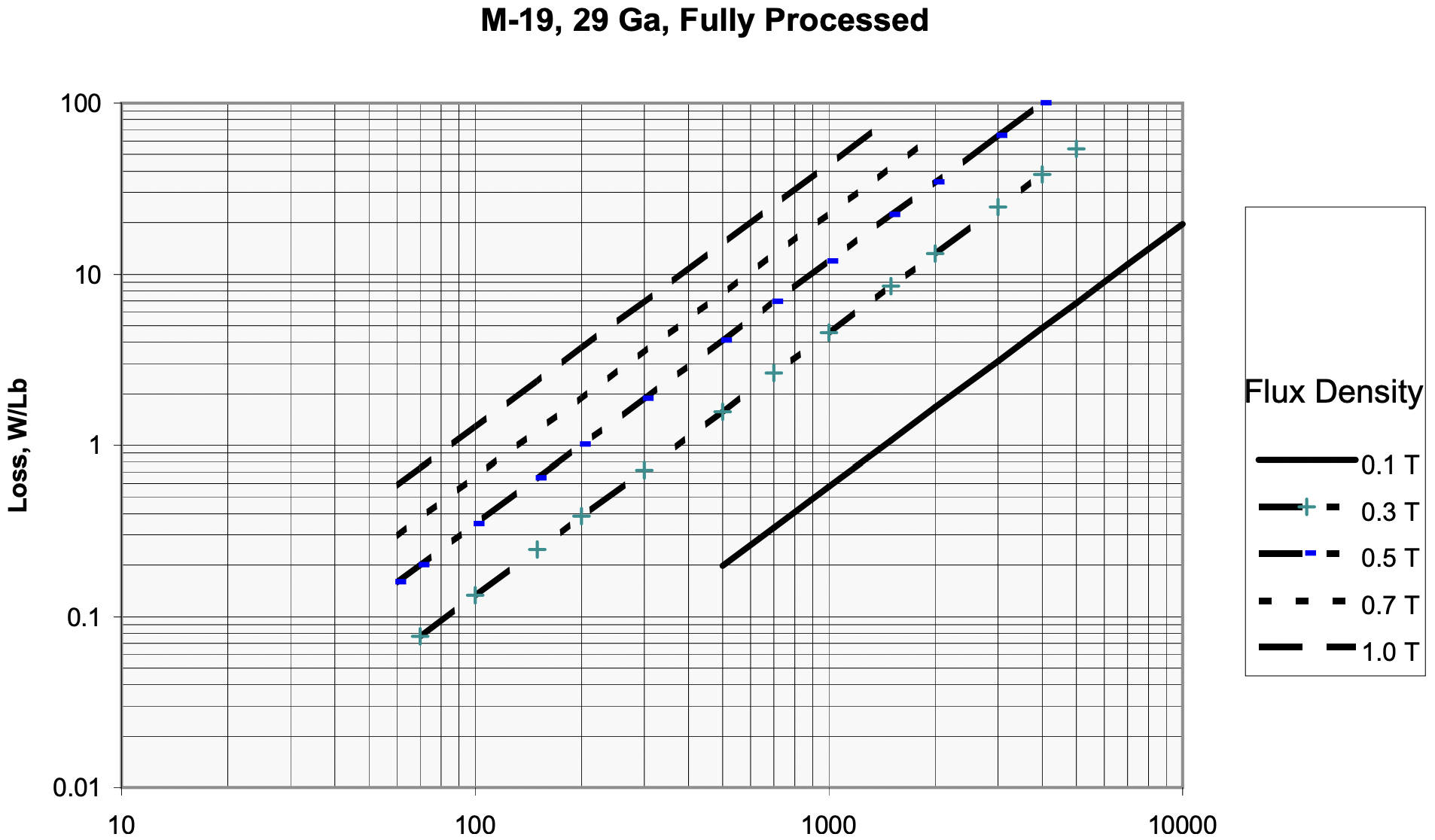Figura 15: Ajuste de pérdida de núcleo de chapa de acero frente a densidad de flujo y frecuenciaEn el disco que se va a distribuir con estas notas hay una serie de archivos de datos que representan propiedades de diferentes tipos de chapa de acero no orientado. El formato de cada uno de los archivos es el mismo: dos columnas de números, la primera es la densidad de flujo en Tesla, RMS, 60 Hz. La segunda columna es de vatios por libra o vo). Proc es “f” para procesado completo y “s” para semiprocesado. Los datos son “p” para el poder, “pa” para el poder aparente. El calibre es de 29 (.014” de grosor), 26 (.0185” de grosor) o 24 (.025” de grosor). Ejemplo: m19fp29.prn designa pérdida en material M-19, completamente procesado, calibre 29.
También en el disco hay tres rutinas de ajuste de curvas que parecen funcionar con estos datos. (¡No todas las rutinas funcionan con todos los datos!). Ellos son:
efit<return>.encajar lo que (nombre.prn) ==>Ingrese el nombre de archivo para el designador de material sin la extensión
.prn. El programa pensará en el problema durante unos segundos y pondrá una gráfica de su ajuste con puntos anotando los datos reales. Ingrese a<return>y un resumen de las vueltas de ajuste, incluidos los parámetros de ajuste y una indicación de error. Estos programas utilizan la rutina fmins de MATLAB para minimizar un error cuadrático medio calculado por la función auxiliarfiterr.m.e2fit.mimplementa el ajuste exponencial doble de la potencia aparente contra la densidad de flujo. El uso es igual que efit. Utiliza la función auxiliarfit2err.m.pfit.mutiliza la función de MATLAB polyfit para ajustar un polinomio (en B) a los datos.
La mayoría de los guiones de diseño de máquinas incluidos con el material para este tema especial de verano emplean los ajustes exponenciales para el hierro central desarrollados aquí.
Referencias
Ecuación\ ref {1} W. MacLean, “Teoría de las Ondas Electromagnéticas Fuertes en Hierro Masivo”, Revista de Física Aplicada, V.25, No 10, Octubre, 1954
Ecuación\ ref {2} P.D. Agarwal, “Pérdidas por corrientes parásitas en hierro sólido y laminado”, Trans. AIEE, V. 78, pp 169-171, 1959
