9.6: Operación balanceada

Ahora, supongamos que la máquina funciona de esta manera: el rotor gira a una velocidad constante, la corriente de campo se mantiene constante, y las tres corrientes del estator son sinusoides en el tiempo, con la misma amplitud y con fases que difieren en 120 grados.

\ (\\ comenzar {alineado}
p\ phi &=\ omega t+\ delta_ {i}\\
i_ {f} &=I_ {f}\\
i_ {a} &=I\ cos (\ omega t)\\
i_ {b} &=I\ cos\ izquierda (\ omega t-\ frac {2\ pi} {3}\ derecha)\
i_ {c} &=I\ cos\ izquierda (\ omega t+\ frac {2\ pi} {3}\ derecha)
\ end {alineado}\)

La manipulación sencilla (pero tediosa) produce una expresión para el par:

\(\ T=-\frac{3}{2} p M I I_{f} \sin \delta_{i}\)

Operada de esta manera, con corrientes equilibradas y con la velocidad mecánica consistente con la frecuencia eléctrica\(\ (p \Omega=\omega)\), la máquina exhibe un par constante. El ángulo de fase\(\ \delta_{i}\) se llama ángulo de torsión, pero es importante tener cierta precaución, ya que hay más de un ángulo de torsión.

Ahora, mira la máquina desde los terminales eléctricos. El flujo unido por la Fase A será:

\(\ \lambda_{a}=L_{a} i_{a}+L_{a b} i_{b}+L_{a c} i_{c}+M I_{f} \cos p \phi\)

Al señalar que la suma de las corrientes de fase es, en condiciones equilibradas, cero y que las inductancias mutuas de fase fase son iguales, esto simplifica a:

\(\ \lambda_{a}=\left(L_{a}-L_{a b}\right) i_{a}+M I_{f} \cos p \phi=L_{d} i_{a}+M I_{f} \cos p \phi\)

donde usamos la notación\(\ L_{d}\) para denotar inductancia síncrona.

Ahora bien, si la máquina está girando a una velocidad consistente con la frecuencia eléctrica decimos que está operando sincrónicamente, y es posible emplear notación compleja en el estado estacionario sinusoidal. Entonces, tenga en cuenta:

\(\ i_{a}=I \cos \left(\omega t+\theta_{i}\right)=\operatorname{Re}\left\{I e^{j \omega t+\theta_{i}}\right\}\)

Si, podemos escribir una expresión para la compleja amplitud del flujo como:

\(\ \lambda_{a}=\operatorname{Re}\left\{\underline{\Lambda}_{a} e^{j \omega t}\right\}\)

donde hemos utilizado esta notación compleja:

\ (\\ comenzar {alineado}
\ subrayado {I} &=I e^ {j\ theta_ {i}}\
\ subrayado {I} _ _ {f} &=I_ {f} e^ {j\ theta_ {m}}
\ end {alineado}\)

Ahora bien, si buscamos voltaje terminal de este sistema, es:

\(\ v_{a}=\frac{d \lambda_{a}}{d t}=\operatorname{Re}\left\{j \omega \underline{\Lambda}_{a} e^{j \omega t}\right\}\)

Este sistema es descrito por el circuito equivalente que se muestra en la Figura 2.

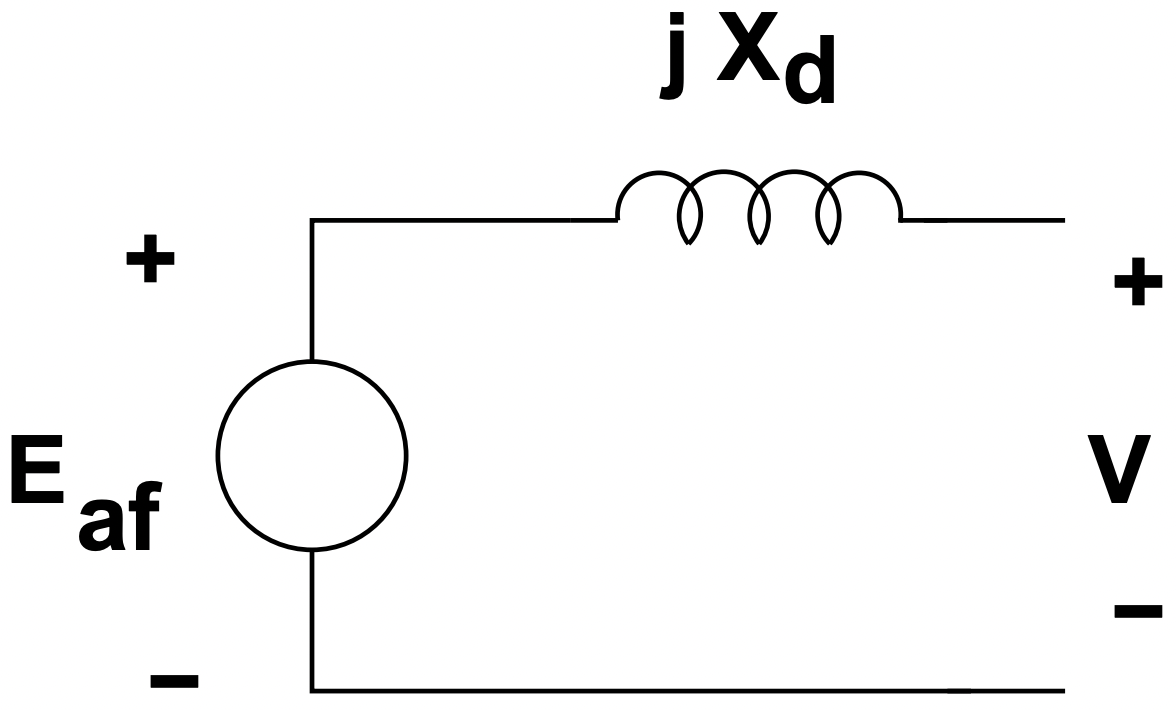Figura 2: Circuito equivalente a máquina sincrónica de rotor redondo

donde la tensión interna es:

\(\ \underline{E}_{a f}=j \omega M I_{f} e^{j \theta_{m}}\)

Ahora, si eso está conectado a una fuente de voltaje (es decir, si es fija), la corriente del terminal es:

\(\ \underline{I}=\frac{\underline{V}-E_{a f} e^{j \delta}}{j X_{d}}\)

donde\(\ X_{d}=\omega L_{d}\) está la reactancia síncrona.

Entonces la potencia real y reactiva (en la fase A) son:

\ (\\ comenzar {alineado}
P+j Q &=\ frac {1} {2}\ subrayado {V I^ {*}}\\
&=\ frac {1} {2}\ subrayado {V}\ izquierda (\ frac {\ subrayado {V} -E_ {a f} e^ {j\ delta}} {j X_ {d}\ derecha) ^ {*}\\
&=\ frac {1} {2}\ frac {|\ subrayado {V} |^ {2}} {-j X_ {d}} -\ frac {1} {2}\ frac {V E_ {a f} e^ {j\ delta}} {-j X_ {d}}
\ final {alineado}\)

Esto hace que el poder real y reactivo:

\ (\\ begin {alineado}
P_ {a} &=-\ frac {1} {2}\ frac {V E_ {a f}} {X_ {d}}\ sin\ delta\
Q_ {a} &=\ frac {1} {2}\ frac {V^ {2}} {X_ {d}} -\ frac {1} {2} frac {V E_ {a f} X_ {d}} {\ cos}\ delta
\ end {alineado}\)

Si consideramos las tres fases, el poder real es

\(\ P=-\frac{3}{2} \frac{V E_{a f}}{X_{d}} \sin \delta\)

Ahora, por fin tenemos que mirar el funcionamiento real de estas máquinas, que pueden servir ya sea como motores o como generadores.

Los diagramas vectoriales que describen el funcionamiento como motor y como generador se muestran en las Figuras 3 y 4, respectivamente.

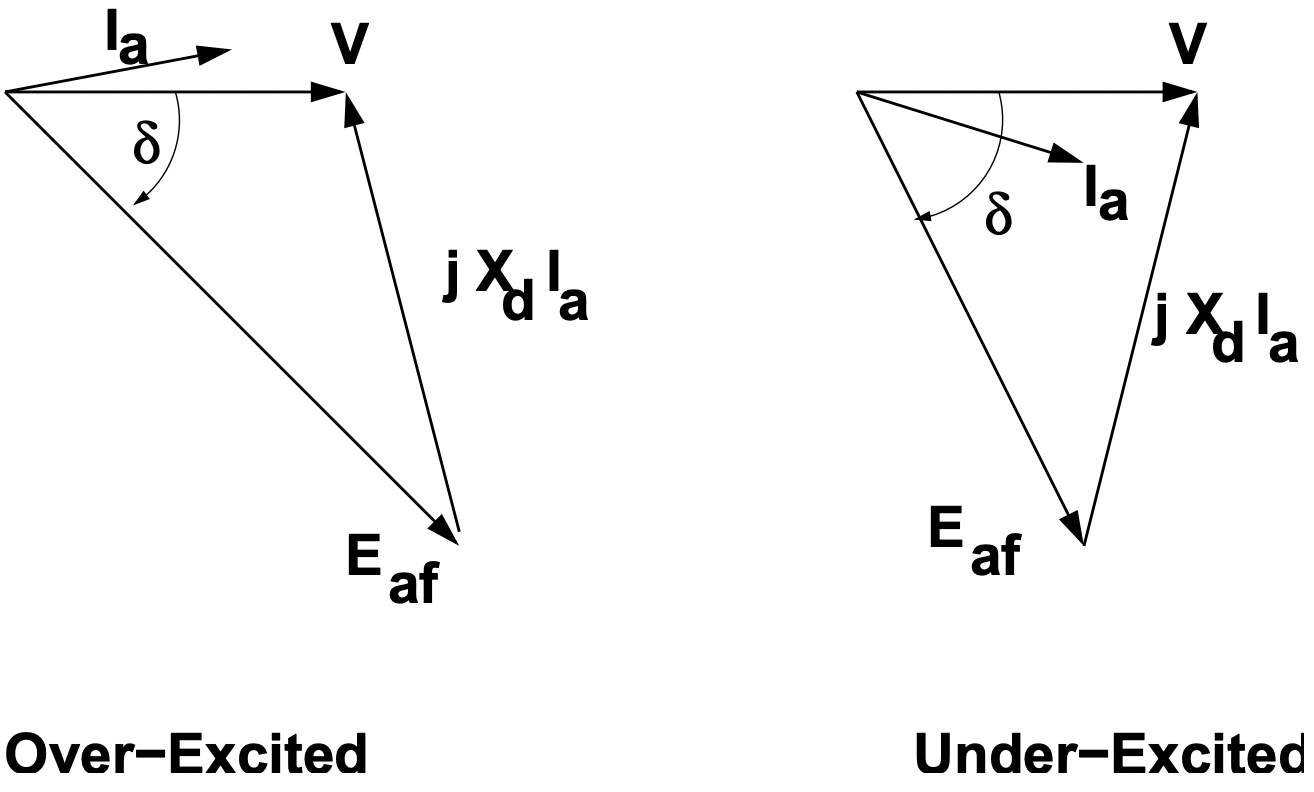Figura 3: Funcionamiento del motor, bajo y sobreexcitado

La operación como generador no es muy diferente de la operación como motor, pero es común hacer anotaciones con la corriente terminal dada el signo opuesto (“generador”).

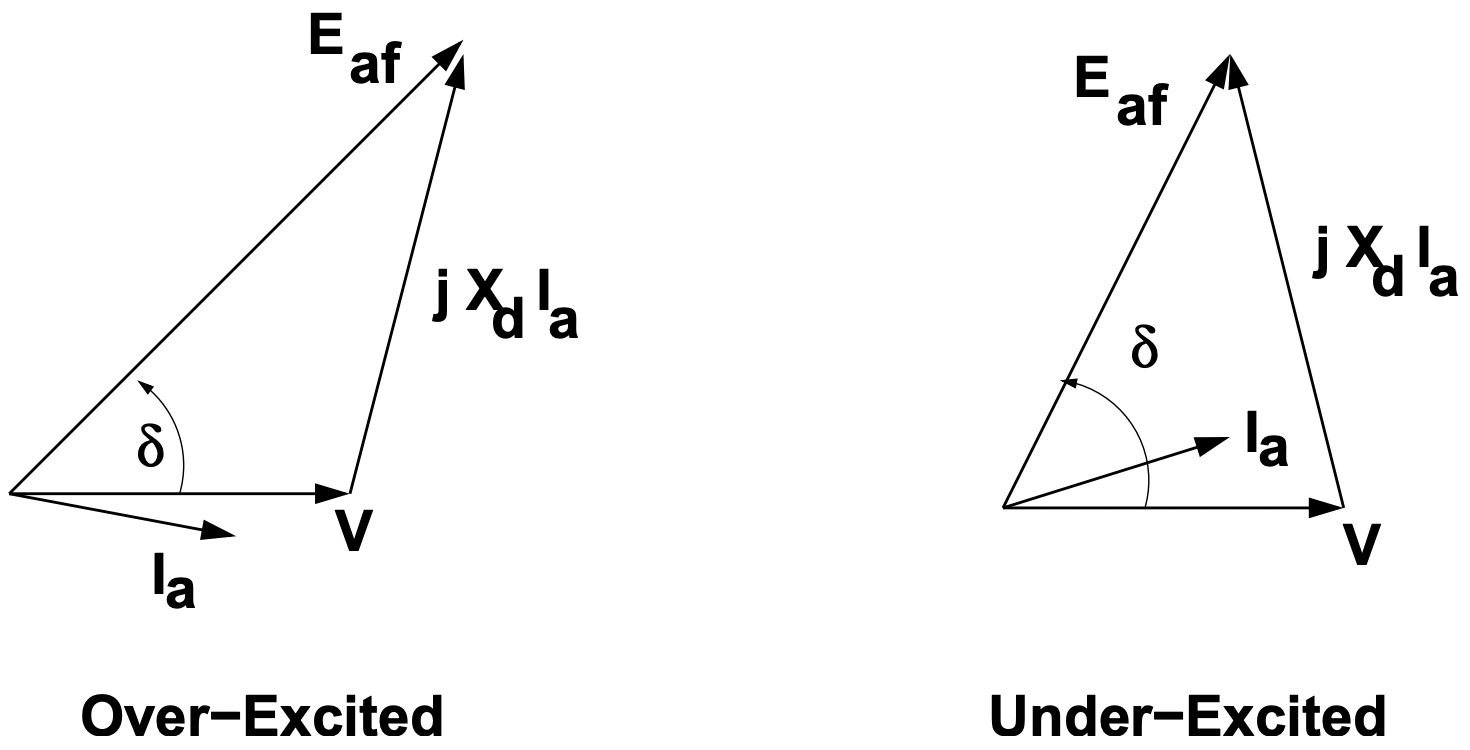Figura 4: Funcionamiento del generador, bajo y sobreexcitado