Saltar al contenido principal
LibreTexts Español

10: Evaluación analítica del diseño de máquinas de inducción

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    85482

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Introducción

    Las máquinas de inducción son quizás las más utilizadas de todos los motores eléctricos. Generalmente son simples de construir y robustos, ofrecen un rendimiento asíncrono razonable: una curva manejable de par-velocidad, operación estable bajo carga y eficiencia generalmente satisfactoria. Debido a que son tan ampliamente utilizados, vale la pena entenderlos.

    Además de su importancia económica actual, los motores de inducción y generadores pueden encontrar aplicación en algunas aplicaciones nuevas con diseños que no son similares a los motores actualmente en el comercio. Un ejemplo son los motores de muy alta velocidad para compresores de gas, quizás con rotores de jaula de ardilla, quizás con hierro sólido (o quizás con ambos).

    Debido a que es posible que en el futuro, se requiera que las máquinas de inducción de alto rendimiento tengan características diferentes a las de las máquinas existentes, es necesario entenderlas desde los primeros principios, y ese es el objetivo de este documento. Se inicia con una vista teórica de circuito de la máquina de inducción. Este análisis es estrictamente apropiado solo para máquinas de rotor de heridas, pero conduce a una comprensión de máquinas más complejas. Este modelo se utilizará para explicar el funcionamiento básico de las máquinas de inducción. Entonces derivaremos un modelo para máquinas de jaula de ardilla. Finalmente, mostraremos cómo se pueden construir modelos para máquinas de rotor sólido y rotor/jaula de ardilla sólidas mixtas.

    La visión que vamos a tomar en este documento es implacablemente clásica. Todos los elementos que usaremos se calculan a partir de los primeros principios, y no recurrimos al análisis numérico ni a métodos empíricos a menos que no tengamos otra opción. Si bien esto puede parecer seriamente limitante, sirve a nuestro objetivo básico aquí, que es lograr una comprensión de cómo funcionan estas máquinas. Tenemos la sensación de que una vez que exista esa comprensión, será posible emplear métodos de análisis más sofisticados para obtener resultados más precisos para aquellos elementos de las máquinas que no se prestan a un análisis simple.

    En la Figura 1 se muestra una imagen elemental de la máquina de inducción. El rotor y el estator son coaxiales. El estator tiene un devanado polifásico en ranuras. El rotor tiene un devanado o una jaula, también en ranuras. Esta imagen se modificará ligeramente cuando lleguemos a hablar de máquinas de “rotor sólido”, anon. Generalmente, este análisis se realiza asumiendo tres fases. Como ocurre con muchos sistemas, esto generaliza a diferentes números de fases con poca dificultad.

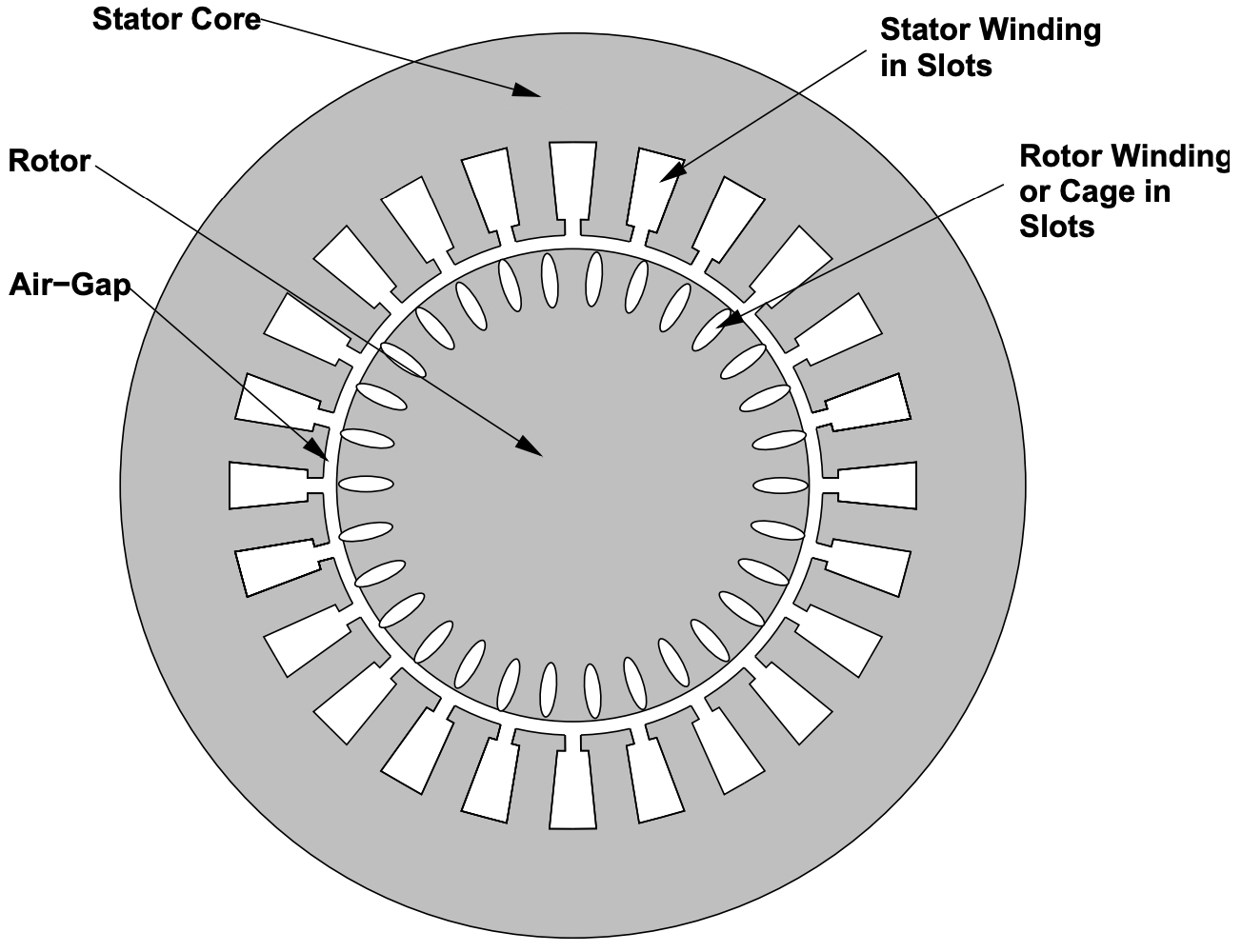    Screen Shot 2021-07-23 a las 5.13.34 PM.pngFigura 1: Vista axial de una máquina de inducción

    This page titled 10: Evaluación analítica del diseño de máquinas de inducción is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by James Kirtley (MIT OpenCourseWare) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.