12.7: Maquetación

La geometría asumida se muestra en la Figura 11. Se supone que los límites de hierro (altamente permeables) están en radios\(\ R_{i}\) y\(\ R_{s}\). Los imanes permanentes, que se supone que están polarizados radial y alternativamente (es decir, Norte-Sur...), se encuentran entre radios\(\ R_{1}\) y\(\ R_{2}\). Suponemos que hay pares de\(\ p\) polos (\(\ 2 p\)imanes) y que cada imán subsume un ángulo eléctrico de\(\ \theta_{m e}\). El ángulo eléctrico es solo\(\ p\) veces el ángulo físico, de modo que si el ángulo del imán fuera\(\ \theta_{m e}=\pi\), los imanes estarían tocando.

Si los imanes están dispuestos de manera que los imanes polarizados radialmente se localicen alrededor del origen azimutal\(\ (\theta=0)\), el espacio fundamental de la magnetización es:

\[\ \bar{M}=\bar{i}_{r} M_{0} \cos p \theta\tag{41} \]

donde la magnitud fundamental es:

\[\ M_{0}=\frac{4}{\pi} \sin \frac{\theta_{m e}}{2} \frac{B_{\mathrm{rem}}}{\mu_{0}}\tag{42} \]

y\(\ B_{\text {rem }}\) es la magnetización remanente del imán permanente.

Dado que no hay corriente en ninguna parte de este problema, es conveniente tratar el campo magnético como el gradiente de un potencial escalar:

\[\ \bar{H}=-\nabla \psi\tag{43} \]

La divergencia de esto es:

\[\ \nabla^{2} \psi=-\nabla \cdot \bar{H}\tag{44} \]

Dado que la densidad de flujo magnético está libre de divergencias,

\[\ \nabla \cdot \bar{B}=0\tag{45} \]

contamos con:

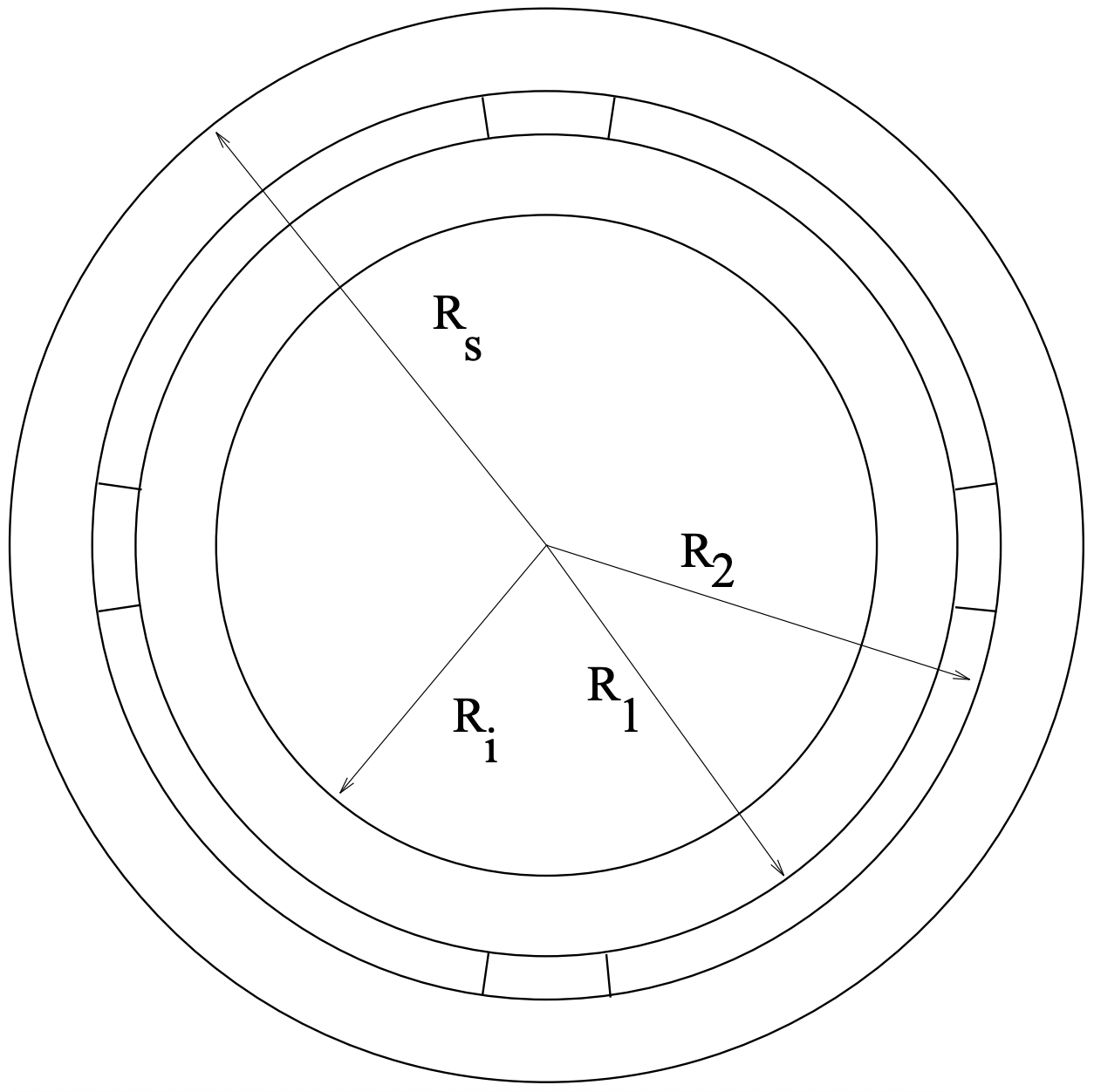Figura 11: Vista axial del problema del campo magnético

\[\ \nabla \cdot \bar{H}=-\nabla \cdot \bar{M}\tag{46} \]

o:

\[\ \nabla^{2} \psi=\nabla \cdot \bar{M}=\frac{1}{r} M_{0} \cos p \theta\tag{47} \]

Ahora bien, si dejamos que el potencial escalar magnético sea la suma de partes particulares y homogéneas:

\[\ \psi=\psi_{p}+\psi_{h}\tag{48} \]

donde\(\ \nabla^{2} \psi_{h}=0\), entonces:

\[\ \nabla^{2} \psi_{p}=\frac{1}{r} M_{0} \cos p \theta\tag{49} \]

Podemos encontrar una solución adecuada a la parte particular de esto en la región de la magnetización intentando:

\[\ \psi_{p}=C r^{\gamma} \cos p \theta\tag{50} \]

Llevando a cabo el Laplaciano sobre esto:

\[\ \nabla^{2} \psi_{p}=C r^{\gamma-2}\left(\gamma^{2}-p^{2}\right) \cos p \theta=\frac{1}{r} M_{0} \cos p \theta\tag{51} \]

que funciona si\(\ \gamma=1\), en cuyo caso:

\[\ \psi_{p}=\frac{M_{0} r}{1-p^{2}} \cos p \theta\tag{52} \]

Por supuesto, esta solución se mantiene solo para la región de los imanes:\(\ R_{1}<r<R_{2}\), y es cero para las regiones fuera de los imanes.

Una solución homogénea adecuada satisface la ecuación de Laplace\(\ \nabla^{2} \psi_{h}=0\), y es en general de la forma:

\[\ \psi_{h}=A r^{p} \cos p \theta+B r^{-p} \cos p \theta\tag{53} \]

Entonces podemos escribir una solución total de prueba para la densidad de flujo como:

\[\ R_{i}<r<R_{1} \quad \psi=\left(A_{1} r^{p}+B_{1} r^{-p}\right) \cos p \theta\tag{54} \]

\[\ R_{1}<r<R_{2} \quad \psi=\left(A_{2} r^{p}+B_{2} r^{-p}+\frac{M_{0} r}{1-p^{2}}\right) \cos p \theta\tag{55} \]

\[\ R_{2}<r<R_{s} \quad \psi=\left(A_{3} r^{p}+B_{3} r^{-p}\right) \cos p \theta\tag{56} \]

Las condiciones límite en los límites interno y externo (asumido infinitamente permeables) en\(\ r=R_{i}\) y\(\ r=R_{s}\) requieren que el campo azimutal desaparezca, o\(\ \frac{\partial \psi}{\partial \theta}=0\), conduciendo a:

\[\ B_{1}=-R_{i}^{2 p} A_{1}\tag{57} \]

\[\ B_{3}=-R_{s}^{2 p} A_{3}\tag{58} \]

En los radios interior y exterior del imán,\(\ H_{\theta}\) y\(\ B_{r}\) debe ser continuo. Estos son:

\[\ H_{\theta}=-\frac{1}{r} \frac{\partial \psi}{\partial \theta}\tag{59} \]

\[\ B_{r}=\mu_{0}\left(-\frac{\partial \psi}{\partial r}+M_{r}\right)\tag{60} \]

Estos se convierten, en\(\ r=R_{1}\):

\[\ -p A_{1}\left(R_{1}^{p-1}-R_{i}^{2 p} R_{1}^{-p-1}\right)=-p\left(A_{2} R_{1}^{p-1}+B_{2} R_{1}^{-p-1}\right)-p \frac{M_{0}}{1-p^{2}}\tag{61} \]

\[\ -p A_{1}\left(R_{1}^{p-1}+R_{i}^{2 p} R_{1}^{-p-1}\right)=-p\left(A_{2} R_{1}^{p-1}-B_{2} R_{1}^{-p-1}\right)-\frac{M_{0}}{1-p^{2}}+M_{0}\tag{62} \]

y en\(\ r=R_{2}\):

\[\ -p A_{3}\left(R_{2}^{p-1}-R_{s}^{2 p} R_{2}^{-p-1}\right)=-p\left(A_{2} R_{2}^{p-1}+B_{2} R_{2}^{-p-1}\right)-p \frac{M_{0}}{1-p^{2}}\tag{63} \]

\[\ -p A_{3}\left(R_{2}^{p-1}+R_{s}^{2 p} R_{2}^{-p-1}\right)=-p\left(A_{2} R_{2}^{p-1}-B_{2} R_{2}^{-p-1}\right)-\frac{M_{0}}{1-p^{2}}+M_{0}\tag{64} \]

Algunas pequeñas manipulaciones de estos rendimientos:

\[\ A_{1}\left(R_{1}^{p}-R_{i}^{2 p} R_{1}^{-p}\right)=A_{2} R_{1}^{p}+B_{2} R_{1}^{-p}+R_{1} \frac{M_{0}}{1-p^{2}}\tag{65} \]

\[\ A_{1}\left(R_{1}^{p}+R_{i}^{2 p} R_{1}^{-p}\right)=A_{2} R_{1}^{p}-B_{2} R_{1}^{-p}+p R_{1} \frac{M_{0}}{1-p^{2}}\tag{66} \]

\[\ A_{3}\left(R_{2}^{p}-R_{s}^{2 p} R_{2}^{-p}\right)=A_{2} R_{2}^{p}+B_{2} R_{2}^{-p}+R_{2} \frac{M_{0}}{1-p^{2}}\tag{67} \]

\[\ A_{3}\left(R_{2}^{p}+R_{s}^{2 p} R_{2}^{-p}\right)=A_{2} R_{2}^{p}-B_{2} R_{2}^{-p}+p R_{2} \frac{M_{0}}{1-p^{2}}\tag{68} \]

Tomando sumas y diferencias del primero y segundo y luego tercero y cuarto de estos obtenemos:

\[\ 2 A_{1} R_{1}^{p}=2 A_{2} R_{1}^{p}+R_{1} M_{0} \frac{1+p}{1-p^{2}}\tag{69} \]

\[\ 2 A_{1} R_{i}^{2 p} R_{1}^{-p}=-2 B_{2} R_{1}^{-p}+R_{1} M_{0} \frac{p-1}{1-p^{2}}\tag{70} \]

\[\ 2 A_{3} R_{2}^{p}=2 A_{2} R_{2}^{p}+R_{2} M_{0} \frac{1+p}{1-p^{2}}\tag{71} \]

\[\ 2 A_{3} R_{s}^{2 p} R_{2}^{-p}=-2 B_{2} R_{2}^{-p}+R_{2} M_{0} \frac{p-1}{1-p^{2}}\tag{72} \]

y luego multiplicando por factores apropiados (R2 p y R1 p y luego tomando sumas y diferencias de estos,

\[\ \left(A_{1}-A_{3}\right) R_{1}^{p} R_{2}^{p}=\left(R_{1} R_{2}^{p}-R_{2} R_{1}^{p}\right) \frac{M_{0}}{2} \frac{p+1}{1-p^{2}}\tag{73} \]

\[\ \left(A_{1} R_{i}^{2 p}-A_{3} R_{s}^{2 p}\right) R_{1}^{-p} R_{2}^{-p}=\left(R_{1} R_{2}^{-p}-R_{2} R_{1}^{-p}\right) \frac{M_{0}}{2} \frac{p-1}{1-p^{2}}\tag{74} \]

Dividiendo por los grupos apropiados:

\[\ A_{1}-A_{3}=\frac{R_{1} R_{2}^{p}-R_{2} R_{1}^{p}}{R_{1}^{p} R_{2}^{p}} \frac{M_{0}}{2} \frac{1+p}{1-p^{2}}\tag{75} \]

\[\ A_{1} R_{i}^{2 p}-A_{3} R_{s}^{2 p}=\frac{R_{1} R_{2}^{-p}-R_{2} R_{1}^{-p}}{R_{1}^{-p} R_{2}^{-p}} \frac{M_{0}}{2} \frac{p-1}{1-p^{2}}\tag{76} \]

y luego, multiplicando la ecuación superior por\(\ R_{s}^{2 p}\) y restando:

\[\ A_{1}\left(R_{s}^{2 p}-R_{i}^{2 p}\right)=\left(\frac{R_{1} R_{2}^{p}-R_{2} R_{1}^{p}}{R_{1}^{p} R_{2}^{p}} \frac{M_{0}}{2} \frac{1+p}{1-p^{2}}\right) R_{s}^{2 p}-\frac{R_{1} R_{2}^{-p}-R_{2} R_{1}^{-p}}{R_{1}^{-p} R_{2}^{-p}} \frac{M_{0}}{2} \frac{p-1}{1-p^{2}}\tag{77} \]

Esto se resuelve fácilmente para los coeficientes de campo\(\ A_{1}\) y\(\ A_{3}\):

\[\ A_{1}=-\frac{M_{0}}{2\left(R_{s}^{2 p}-R_{i}^{2 p}\right)}\left(\frac{p+1}{p^{2}-1}\left(R_{1}^{1-p}-R_{2}^{1-p}\right) R_{s}^{2 p}+\frac{p-1}{p^{2}-1}\left(R_{2}^{1+p}-R_{1}^{1+p}\right)\right)\tag{78} \]

\[\ A_{3}=-\frac{M_{0}}{2\left(R_{s}^{2 p}-R_{i}^{2 p}\right)}\left(\frac{1}{1-p}\left(R_{1}^{1-p}-R_{2}^{1-p}\right) R_{i}^{2 p}-\frac{1}{1+p}\left(R_{2}^{1+p}-R_{1}^{1+p}\right)\right)\tag{79} \]

Ahora, señalando que el potencial escalar es, en la región 1 (radios menores que el imán),

\(\ \psi=A_{1}\left(r^{p}-R_{i}^{2 p} r^{-p}\right) \cos p \theta \quad r<R_{1}\)

\(\ \psi=A_{3}\left(r^{p}-R_{s}^{2 p} r^{-p}\right) \cos p \theta \quad r>R_{2}\)

y señalando que\(\ p(p+1) /\left(p^{2}-1\right)=p /(p-1)\) y\(\ p(p-1) /\left(p^{2}-1\right)=p /(p+1)\), el campo magnético es

\ (\ 80\ begin {alineado}
& r<r_ {1}\
H_ {r} =&\ frac {M_ {0}} {2\ left (R_ {s} ^ {2 p} -R_ {i} ^ {2 p}\ derecha)}\ izquierda (\ frac {p} {p-1}\ izquierda (R_ {1} ^ {1-p} -R_ {2} ^ {1-p}\ derecha) R_ {s} ^ {2 p} +\ frac {p} {p+1}\ izquierda (R_ {2} ^ {1+p} -R_ {1} ^ {1+p}\ derecha)\ derecha)\ izquierda (r^ {p-1} +R_ {i} ^ {2 p} r^ {-p-1}\ derecha)\ cos p\ theta \\
& R>r_ {2}
\ final {alineado}\)

\ [\\ begin {alineado}
& r<r_ {1}\
H_ {r} =&\ frac {M_ {0}} {2\ left (R_ {s} ^ {2 p} -R_ {i} ^ {2 p}\ derecha)}\ izquierda (\ frac {p} {p-1}\ izquierda (R_ {1} ^ {1-p} -R_ {2} ^ {1-p}\ derecha) R_ {s} ^ {2 p} +\ frac {p} {p+1}\ izquierda (R_ {2} ^ {1+p} -R_ {1} ^ {1+p}\ derecha)\ derecha)\ izquierda (r^ {p-1} +R_ {i} ^ {2 p} r^ {-p-1}\ derecha)\ cos p theta\ \
& r>r_ {2}
\ end {alineado}\ tag {80}\]

\[\ H_{r}=\frac{M_{0}}{2\left(R_{s}^{2 p}-R_{i}^{2 p}\right)}\left(\frac{p}{p-1}\left(R_{1}^{1-p}-R_{2}^{1-p}\right) R_{i}^{2 p}+\frac{p}{p+1}\left(R_{2}^{1+p}-R_{1}^{1+p}\right)\right)\left(r^{p-1}+R_{s}^{2 p} r^{-p-1}\right) \cos p \theta\tag{81} \]

El caso de\(\ p=1\) parece ser un poco problemático aquí, pero se maneja fácilmente al señalar que:

\(\ \lim _{p \rightarrow 1} \frac{p}{p-1}\left(R_{1}^{1-p}-R_{2}^{1-p}\right)=\log \frac{R_{2}}{R_{1}}\)

Ahora: hay una serie de casos especiales a considerar.

Para el estuche sin hierro,\(\ R_{i} \rightarrow 0\) y\(\ R_{2} \rightarrow \infty\), esto se convierte, simplemente, para\(\ r<R_{1}\)

\[\ H_{r}=\frac{M_{0}}{2} \frac{p}{p-1}\left(R_{1}^{1-p}-R_{2}^{1-p}\right) r^{p-1} \cos p \theta\tag{82} \]

Tenga en cuenta que para el caso de\(\ p=1\), el límite de esto es

\(\ H_{r}=\frac{M_{0}}{2} \log \frac{R_{2}}{R_{1}} \cos \theta\)

y para\(\ r>R_{2}\):

\(\ H_{r}=\frac{M_{0}}{2} \frac{p}{p+1}\left(R_{2}^{p+1}-R_{1}^{p+1}\right) r^{-(p+1)} \cos p \theta\)

Para el caso de una máquina con límites de hierro y devanados en ranuras, nos interesan los campos en los límites. En tal caso, generalmente, ya sea\(\ R_{i}=R_{1}\) o\(\ R_{s}=R_{2}\). Los campos son:

en el límite exterior\(\ r=R_{s}\):

\(\ H_{r}=M_{0} \frac{R_{s}^{p-1}}{R_{s}^{2 p}-R_{i}^{2 p}}\left(\frac{p}{p+1}\left(R_{2}^{p+1}-R_{1}^{p+1}\right)+\frac{p}{p-1} R_{i}^{2 p}\left(R_{1}^{1-p}-R_{2}^{1-p}\right)\right) \cos p \theta\)

o en el límite interior\(\ r=R_{i}\):

\(\ H_{r}=M_{0} \frac{R_{i}^{p-1}}{R_{s}^{2 p}-R_{i}^{2 p}}\left(\frac{p}{p+1}\left(R_{2}^{p+1}-R_{1}^{p+1}\right)+\frac{p}{p-1} R_{s}^{2 p}\left(R_{1}^{1-p}-R_{2}^{1-p}\right)\right) \cos p \theta\)