3.1: Teorema de Poynting
- Page ID
- 83856
A pesar de la aparente complejidad de la teoría electromagnética, de hecho no hay más que cuatro formas de manipular la energía electromagnética. La energía electromagnética puede ser:
- Transferidos; es decir, transportados por líneas de transmisión o en ondas;
- Almacenado en un campo eléctrico (capacitancia);
- Almacenado en un campo magnético (inductancia); o
- Disipado (convertido a calor; es decir, resistencia).
El teorema de Poynting es una expresión de conservación de energía que relaciona elegantemente estas diversas posibilidades. Una vez reconocido, el teorema tiene importantes aplicaciones en el análisis y diseño de sistemas electromagnéticos. Algunos de estos surgen de la derivación del teorema, a diferencia del resultado no sorprendente. Entonces, derivemos ahora el teorema.
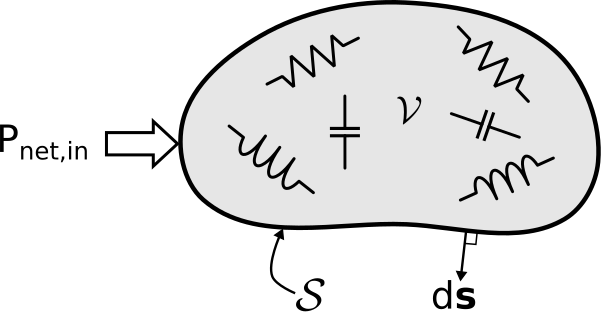
Comenzamos con una declaración del teorema. Considere un volumen\(\mathcal{V}\) que pueda contener materiales y estructuras en cualquier combinación. Esto se representa groseramente en la Figura\(\PageIndex{1}\).
También recordemos que el poder es la tasa de tiempo de cambio de la energía. Entonces:
\[P_{net,in} = P_E + P_M + P_{\Omega} \label{m0073_ePTa} \]
donde\(P_{net,in}\) es el flujo de energía neta\(\mathcal{V}\),\(P_E\) es la potencia asociada con el almacenamiento de energía en los campos eléctricos dentro\(\mathcal{V}\),\(P_M\) es la potencia asociada con el almacenamiento de energía en los campos magnéticos dentro\(\mathcal{V}\), y\(P_{\Omega}\) es la potencia disipada (convertida en calor) en \(\mathcal{V}\).
Algunos resultados matemáticos preliminares
Ahora derivamos dos relaciones matemáticas que serán útiles posteriormente. Dejar\({\bf E}\) ser la intensidad del campo eléctrico (unidades base SI de V/m) y dejar\({\bf D}\) ser la densidad de flujo eléctrico (unidades base SI de C/m\(^2\)). Requerimos que los constituyentes de\(\mathcal{V}\) sean lineales e invariables en el tiempo; por lo tanto,\({\bf D}=\epsilon{\bf E}\) donde la permitividad\(\epsilon\) es constante con respecto al tiempo, pero no necesariamente con respecto a la posición. Bajo estas condiciones, encontramos
\[\frac{\partial}{\partial t} \left( {\bf E}\cdot{\bf D} \right) = \frac{1}{\epsilon} \frac{\partial}{\partial t} \left( {\bf D}\cdot{\bf D} \right) %\label{m0073_ePTp2a} \]
Obsérvese eso\({\bf E}\) y\({\bf D}\) apunte en la misma dirección. Dejado\(\hat{\bf e}\) ser el vector de unidad que describe esta dirección. Entonces,\({\bf E}=\hat{\bf e}E\) y\({\bf D}=\hat{\bf e}D\) dónde\(E\) y\(D\) son los componentes escalares de\({\bf E}\) y\({\bf D}\), respectivamente. Posteriormente,
\[\begin{aligned} \frac{1}{\epsilon} \frac{\partial}{\partial t} \left( {\bf D}\cdot{\bf D} \right) &= \frac{1}{\epsilon} \frac{\partial}{\partial t} D^2 \nonumber \\ &= \frac{1}{\epsilon} 2D \frac{\partial}{\partial t} D \nonumber \\ &= 2 {\bf E} \cdot \frac{\partial}{\partial t} {\bf D} \end{aligned} \nonumber \]
Resumiendo:
\[\frac{\partial}{\partial t} \left( {\bf E}\cdot{\bf D} \right) = 2 {\bf E} \cdot \frac{\partial}{\partial t} {\bf D} \label{m0073_ePTp2} \]
que es la expresión que buscamos. Cabe señalar que las expresiones en ambos lados de la ecuación tienen las mismas unidades, es decir, las de poder.
Usando el mismo razonamiento, encontramos:
\[\frac{\partial}{\partial t} \left( {\bf H}\cdot{\bf B} \right) = 2 {\bf H} \cdot \frac{\partial}{\partial t} {\bf B} \label{m0073_ePTp3} \]
donde\({\bf H}\) es la intensidad del campo magnético (unidades base SI de A/m) y\({\bf B}\) es la densidad de flujo magnético (unidades base SI de T).
Derivación del Teorema
Comenzamos con la forma diferencial de la ley de Ampere:
\[\nabla \times {\bf H} = {\bf J} + \frac{\partial}{\partial t}{\bf D} \nonumber \]
Tomando el producto punteado con\({\bf E}\) en ambos lados:
\[{\bf E} \cdot \left( \nabla \times {\bf H} \right) = {\bf E} \cdot {\bf J} + {\bf E} \cdot \frac{\partial}{\partial t}{\bf D} \label{m0073_ePTp3a} \]
Tratemos primero con el lado izquierdo de esta ecuación. Para ello, emplearemos una identidad vectorial del Apéndice B.3:
\[ \nabla \cdot(\mathbf{A} \times \mathbf{B})=\mathbf{B} \cdot(\nabla \times \mathbf{A})-\mathbf{A} \cdot(\nabla \times \mathbf{B}) \nonumber \]
Esta identidad establece que para dos campos vectoriales cualesquiera\({\bf F}\) y\({\bf G}\),
\[\nabla \cdot \left( {\bf F} \times {\bf G} \right) = {\bf G} \cdot \left( \nabla \times {\bf F} \right) - {\bf F} \cdot \left( \nabla \times {\bf G} \right) \nonumber \]
Sustituyendo\({\bf E}\)\({\bf F}\)\({\bf G}\) y\({\bf H}\) reordenando términos, encontramos
\[{\bf E} \cdot \left( \nabla \times {\bf H} \right) = {\bf H} \cdot \left( \nabla \times {\bf E} \right) - \nabla \cdot \left( {\bf E} \times {\bf H} \right) \label{m0073_ePTp4} \]
A continuación, invocamos la ecuación de Maxwell-Faraday:
\[\nabla \times {\bf E} = -\frac{\partial}{\partial t}{\bf B} \nonumber \]
Usando esta ecuación para reemplazar el factor entre paréntesis en el segundo término de la Ecuación\ ref {M0073_EPTP4}, obtenemos:
\[{\bf E} \cdot \left( \nabla \times {\bf H} \right) = {\bf H} \cdot \left( -\frac{\partial}{\partial t}{\bf B} \right) - \nabla \cdot \left( {\bf E} \times {\bf H} \right) \nonumber \]
Sustituyendo esta expresión por el lado izquierdo de la Ecuación\ ref {M0073_EPTP3a}, tenemos
\[- {\bf H} \cdot \frac{\partial}{\partial t}{\bf B} - \nabla \cdot \left( {\bf E} \times {\bf H} \right) = {\bf E} \cdot {\bf J} + {\bf E} \cdot \frac{\partial}{\partial t} {\bf D} \nonumber \]
A continuación invocamos las identidades de Ecuaciones\ ref {M0073_EPTP2} y\ ref {M0073_EPTP3} para reemplazar los términos primero y último:
\[\begin{aligned} - \frac{1}{2} \frac{\partial}{\partial t} \left( {\bf H}\cdot{\bf B} \right) &- \nabla \cdot \left( {\bf E} \times {\bf H} \right) \nonumber \\ &= {\bf E} \cdot {\bf J} + \frac{1}{2} \frac{\partial}{\partial t} \left( {\bf E}\cdot{\bf D} \right)\end{aligned} \nonumber \]
Ahora movemos el primer término al lado derecho e integramos ambos lados sobre el volumen\(\mathcal{V}\):
\[\begin{aligned} - \int_{\mathcal{V}} &\nabla \cdot \left( {\bf E} \times {\bf H} \right) dv \nonumber \\ &= \int_{\mathcal{V}} {\bf E} \cdot {\bf J}~dv \nonumber \\ &+ \int_{\mathcal{V}} \frac{1}{2} \frac{\partial}{\partial t} \left( {\bf E}\cdot{\bf D} \right) dv \nonumber \\ &+ \int_{\mathcal{V}} \frac{1}{2} \frac{\partial}{\partial t} \left( {\bf H}\cdot{\bf B} \right) dv\end{aligned} \nonumber \]
El lado izquierdo puede transformarse en una integral de superficie usando el teorema de divergencia:
\[\int_{\mathcal{V}} \nabla \cdot \left( {\bf E} \times {\bf H} \right) dv = \oint_{\mathcal{S}} \left( {\bf E} \times {\bf H} \right) \cdot d{\bf s} \nonumber \]
donde\(\mathcal{S}\) está la superficie cerrada que limita\(\mathcal{V}\) y\(d{\bf s}\) es la normal orientada hacia afuera a esta superficie, como se indica en la Figura\(\PageIndex{1}\). Finalmente, intercambiamos el orden de diferenciación temporal e integración de volúmenes en los dos últimos términos:
\[\begin{align} - \oint_{\mathcal{S}} &\left( {\bf E} \times {\bf H} \right) \cdot d{\bf s} \nonumber \\ &= \int_{\mathcal{V}} {\bf E} \cdot {\bf J}~dv \nonumber \\ &+ \frac{1}{2}\frac{\partial}{\partial t} \int_{\mathcal{V}} {\bf E}\cdot{\bf D}~dv \nonumber \\ &+ \frac{1}{2}\frac{\partial}{\partial t} \int_{\mathcal{V}} {\bf H}\cdot{\bf B}~dv \label{m0073_ePTi}\end{align} \]
La ecuación\ ref {M0073_epti} es el teorema de Poynting. Cada uno de los cuatro términos tiene la interpretación física particular identificada en la Ecuación\ ref {M0073_EPTA}, como ahora demostraremos.
Potencia disipada por pérdida óhmica
El primer término del lado derecho de la ecuación\ ref {M0073_epti} es
\[\boxed{ P_{\Omega} \triangleq \int_{\mathcal{V}} {\bf E} \cdot {\bf J}~dv } \label{m0073_eJL} \]
La ecuación\ ref {M0073_EJL} es la ley de Joule. La ley de Joule da la potencia disipada debido a la conductividad finita del material. El papel de la conductividad (\(\sigma\), unidades base SI de S/m) se puede hacer explícito usando la relación\({\bf J} = \sigma{\bf E}\) (ley de Ohm) en la Ecuación\ ref {M0073_EJL}, que produce:
\[P_{\Omega} = \int_{\mathcal{V}} {\bf E} \cdot \sigma {\bf E}~dv = \int_{\mathcal{V}} \sigma \left|{\bf E}\right|^2~dv \nonumber \]
\(P_{\Omega}\)se debe a la conversión del campo eléctrico en corriente de conducción, y posteriormente en calor. Este mecanismo se conoce comúnmente como pérdida óhmica o calentamiento por joule. Es de destacar que esta expresión tiene las unidades esperadas. Por ejemplo, en la Ecuación\ ref {M0073_EJL},\({\bf E}\) (unidades base SI de V/m) veces\({\bf J}\) (unidades base SI de A/m\(^2\)) produce una cantidad con unidades de W/m\(^3\); es decir, potencia por unidad de volumen, que es densidad de potencia. Entonces la integración sobre volumen produce unidades de W; de ahí, potencia.
El segundo término en el lado derecho de la ecuación\ ref {M0073_epti} es:
\[\boxed{ P_E \triangleq \frac{1}{2} \frac{\partial}{\partial t} \int_{\mathcal{V}} {\bf E}\cdot{\bf D}~dv } \label{m0073_ePE} \]
Recordemos\({\bf D}=\epsilon{\bf E}\), donde\(\epsilon\) está la permitividad (unidades base SI de F/m) del material. Así, podemos reescribir la ecuación anterior de la siguiente manera:
\[\begin{align} P_E &= \frac{1}{2} \frac{\partial}{\partial t} \int_{\mathcal{V}} {\bf E} \cdot \epsilon {\bf E}~dv \nonumber \\ &= \frac{1}{2} \frac{\partial}{\partial t} \int_{\mathcal{V}} \epsilon \left|{\bf E}\right|^2~dv \nonumber \\ &= \frac{\partial}{\partial t} \left( \frac{1}{2} \int_{\mathcal{V}} \epsilon \left|{\bf E}\right|^2~dv \right)\end{align} \nonumber \]
La cantidad entre paréntesis es\(W_e\), la energía almacenada en el campo eléctrico dentro\(\mathcal{V}\).
El tercer término en el lado derecho de la ecuación\ ref {M0073_epti} es:
\[\boxed{ P_M \triangleq \frac{1}{2} \frac{\partial}{\partial t} \int_{\mathcal{V}} {\bf H}\cdot{\bf B}~dv } \label{m0073_ePM} \]
Recordemos\({\bf B}=\mu{\bf H}\), donde\(\mu\) está la permeabilidad (unidades base SI de H/m) del material. Así, podemos reescribir la ecuación anterior de la siguiente manera:
\[\begin{align} P_M &= \frac{1}{2} \frac{\partial}{\partial t} \int_{\mathcal{V}} {\bf H} \cdot \mu {\bf H}~dv \nonumber \\ &= \frac{1}{2} \frac{\partial}{\partial t} \int_{\mathcal{V}} \mu \left|{\bf H}\right|^2~dv \nonumber \\ &= \frac{\partial}{\partial t} \left( \frac{1}{2} \int_{\mathcal{V}} \mu \left|{\bf H}\right|^2~dv \right)\end{align} \nonumber \]
La cantidad entre paréntesis es\(W_m\), la energía almacenada en el campo magnético dentro\(\mathcal{V}\).
Flujo de potencia a través\(\mathcal{S}\)
El lado izquierdo de la Ecuación\ ref {M0073_EPTi} es
\[\boxed{ P_{net,in} \triangleq -\oint_{\mathcal{S}} \left( {\bf E} \times {\bf H} \right) \cdot d{\bf s} } \label{m0073_ePF} \]
La cantidad\({\bf E} \times {\bf H}\) es el vector Poynting, que cuantifica la densidad de potencia espacial (unidades base SI de W/m\(^2\)) de una onda electromagnética y la dirección en la que se propaga. Es probable que el lector ya se haya encontrado con este concepto. Independientemente, confirmaremos esta interpretación de la cantidad\({\bf E} \times {\bf H}\) en la Sección 3.2. Por ahora, observe que la integración del vector Poynting sobre\(\mathcal{S}\) como se indica en la Ecuación\ ref {M0073_EPF} produce la potencia total que fluye fuera de\(\mathcal{V}\) través\(\mathcal{S}\). El signo negativo en la Ecuación\ ref {M0073_EPF} indica que la cantidad combinada representa el flujo de potencia de entrada a\(\mathcal{V}\) través\(\mathcal{S}\). Finalmente, tenga en cuenta que el uso de una sola cantidad\(P_{net,in}\) no implica que el poder esté completamente dirigido hacia adentro o hacia afuera. Más bien,\(P_{net,in}\) representa el flujo neto; es decir, la suma de la potencia que fluye hacia adentro y hacia afuera.
Resumen. La ecuación\ ref {M0073_epti} ahora se puede establecer de manera concisa de la siguiente manera:
\[\boxed{ P_{net,in} = P_{\Omega} + \frac{\partial}{\partial t}W_e + \frac{\partial}{\partial t}W_m } \label{m0073_ePT} \]
El teorema de Poynting (Ecuación\ ref {M0073_EPT}, con Ecuaciones\ ref {M0073_EPF},\ ref {M0073_eJL},\ ref {M0073_EPE}, y\ ref {M0073_EPM}) establece que la potencia electromagnética neta que fluye hacia una región del espacio puede ser disipada, o utilizada para cambiar la energía almacenada en electricidad y campos magnéticos dentro de ese región.
Dado que derivamos este resultado directamente de la forma general de las ecuaciones de Maxwell, estas tres posibilidades son todas las posibilidades permitidas por la física clásica, por lo que esta es una declaración de conservación del poder.
Finalmente, tenga en cuenta que el teorema también funciona a la inversa; es decir, la potencia electromagnética neta que fluye fuera de una región del espacio debe haberse originado a partir de alguna fuente activa (es decir, la inversa de la disipación de potencia) o liberada de la energía almacenada en campos eléctricos o magnéticos.
Lectura adicional:
- “Poynting vector” en Wikipedia.


