5.4: Propagación de una onda plana uniforme en una dirección arbitraria
- Page ID
- 83765
En la Figura se muestra un ejemplo de una onda plana uniforme que se propaga en un medio sin pérdidas\(\PageIndex{1}\).
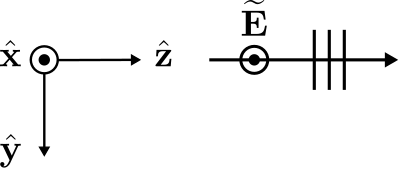
Esta onda se expresa en el sistema de coordenadas indicado de la siguiente manera:
\[\widetilde{\bf E} = \hat{\bf x} E_0 e^{-j\beta z} \label{m0165_eEx} \]
Esta es una expresión de dominio de fase para la intensidad del campo eléctrico, por lo que\(E_0\) es un número de valor complejo que representa la magnitud y la fase de referencia de la onda sinusoidalmente variable. El término “fase de referencia” se define como la fase de\(\widetilde{\bf E}\) en el origen del sistema de coordenadas. Dado que la constante de propagación de fase\(\beta\) es real y positiva, esta onda viaja en la\(+\hat{\bf z}\) dirección a través de medios simples sin pérdidas.
Tenga en cuenta que el vector de intensidad de campo eléctrico está polarizado linealmente en una dirección paralela a\(\hat{\bf x}\). Dependiendo de la posición en el espacio (y, para la forma de onda física en el dominio del tiempo, el tiempo),\(\widetilde{\bf E}\) apunta ya sea en la\(+\hat{\bf x}\) dirección o en la\(-\hat{\bf x}\) dirección. Seamos un poco más específicos sobre la dirección del vector\(\widetilde{\bf E}\). Para ello, definamos la polarización de referencia como la dirección en la que\(\widetilde{\bf E}\) apunta cuándo\(\mbox{Re}\left\{E_0 e^{-j\beta z}\right\}\ge 0\); es decir, cuando la fase de\(\widetilde{\bf E}\) está entre\(-\pi/2\) y\(+\pi/2\) radianes. Así, la polarización de referencia de\(\widetilde{\bf E}\) en la Ecuación\ ref {M0165_Eex} es siempre\(+\hat{\bf x}\).
Tenga en cuenta que la Ecuación\ ref {M0165_Eex} indica una combinación específica de polarización de referencia y dirección de propagación. Sin embargo, podemos obtener cualquier otra combinación de polarización de referencia y dirección de propagación por rotación del sistema de coordenadas cartesianas. Por ejemplo, si giramos el\(+x\) eje del sistema de coordenadas a la posición originalmente ocupada por el\(+y\) eje, entonces la misma onda se expresa como
\[\widetilde{\bf E} = -\hat{\bf y} E_0 e^{-j\beta z} \label{m0165_eEy} \]
Esto se ilustra en la Figura\(\PageIndex{2}\).
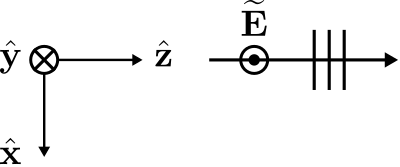
A primera vista, parece que la polarización de referencia ha cambiado; sin embargo, esto se debe enteramente a nuestra elección del sistema de coordenadas. Es decir, la polarización de referencia es precisamente la misma; es sólo el sistema de coordenadas utilizado para describir la polarización de referencia lo que ha cambiado.
Ahora rotemos el\(+z\) eje del sistema de coordenadas alrededor del\(x\) eje hacia la posición originalmente ocupada por el\(-z\) eje. Ahora la misma onda se expresa como
\[\widetilde{\bf E} = +\hat{\bf y} E_0 e^{+j\beta z} \label{m0165_eEz} \]
Esto se ilustra en la Figura\(\PageIndex{3}\).
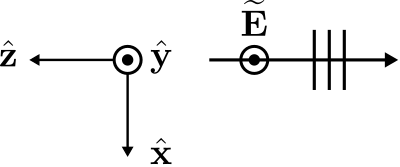
A primera vista, parece que la dirección de propagación se ha invertido; pero, nuevamente, es sólo el sistema de coordenadas el que ha cambiado, y no la dirección de propagación. Resumiendo: Ecuaciones\ ref {M0165_Eex},\ ref {M0165_eey}, y\ ref {M0165_eez} representan la misma onda. Solo parecen ser diferentes debido a nuestra elección para la orientación del sistema de coordenadas en cada caso.
Consideremos ahora el mismo experimento de pensamiento para el número infinito de casos en los que la onda no se propaga en una de las tres direcciones base del sistema de coordenadas cartesianas. Una situación en la que nos enfrentamos a esta complicación es cuando la ola incide oblicuamente sobre una superficie. En este caso, es imposible seleccionar una sola orientación del sistema de coordenadas en la que las direcciones de propagación, polarización de referencia y normal de superficie puedan describirse en términos de un vector base cada una. Para ser claros: No existe una limitación fundamental impuesta por esta deslizabilidad del sistema de coordenadas. Sin embargo, problemas prácticos como el escenario de oblicuo-incidencia descrito anteriormente son mucho más fáciles de analizar si somos capaces de expresar ondas en un sistema de coordenadas que siempre arroja las mismas expresiones.
Afortunadamente, esto se logra fácilmente usando coordenadas fijas por Ray-Fixed. Las coordenadas fijas por rayo son un conjunto único de coordenadas que se determinan a partir de las características de la onda, en contraposición a ser determinadas arbitrariamente y por separado de las características de la onda. La representación fija de un ray-fijo de una onda plana uniforme es:
\[\boxed{ \widetilde{\bf E}({\bf r}) = \hat{\bf e} E_0 e^{-j{\bf k}\cdot{\bf r}} } \label{m0165_eE} \]
Esto se ilustra en la Figura\(\PageIndex{4}\).
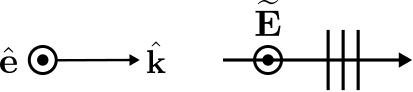
En esta representación,\({\bf r}\) se encuentra la posición en la que\(\widetilde{\bf E}\) se evalúa,\(\hat{\bf e}\) es la polarización de referencia expresada como un vector unitario, y\({\bf k}\) es el vector unitario\(\hat{\bf k}\) en la dirección de propagación, tiempos\(\beta\); es decir:
\[{\bf k} \triangleq \hat{\bf k}\beta \nonumber \]
Considera la Ecuación\ ref {M0165_Eex} como ejemplo. En este caso,\(\hat{\bf e}=\hat{\bf x}\),\({\bf k} = \hat{\bf z}\beta\), y (como siempre)
\[{\bf r} = \hat{\bf x}x +\hat{\bf y}y +\hat{\bf z}z \nonumber \]
Así,\({\bf k}\cdot{\bf r}=\beta z\), como se esperaba.
En coordenadas fijas por rayo, una onda puede ser representada por una —y sólo una— expresión, que es la misma expresión independientemente de la orientación del sistema de coordenadas “global”. Además, sólo deben definirse dos direcciones básicas (a saber,\(\hat{\bf k}\) y\(\hat{\bf e}\)). Si se requiere una tercera coordenada, ya sea\(\hat{\bf k} \times \hat{\bf e}\) o\(\hat{\bf e} \times \hat{\bf k}\) puede ser seleccionada como la dirección base adicional. Tenga en cuenta que la primera opción tiene la característica posiblemente útil que es la polarización de referencia de la intensidad del campo magnético\(\widetilde{\bf H}\).
Un procedimiento general para refundir la representación fija por rayo en una representación “coordinada” es el siguiente. Primero, representamos\({\bf k}\) en el nuevo sistema de coordenadas fijas; por ejemplo:
\[{\bf k} = k_x\hat{\bf x} + k_y\hat{\bf y} + k_z\hat{\bf z} \nonumber \]
donde
\[\begin{aligned} k_x &\triangleq \beta\hat{\bf k}\cdot\hat{\bf x} \\ k_y &\triangleq \beta\hat{\bf k}\cdot\hat{\bf y} \\ k_z &\triangleq \beta\hat{\bf k}\cdot\hat{\bf z}\end{aligned} \nonumber \]
Entonces,
\[{\bf k}\cdot{\bf r} = k_x x + k_y y + k_z z \nonumber \]
Con esta expresión en la mano, la Ecuación\ ref {M0165_EE} puede ser reescrita como:
\[\widetilde{\bf E} = \hat{\bf e} E_0 e^{-jk_x x} e^{-jk_y y} e^{-jk_z z} \nonumber \]
Si se desea, uno puede descomponerse de manera similar\(\hat{\bf e}\) en sus componentes cartesianos de la siguiente manera:
\[\hat{\bf e} = \left(\hat{\bf e}\cdot\hat{\bf x}\right)\hat{\bf x} + \left(\hat{\bf e}\cdot\hat{\bf y}\right)\hat{\bf y} + \left(\hat{\bf e}\cdot\hat{\bf z}\right)\hat{\bf z} \nonumber \]
Así, vemos que la representación fija de rayo de la Ecuación\ ref {M0165_EE} acomoda todas las combinaciones posibles de dirección de propagación y polarización de referencia.
Una onda plana uniforme que exhibe una polarización de referencia de\(\hat{\bf z}\) se propaga lejos del\(z\) eje. Desarrollar representaciones de esta onda en coordenadas cartesianas globales y fijas de radios.
Solución
Como siempre, la representación ray-fixed viene dada por la Ecuación\ ref {M0165_EE}. Dado que la polarización de referencia es\(\hat{\bf z}\),\(\hat{\bf e}=\hat{\bf z}\). Propagarse lejos de las medias\(z\) del eje
\[\hat{\bf k} = \hat{\bf x}\cos\phi + \hat{\bf y}\sin\phi \nonumber \]
donde\(\phi\) indica la dirección específica de propagación. Por ejemplo,\(\phi=0\) rendimientos\(\hat{\bf k}=+\hat{\bf x}\),\(\phi=\pi/2\) rendimientos\(\hat{\bf k}=+\hat{\bf y}\), y así sucesivamente. Por lo tanto,
\[{\bf k} \triangleq \beta\hat{\bf k} = \beta\left( \hat{\bf x}\cos\phi + \hat{\bf y}\sin\phi \right) \nonumber \]
Para completarlo, tenga en cuenta que el siguiente factor aparece en el exponente determinante de fase en la Ecuación\ ref {M0165_EE}:
\[{\bf k}\cdot{\bf r} = \beta\left( x\cos\phi + y\sin\phi \right) \nonumber \]
En este caso, vemos\(k_x=\beta \cos\phi\),\(k_y=\beta \sin\phi\), y\(k_z=0\). Así, la onda puede expresarse en coordenadas cartesianas de la siguiente manera:
\[\widetilde{\bf E} = \hat{\bf z} E_0 e^{-j\beta x \cos\phi} e^{-j\beta y \sin\phi} \nonumber \]


